 或
或
話說早在柏拉圖時代(Plato 427~347 B.C.古希臘)就已將正多面體研究得透、透、透,當時對於「平面上有無限多個正多邊形,到了立體空間卻只剩下五個正多面體」這個意外,雖不願相信,卻不得不接受,最後只好搬出「天意」來說服自己承認這個事實。為什麼會從無限多個跳到五個?而且不多不少就是五個?原來,天上的行星也剛剛好只有五個(註1),因此,這五個正多面體就分別代表那五顆行星,而他們的關係便是行星間運行的規則。沒錯,「五個」一定是上帝的旨意!
傳到阿基米得時(Archimedes 287~212 B.C.古希臘),對於三度空間的認識總覺得像是隔靴搔癢,「天意」雖不可違,但總可以變吧!乃將條件鬆綁(註2),又變化出十三個規則的半正多面體,這下可真夠數學家們研究好一陣子了。奇怪的是,對於繁雜的面積、體積、對角線…這等有深度的「算算看」的數學,大家爭相研究、計算,反而最簡單的、幼稚園才會的「數數看」的數學,等了近兩千年,瑞士數學家尤拉(Euler 1707~1783)才發現多面體較基本的點、線、面的數量關係:V – E + F = 2 。千百年來,這條漏網「鯨」魚擋在前頭竟無人聞問,奇哉!怪哉!(註3)
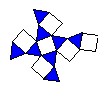
今年給一升二一份暑假作業:多面體製作。發給學生立體的展開圖與平面透視圖,但不指定製作方式與材質,只要求開學後每組(三人)能看到18個立體。終於,蟬鳴聲已噤,只看到多數學生苦笑(做了失敗、做好壓壞),有的傻笑(根本還沒動工),只有少數沒「ㄎ一 ㄒ一ㄠˋ」。交來的心得也多是「E Q管理」的最佳典範,然而其中一位「土尤拉」的發現則是雖不中,亦不遠矣!
心 得 與 發 現
景興國中11班8號 彭于晏
這個暑假數學老師出的作業,可說是把我們給弄瘋了啦
花了好大的功夫才給他做好,而且還有些「ㄌ一ˇㄌ一˙ ㄌㄚˋ ㄌㄚ˙」,不過發現了不少!!
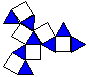
以下是土學生,土土的發現:(一)我們發現到多面體都是由偶數個面組成。(只要數一數就很容易發現的啦!)(二)舉例子說明:正方體有6個面、12個邊、8個角,其他多面體也算出有幾個面、邊、角,統整發現,其中有一個規律,那就是有2N個面、4N個角、6N個邊。(三)將邊數 ×面數 =12的倍數,例如展開圖K(註4),四邊形 ×6個= 24;六邊形 ×8個 = 48,24 + 48 =「72」 12的倍數,其他如此類推。沒錯,就是這些怪怪的發現(應說是頭腦簡單的白痴答案吧!)。
這次作業可要感謝其他2位共同努力的同學,才能完成,老師出的作業雖然煩人,但也讓我們體悟到「知易行難」的道理!!
分析學生的發現,雖有錯誤(註5),但方向卻與尤拉不謀而合。學生已知用N來作一般性公式的假設,若能仔細思量N所扮演的角色,同時搭配更多的數據來驗證或修正自己的發現,相信歷史會重演(當然,「信心」是很重要的:只要數一數就會的發現,哪裡知道竟是個大定理呢!)。從數學史的觀點來看而這樣的「歷史再現」,相信是珍貴而不是浪費。
前人讚嘆:長江後浪推前浪,學生笑接下聯:前浪死在沙灘上;最近又「改良」為:通通死在沙灘上。時代在變、思想在變,人、時、地、事、物都在變,不變的是Σ家常便飯的香與甜!
【註1】當時觀察記載的五顆行星為:水星、金星、(地球)、火星、木星、土星(其他都是恆星)。人類對於天文的觀察與認識,一直要到伽利略發明望遠鏡,才真正大開眼界。刻卜勒曾試圖去觀察、計算各行星的軌道半徑,期與五個正多面體的外接球、中切球或內切球半徑對應,可惜並未成功。
| 多面體 半徑 |
四 |
八 |
六 |
十二 |
二十 |
外接球 |
0.612 |
0.707 |
0.866 |
0.951 |
1.401 |
中切球 |
0.354 |
0.500 |
0.707 |
0.809 |
1.309 |
內切球 |
0.204 |
0.428 |
0.500 |
0.756 |
1.114 |
軌 道 |
0.387 |
0.723 |
1.523 |
5.203 |
9.555 |
| 半徑 行星 |
水星 |
金星 |
火星 |
木星 |
土星 |
各立體球半徑以其多面體邊長為1;各星球軌道半徑以地球為1。若將小行星群與「行星級數」列入考量,結果如下:
| 行星 半徑 |
水星 |
金星 |
地球 |
火星 |
小行星 |
軌道 |
4 |
7 |
10 |
16 |
28 |
虔誠的信徒們不妨嘗試將「多面體邊長為1」改為「多邊形之外接圓半徑或內切圓半徑為1」,或許會出現另一片天空。
【註2】
高中數學統合上冊:多面體與尤拉公式(一)由數個全等的正多邊形組成。
(二)由數種同邊長的正多邊形組成。
(三)每個頂點連接的稜數都相同。
(四)每個立體角皆相等。
滿足條件(一)、(三)、(四)的凸多面體,稱為正多面體,有正四面體、正六面體、正八面體、正十二面體、正二十面體等五種,也通稱為柏拉圖立體;滿足條件(二)、(三)、(四)的凸多面體,稱為半正多面體(semi-regular),有十三種,也通稱為阿基米德立體。後世又將條件(一)放寬為:由數個等邊的多邊形組成,再創造出三種菱形多面體(六、十二、三十),其中菱形六面體有無限多個。
【註3】
稍早,法國的笛卡兒(Descartes 1596~1661)曾發現多面體另一簡單關係式:S = 360度 ×V - 720度(S表示多面體上各多邊形的內角總和)若套用尤拉公式與徑度量Π,上式可變化為:S = 2Π(V - 2)= 2Π(E - F)。【註4】展開圖K :
 或
或

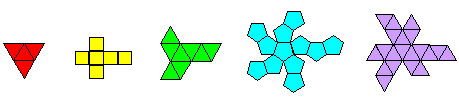
正多面體展開圖:
【註5】(二)應假設為:2a個面、4b個角、6c個邊。進而列表發現:a = b + 1;b = c,再現尤拉公式。(三)應修正為:多邊形A的邊數 ×A在立體上的面數=12的倍數。