在數學各個領域中,由機率得出的結果常有與直覺相衝突之處,亦即用機率算出的正確答案常常相反於常識。例如一個家庭有四個小孩,你會預期最可能的情形是兩男兩女,但這個預期並不正確。又如在一群人中想要找到兩個生日相同者,你也會預期這一群人數要很大量,才會有較高的機率(想像會散在365天之中),但實際只要有23人機率就會大於二分之一,而且會急遽增加,在三十人中兩人同天出生機率已達七成,如果班上超過了35人,你就可以放心的玩打賭遊戲了。
另一個相關學門『統計學』在現今複雜多樣的社會,其地位日趨重要,從各式的普查、到各種資料如地震、股市、交通事故的統計,到處可見統計之用,但相對的,誤導之事也經常發生。常言:數字會說話!但如果聽者不去明辨即亂下因果結論,則產生荒謬可笑之事是可預期的。常見報導如『靠左邊走較不發生事故』、『空運比陸運安全』、『暢銷書都是好書』等,都是值得深思的問題。相關例子可參閱Martin Gardner 所著『Aha! Gotcha』(中文譯本由天下文化出版,書名『跳出思路的陷阱』),該書有更豐富的說明。而相同的情形也發生在機率資料的報導上,像筆者就一直無法理解新聞報導中『下雨機率為40%和60%』有什麼實際的差別及意義。
許多乍聽之下很合理的事情,有時卻不可能發生,而確實正確的理論又有一副讓人難以置信的外表。當尤拉(L.
Euler, 1707-1783)發現
![]() ,即使尤拉本人都感到驚訝。
,即使尤拉本人都感到驚訝。
有一回,狄•摩根(De Morgan, A. 1806-1871)給一位保險計算員講解『一定比例的人在一定時間內仍存活的或然率』,他引用了一個保險計算公式,公式中有一個π,並指出這個π就是圓周與直徑的比。(π、e是機率論中重要的兩個常數,如常態分配的機率密度函數p.d.f 就有π出現。)這個保險統計員本來是濃厚的興趣來聽他解說,聽到這裡卻立刻打斷他,並強烈地說:『親愛的朋友,這一定是個騙局,在一定時間內還存活的人數和圓能有什麼關係?』(De Morgan’s Budget of Paradoxes (London , 1872), p172)
機率論理有個『隨機弦(Random
chord)』問題。考慮一圓的隨機弦長度會超過此圓內接正三角形邊長的機率是多少?這個問題有趣之處,在於如果我們以不同的方向思考隨機弦,將得到不同的答案。例如將隨機弦視為圓上的任意弦,亦即將此弦考慮成圓上隨機兩點P、Q連接而成的弦。接著以P為頂點作一等邊三角形ABP,則當Q落於AB弧之間時,弦PQ會大於等邊三角形ABP邊長。顯而易見地,Q落於AB弧間的機率為1/3。(如圖一)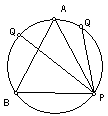
但如果我們將隨機弦用『弦的位置』與『和圓心的距離』來定,此距離可為0到半徑r
的任一隨機值,則當此距離小餘r/2時,弦的長度將大於內接等邊三角形邊長(如圖二),因為內接等邊三角形任一邊到圓心距離為r/2。故機率為P{
d<r/2 }= (r/2) ÷ r = 1/2 。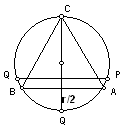
需注意的是,在執行隨機實驗時所求的解1/2和1/3都是正確答案。你或許會感到奇怪,在這麼明確的學門內竟出現這種不定的答案!這原因就在定義的不明確。這說明了什麼奇妙的結果呢?舉個實際的例子,丟一個圓盤到一條直線上,考慮圓盤與線有相交出一弦的情況下,則此弦到圓心所可能的距離機會相等,因此,弦長大於內接等邊三角形邊長的機率為1/2;反之,丟一條線(如一針,想像針的兩邊有無限延伸)到一圓上,同樣地在交出一弦的情況下,所求的機率(弦長大於內接等邊三角形邊長)則變為1/3。
參考資料:
Moritz, R. E. (1914): On Mathematics – A collection of Witty,
Profound, Amusing Passages about Mathematics and
Mathematician, New York.
Ross, S. (1988): A First Course in Probability, third edition , New York.
Martin Gardner(1993):(薛美珍譯)《跳出思路的陷阱》,天下文化。