“我們不要忘記，所謂證明，不只在不同的文化有不同的含意，就連不同的時代也有不同的含意”

臺灣省立新店高中 蘇俊鴻

在實際的教學工作中，無疑地，數學證明的教學是一項頗為艱巨的挑戰！如何將證明過程講解清楚、條理分明是一難；如何生動活潑，吸引學生注目眼光，更是難上加難。事實上，證明的過程正代表著思維的運作，不同的證明方法，表示背後所隱藏的思維模式不同。適當地釐清方法與思維模式的關聯，有助於教師對數學證明的理解與體認。在本文中，則是提供數學史上兩個圓面積公式的證明—由阿基米德(Archimedes，287B.C.?~212B.C.)與劉徽(魏晉，約300A.D.)所提出--分別代表西方數學與中國算學的典型人物。讀者不僅將有一題多証的樂趣，更將有中西文化上差異的發現。

阿基米德對圓的研究記載於《論圓的測量》(On the Measurement of the Circle)的小冊子中，對於圓面積公式，阿基米德的敘述如下：

圓的面積等於以圓半徑及圓周長為兩股的直角三角形面積

劉徽在注解《九章算術》時，提供了圓面積公式的證明，至於圓面積公式，則是記載於《九章算術》（方田）章中的圓田術：

半周半徑相乘得積步

若用今日的數學符號表示，圓半徑= ，圓周長 ，則圓面積= ，兩者的圓面積公式是相同且正確的！接著一起來看看兩人是如何證明，簡略說明如下。解說的過程中，因考慮便利性，在不妨害證明的精神的前提下，輔以適當的現代符號。讓我們先由阿基米德的證明說起。

阿基米德的證明

設 、 分別表示圓面積與直角三角形的面積。阿基米德並不是直接證明 ，而是由 開始。根據三一律，如果 ，則 或 有一種情形將會成立。
(1)若

  如右圖，阿基米德由圓內接正方形開始，接著正八邊形，如此下去，總能找到一個內接正 邊形，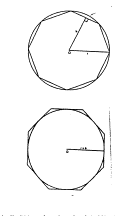

其面積與圓面積的差小於 。設其面積為 ，即

但

這與 的情形發生矛盾，所以 不可能。

(2)若
  如右圖，此次阿基米德由圓的外切正多邊形下手，同上，我們總能找到一個外切正 邊形，

使得它的面積與圓面積的差小於 。設其面積為 ，即

但

這與 的情形發生矛盾，所以 也不可能。

所以，

在這樣間接迂迴的方法中，阿基米德證明了圓面積的公式。接著讓我們一起來看看劉徽的方法吧！

按半周為從，半徑為廣，故廣從相乘為積步也。假令圓徑二尺，圓中容六觚之一面，與圓徑之半，其數均等。合徑率一而弧周率三也。

一開始，劉徽便交待其證明的主要想法是「圓出於方」，在已知正方形面積公式的前提下，證明圓面積公式！並說明π=3是利用圓內接正六邊形所求得的近似值。

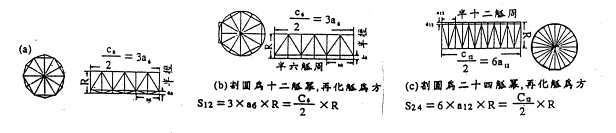
又按為圖，以六觚之一面乘一觚半徑，三之，得十二觚之冪。若又割之，次以十二觚之一面乘一觚之半徑，六之，得二十四觚之冪。割之彌細，所失彌少。割之又割，以至於不可割，則與圓周合體而無所失矣。

接著，劉徽利用「割圓術」，由圓內接正六邊形，分別求出圓內接正十二邊形及正二十四邊形的面積(如下圖)。劉徽進而指出，當切割的動作繼續下去，圓內接正 邊形的面積 與圓面積 的差就愈來愈小。割之又割，到最後圓內接正多邊形便與圓周合為一體！這顯然是一個極限的過程，也就是

觚面之外，猶有餘徑，以面乘餘徑，則冪出弧表。若夫觚之細者，與圓合體，則表無餘徑。表無餘徑，則冪不外出矣。

再來，劉徽說明圓內接正 邊形的每邊 與圓周之間有一餘徑 ，若將各邊長乘上餘徑，其和會大於圓面積，即

                                      然而當 ，則 ，

                                      此時

這表明圓面積 是數列 與 的極限。

以一面乘半徑，觚而裁之，每輒自倍。故以半周乘半徑而為圓冪。此以周、徑，謂至然之數，非周三徑一之率也。

最後，劉徽對與圓周合體的正多邊形進行“無窮分割”，分成無窮多個以正多邊形每邊為底邊 (而圓周長 )，圓心為頂點的小等腰三角形。則小三角形面積 ，則圓面積

就這樣，劉徽就證明了圓面積公式，且明白告訴我們“此以周、徑，謂至然之數，非周三徑一之率也。”

附註：蕭文強寫的《數學證明》一書，值得閱讀，如有興趣，九章出版社有繁體字版。