淺談數學史中的二元一次方程式

長安國中 林倉億老師

    二元一次方程式在數學中是十分基本且重要的概念，下面將對中國、巴比倫和印度數學史中的二元一次方程式做一簡介。由於筆者才疏學淺，資料來源又以中文為主，所以自覺這篇文章有三點不足之處：一、未考量時代背景與數學發展背景。二、未述及解析幾何中的二元一次方程式。三、未述及西方數學對二元一次方程式和二元一次聯立方程式解法的發展。       此外，在收集資料的過程中，發現關於二元一次方程式的資料很少，論及二元一次聯立方程式的更少，猜測這或許與絕大多數的二元一次聯立方程式題目都可以用一元一次方程式來解決有關。

中國─《九章算術》
    《九章算術》成書於漢代，集之前數學知識之大成，是中國最重要的一本算書；劉徽為其作注時，全面的證明其中的公式與解法(註一)，不但對中國後世的數學發展，甚至鄰近地區的數學發展都有深遠的影響。 
   《九章算術》第八章《方程》中共有十八個問題，都是關於一次聯立方程的問題，其中二元的問題有八個，三元的問題有六個，四元的問題有二個，五元的問題有一個，屬於不定方程(六個未知數五個方程)的有一個(註二)。屬於二元的是第二、四、五、六、七、九、十、十一問，其中第二問是：

今有上禾七秉，損實一斗，異之下禾二秉，而實一十斗；下禾八秉，益實一斗，
與上禾二秉，而實一十斗；問上、下禾一秉個幾何？
答曰：上禾一秉實一斗五十二分斗之一十八，下禾一秉實五十二分斗之四十一
術曰：如方程。損之曰益，益之曰損。損實一斗者，其實過一十斗也。益實一斗
者，其實不滿一十斗也。

術曰就是解法。〝如方程〞便是列出方程式，用現今之符號(上禾一秉x斗，下禾一秉y斗)列出：

(7x-1)+2y=10
2x+(8y+1)=10

〝損之曰益，益之曰損。損實一斗者，其實過一十斗也。益實一斗者，其實不滿一十斗也。〞就是指常數項的移項，原方程式變成： 7x+2y=11--------(1)
2x+8y=9---------(2) 至於接下來的算法便是利用方程術，由於方程術是在第一問(三元一次)後所提出的，所以第二問中就沒有再寫出計算過程，下面是我用現在的符號改寫方程術的計算過程：

(2)乘以(1)的x項係數7，得14x+56y=63--------(3)
用(3)去減(1)，直到(3)之x項係數為0，得52y=41--------(4)
(1)乘以(4)的y項係數52後，再一直減去(4)，到y項係數為0止，得364x=490，再除以原x項之係數7(即(1) x項之係數)，得52x=70--------(5)
由(4)、(5)可知上禾一秉實一斗五十二分斗之一十八，下禾一秉實五十二分斗之四十
一。

其實方程術相當於利用係數列出一增廣矩陣後再做運算，也就是將上述的過程寫成：

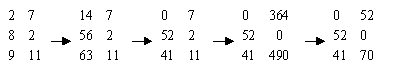
由於這只是二元的問題，並不能全盤看出方程術的法則，有興趣的讀者不妨看郭書春所著《古代世界數學泰斗─劉徽》書中第42頁，在那清楚的演示用方程術解第一問。

  《方程》章在第二問已經有了常數項的移項；第四問中不但有常數項的移項，還有未知數項的移項；而第六問中更出現了負數的情形，熟知負數發展歷史的讀者必定會明瞭此為一重大之突破；到了第十問更是出現分數係數的情形，而其解法與我們現今相同，將其化成整係數方程式後再求解。

    方程術是《九章算術》最高的數學成就(註三)，劉徽亦在此基礎上創立了方程新術，使中國數學成為這一領域中的佼佼者。

  《九章算術》在第七章《盈不足》中雖然不是用方程式的方式來解，但許多問題亦可劃歸於二元一次方程式的範疇，若能適當的引入課堂之中，必能啟發學生更多的興趣與共鳴。

    典型的盈不足問題是共買物問題：各人所出A，盈a；所出B，不足b，求人數、物價(註四)。《九章算術》給出了一般公式：

每人應出的錢=(Ab+aB)/(a+b)
物價=(Ab+aB)/(A-B)
人數=(a+b)/(A-B)

《九章算術》還給出了兩盈(或兩不足)的公式，並利用這兩組公式解決了大量的一般二元一次的算術問題(含分配問題、混合分配問題等等)，因為在這類問題中，任意代入兩個數，必定是上述兩種情形之一。舉第十三問為例：

今有醇酒一斗，直錢五十；行酒一斗，直錢一十。今將錢三十，得酒二斗。問醇
酒、行酒各得幾何？
答曰：醇酒二升半，行酒一斗七升半。
術曰：假令醇酒五升，行酒一斗五升，有餘一十。令之醇酒二升，行酒一斗八
升，不足二。

解法意思是若買醇酒五升，行酒一斗五升，則(較三十錢)盈十錢；若買醇酒二升，行酒一斗八升，則(較三十錢)不足二錢。所以就可以利用先前的公式得：

醇酒升數＝(5*2+10*2)/(10+2)=2.5升
行酒升數＝(15*2+10?18)/(10+2)
          ＝17.5升

這樣的算法既直接又快速，反觀若用現在中學所教的二元一次聯立方程式來解，就解法上而言就顯得笨拙許多。至此，不禁讓我想到埃及人在解一元一次方程式時，亦是先任意假設一數再
行運算，兩相比較之下，頗有異曲同工之妙！

巴比倫
    巴比倫人在解決二元及三元問題時有兩種方法(註五)，第一種很類似於我們現在的代入消去法；第二種今日稱為丟番圖法(Diophantine)，但這並不是丟番圖(Diophantus,約A.D.250)所創，而是他學習了巴比倫人的方法，這種方法特別適合於解決有一個方程式為x+y=s(s為已知)，此時令x=s/2+w，y=s/2-w，代入另一個方程式中便可解出w，如便可以求得x與y了。下面舉的例子是出自於漢摩拉比王朝時代(B.C.1792~1750)的一塊泥板上，雖然是二元二次的題目，但可以看出此方法的運用：

有一長方形，將其面積加上長，減去寬得183；長、寬之和為27，求長、寬及面積。
解：
假設長為x，寬為y，依題意列式，
xy+x-y=183--------(1)
x+y=27--------(2)
令y`=y-2?y=y`+2，代入(1)及(2)得 
xy`=210--------(3)
x+y`=29--------(4)
由(4)，令x=29/2+w，y`=29/2-w代入(3)，得w=1/2，
故x=29/2+1/2=15，y=y`-2=29/2-1/2-2=12

在泥板上並未出現類似未知數列式的符號算式，只有敘述計算的過程，而且是六十進位制的，有興趣的讀者可參看梁宗巨著的《數學歷史典故》。讀者不難發現，丟番圖法運用時需要較高的技巧，也就是要先把其中一個方程式化成x+y=s的形式才可，不過不論是丟番圖法或是第一種方法，在推廣到多元一次聯立方程式的問題時就顯得十分繁雜，不如《九章算術》方程術來的簡便，但巴比倫人的方法在解決非線性的問題時便可以看出其優越性，由此可以反映出巴比倫人的泥板上有許多的非線性問題，而《九章算術》幾乎沒有非線性問題的情形。

印度
    印度人在二元一次方程式方面的成就當首推阿揚巴哈一世(Aryabhata I,A.D.476~?)，他在所寫的《Aryabhatiya》中不但清楚的描述出當時印度數學的現況，更給了印度數學繼續發展的動力(註六)，關於二元一次方程式方面的成就也記載於此書中。阿揚巴哈一世他首先給出不定方程式ax+by=c的所有整數解，其方法經傳人改進後十分類似於現今的方法(註七)，概說如下：

不妨只考慮a，b互質的情形，則存在兩整數p、q使得
ap+bq=1
ax+by=c(ap+bq)
(x-cp)/b=(cq-y)/a，令之等於t，t為整數
x= cp+bt，y=cq-at

丟番圖也曾經討論過二元一次不定方程式的情形，不過他都只給出一組正的有理數解。至於在中國，清朝李銳的〝求強弱術〞雖只用以求49x+17y=A的所有整數解，但其算則(algorithm)具有一般性，也就是說可以推廣到求ax+by=c的所有整數解(註八)。
註解：
註一：參看郭書春，《古代世界數學泰斗─劉徽》
註二：參看李儼、杜石然，《中國古代數學簡史》
註三：參看郭書春，《古代世界數學泰斗─劉徽》
註四：參看郭書春，《古代世界數學泰斗─劉徽》
註五：參看George Gheverghese Joseph，《The Crest of the Peacock─Non-European Roots of Matjematics》
註六：參看George Gheverghese Joseph，《The Crest of the Peacock─Non-European Roots of Matjematics》
註七：Morries Kline著，林炎全、洪萬生、楊康景松譯，《數學史─數學思想的發展》
註八：參看洪萬生，《談天三友焦循、汪萊和李銳─清代經學與算學關係試論》
參考資料：
1. 李儼、杜石然，《中國古代數學簡史》
2. 洪萬生，《談天三友焦循、汪萊和李銳─清代經學與算學關係試論》
3. 郭書春，《古代世界數學泰斗─劉徽》
4. 梁宗巨，《數學歷史典故》
5. 錢寶琮，《九章算經點校》
6. Morries Kline著，林炎全、洪萬生、楊康景松譯，《數學史─數學思想的發展》
7. George Gheverghese Joseph，《The Crest of the Peacock─Non-European Roots of
         Matjematics》