 是西元前1700年左右的文物。下圖是原始的楔型泥板,另一圖則是對照於現代所使用之數學符號。
是西元前1700年左右的文物。下圖是原始的楔型泥板,另一圖則是對照於現代所使用之數學符號。1995年5月任教於普林斯頓大學的英國數學家安德魯˙威爾斯(Andrew Wiles)在《數學年刊》(Annals of Mathematics)上發表論文,徹底解決了歷經三百年,困惑無數數學家的<費馬最後定理>--- xn + yn = zn , 當n大於2時沒有整數解。這是當代數學界一件振奮人心的大事。關於費馬的最後定理如何被證明,坊間已有數本譯作。由於這個定理起源於眾所周知的畢式定理:對於任一直角三角形,兩股的平方和等於斜邊的平方。意即當x、y為一直角三角形的兩股,z為斜邊時,此三者滿足x2 + y2 = z2。因此,本文意圖對畢氏定理作歷史性的回顧,除了介紹神秘的畢達哥拉斯學派以外,並探討畢氏定理的意義以及此定理在數學發展歷史中所扮演的角色,希望藉由檢視的過程,對這個定理給予適當的定位。
一、畢達哥拉斯學派畢達哥拉斯學派之所以圍上一層神秘的面紗,主要是因為畢達哥拉斯嚴格要求門徒必須遵守派規,不得對外洩漏秘密所致。關於畢達哥拉斯我們所知甚少,相傳其誕生於西元前580年前後的薩摩斯島(Samos)。畢達哥拉斯曾師事愛奧尼亞學派的領導人泰利斯(Thales),離開退利斯之後,他到各地遊歷,其中包括了埃及、巴比倫等地。一般咸認為畢達哥拉斯在遊歷中汲取了相當多當時所使用之數學知識。大約於西元前540年,畢氏定居於克羅頓(Croton),並在此地創設了一所學校。此學校的成員就是今日我們所稱的畢達哥拉斯學派。
畢氏學派的宗旨是「萬物皆數」(
All is number),他們認為數是實體的最根本,所有的東西都含有數的成分,數是形成宇宙的要素。三角形數、方形數、長方形數、完美數(一個數等於比其小之所有正因數之和)等都是此學派所鍾愛的。對畢氏學派而言,所謂數僅指整數,兩個整數之比並非分數,而是另一類的數。因此當某些比值(例如等腰直角三角形一股與斜邊之比值)無法用整數之比表示時,此學派感到困惑和前所未有的疑慮。畢氏學派所選擇的處理方式是迴避,他們並不接受這種不可公度量比的數(incommensurable ratios)。除了數學之外,數與自然的關係也引起畢達哥拉斯的興趣。他認為自然現象是由規律所支配,而這些規律可以以數學方程式來描述。畢達哥拉斯經由單弦性質的研究,把關於樂聲比例的新理論應用於豎琴。單單撥弦會產生一個標準音,其是由振動著弦的整個長度產生。將弦在其長度的某處固定,會產生不同的振動和不同的音。若在弦長一半處固定弦,再撥弦後會產生一個與原來的音和諧的高八度音。同樣的在弦長的
1/3,1/4或1/5處固定弦,會產生其他的和音。但如果在整條弦長度的非簡分數處固定弦,則產生的音並不會與上述之音和諧。這是當時一個重大的發現,而這項成果也影響了文藝復興時期對音樂工作的研究。從音樂的和聲、行星運行、牛頓的萬有引力理論,在在都顯示了物理世界存在著一個數學結構。時至今日,藉由數位電腦、數位手錶、數位收音機、數位錄放影像,或者我們可以說現在已經越來越接近畢達哥拉斯所謂「萬物皆數」的世界了。畢氏學派是一個宗教的、科學的、哲學的組織,無可避免地,他們也涉入了政治活動。由於此學派附和於貴族的政治派系而受到另一黨派的追殺。雖然畢達哥拉斯逃亡到
Metapontum,還是不幸的在那裡被謀殺(約為西元前497年)。畢達哥拉斯死後,其學派的成員仍散居希臘各處繼續傳佈其學說。之後的柏拉圖、亞里斯多得、歐幾里得都傳承自畢氏學派,是希臘哲學、數學的一代宗師,此乃是後話了。二、畢氏定理的意義
畢氏定理的影響及一般化可應用到相當廣泛的領域,稱其為數學上最重要之基本定理並不為過。天文學家克卜勒(Kepler)認為畢氏定理為幾何學上的黃金,其在幾何學中所佔之份量可見一般。算術和幾何原本是不相關的領域,算術肇基於記數,是一個典型的離散過程。當計算過程結束時,算術的事實可以很清楚的被瞭解。而人們也不會期望從數值本身得到什麼意義。但幾何則不同,幾何處理線段、曲線、面等等問題,它們是連續而不是離散的物件。人們較希望看到的是幾何的事實而不是藉由計算獲致的結果。畢氏定理在這裡對於算術和幾何兩者之間所隱藏的深層關係,給予了第一個暗示,而且在數學史的發展上其在上述二領域之間處於關鍵性的地位歷久而不衰。關於畢氏定理,讀者可以很容易的發現,它對於像32+42=52這樣一個純算術的事實,存在於其中一個幾何的解釋。
一些學者認為畢氏定理在畢氏前一千年就為人所熟知。現在收藏於哥倫比亞大學的巴比倫楔形泥版322(Plimpton 322), 是西元前1700年左右的文物。下圖是原始的楔型泥板,另一圖則是對照於現代所使用之數學符號。
是西元前1700年左右的文物。下圖是原始的楔型泥板,另一圖則是對照於現代所使用之數學符號。
經過Neugebauer等學者的解釋,這份泥版是一份數學作品而且也蘊含一個合理的數學解釋。我們可以看到其上有十五組畢氏三元組。所謂的畢氏三元組就是直角三角形兩股長為a,b,斜邊長為c。若a,b,c三者無共同因素,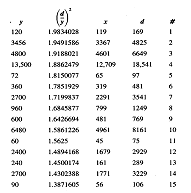
則a=(p2-q2),b=2pq,c=p2+q2。其中p,q為整數。我們可以很容易就得到,若(a,b,c) 三者互質且為一畢氏三元組,則 a和b兩者必定一為奇數一為偶數。
在數學發展的歷史中,我們常可發現數學家在不同的時空下,各自獨立地發展出相同的定理。西元前500~200年間的印度Sulvasutras也提及畢氏定理並出現了(5,12,13)(8,15,17)(7,24,25)(12,35,37)等畢氏三元組。在中國的數學史上,我們稱此定理為商高定理。這是因為於周髀算經中曾記載了這樣一段話:「昔者周公問於商高曰:『竊聞於大夫善數也,請問古者包犧立周天歷度,夫天不可階而升,地不可得尺寸而度,請問數安從出?』。商高曰:『數之法出于圓方,圓出于方,方出于矩,矩出于九九八十一。故折矩,以為勾廣三,股修四,經隅五。』」這是中國第一次出現的畢氏三元組(3,4,5)。至於勾股弦關係的一般式,則同樣記載於此算經。「陳子曰:『若求邪至日者,以日下為勾,日高為股,勾股各自乘,并而開方除之,得邪至日,……』」。
有關於此定理更詳細的敘述是在中國的《九章算術》第九章。這本算經的編纂年代大約是在東漢初期,書中收集了兩百四十六個應用問題的解法,分別隸屬於方田、粟米、衰分、少廣、商功、均輸、盈不足、方程、句股九章。九章算術之成書是因為春秋、戰國時期社會生產力逐漸提高,促進了數學的發展。當時各國的統治階級要按畝收稅,必須有測量土地、計算面積的方法;要儲備糧食,必須有計算倉庫容積的方法;要修建灌溉渠道、治河堤防和其他土木工事,必須能計算工程人工;要修訂一個適合農業生產的曆法,必須能利用有關的天文數據。那時的百姓掌握了相當豐富的、由日常生活中產生的數學知識和計算技能,《九章》之成書就是這些知識的彙整。句股章全章對畢氏定理有深入的探討。以下我們將做個簡單的介紹。
要談論《九章算術》就不能不提及劉徽,如果我們視《九章算術》為一數學骨架,那劉徽的註解就是賦予其血肉,真正地體現了《九章算術》的精神,使之成為中國古代數學的代表。相傳劉徽是三國魏晉時人,為一位布衣數學家。劉徽認為數學現象是多樣性的統一,各種各樣的數學方法都有共同的本源。他在《九章算術注原序》中寫道:
事類相推,各有攸歸,故枝條雖分而同本幹者,知發其一端而已。
劉徽注貫穿了這種認識,特別注重對數學理論追本溯源,提綱挈領,竭力引進數學中最基本的概念原理,在這個基礎上建立他的理論大廈。在數學的方法論上,劉徽主張把生動的直觀與抽象的邏輯論證結合起來。正如《九章算術注原序》云:
又所析理以辭,解體用圖,庶亦約而能周,通而不黷,覽之者思過半矣。
辭和圖不僅展現劉徽的數學成就,也顯示出劉徽高超的邏輯思想。劉徽全面證明了《九章算術》的公式解法,彌補其不足,奠定了中國數學的理論基礎。
《九章算術》的勾股章是流傳迄今的中國古代最早有系統的勾股理論。全章二十四問,大體分為兩部分:前者為以勾股定理為中心的解勾股形算法,後者屬於勾股測量問題。前後問題性質不同,解題方法亦大相逕庭。劉徽利用出入相補原理證明解勾股形的公式:
勾自乘為朱方,股自乘為青方,令出入相補,各從其類,因就其餘不移動也,合成弦方之冪。
劉徽的《九章袿蘆悛`》闡明了從出入相補到勾股比率論的理論發展過程,概括出古代勾股算法完整而嚴謹的理論體系。
尾聲如前所述,雖然各民族都出現了同樣的定理,但為何最後人們卻以畢達哥拉斯定理(
Pythagorean theorem)命名呢?這就與各民族性有關了。有些民族較重視數學之實用性,他們在意的是如何使用數學,使其對日常生活有所幫助。而希臘人醉心於心智的鍛鍊,熱衷於演繹推理,他們能純粹地欣賞數學之美,也願意致力去發掘數學本身所蘊藏之意義。所以最後對此定理希臘人真正提出幾何證明。歐幾里得的《幾何原本》收錄了相當多有關畢氏學派的數學成就,其中畢氏定理的證明編寫於第一冊命題47。至今為止,有數百種關於畢氏定理的證法。這個在古文明時代就為人所知的古老定理,時至今日仍歷久彌新。文章即將結束,經過了這些介紹,下次,當您於解題過程中運用到畢氏定理時,或許會有另一番不同的體會吧! 參考文獻Courant, Richard and Herbert Robbins,(Revised
by Ian Stewart) 1996. What is Mathematics?--2nd
ed. , Oxford
University Press, Inc.
Grattan-Guinnes, Ivor 1997. The Fontana History of the Mathematics Sciences, Fontana Press.
Heath, T. L. 1980. Mathematics in Aristotle, Garlano Publishing, Ine.
Hirschy, Harriet D. 1989." The Pythagorean Theorem(National Council of Teachers of Mathematics)",
in: Historical Topics For The Mathematics Classroom, pp.215~218.
Katz, Victor J. 1993. A History of Mathematics, HarperCollins College Publishers .
Stillwell, John 1989. Mathematics and Its History, Springer-Verlag New York Inc .
Trimble, Harold C. 1989."Number Beliefs of The Pythagoreans (National Council of Teachers of Mathematics)",
in: Historical Topics For The Mathematics Classroom, pp.51~52.
Kline, Morris 1983. 《數學史- 數學思想的發展 上冊- 數學思想的發展 上冊》(Mathematical
Thought from Ancient to Modern Time),
林炎全、洪萬生、楊康景松 譯,台北:九章出版社。
Singh, Simon 1998.《費瑪最後定理》(Fremat's Last Theorem),薛密 譯,台北:臺灣商務印書館。
D. Aczel, Amir 1998.《費馬最後定理》(Fremat's Last Theorem),林瑞雲譯,台北:時報文化。
錢寶琮《九章算經點校》,台北:九章出版社,1984。
李繼閔《九章算術〉及其劉徽注研究》,台北:九章出版社,1992。
郭書春《古代世界數學泰斗─劉徽》,台北:九章出版社,1995。