
「算學何為乎學,難題易題,盡無不明之術也。雖說理高尚,解術迂闊者,乃算學之異端也。」關孝和
關孝和小傳
西元1642年,關孝和出生於上野國藤岡的一個武士家庭。他是四代將軍德川家綱的家臣,領有三百石的俸祿。關孝和從小就展露其計算上的才能,在六歲時,由於指出大人布算的失誤,眾人皆稱其為神童。剛開始,他授業於高原吉種,長大後,其傑出的才能日益發揮,天文律曆莫不精通,出類拔萃於同儕之上。關孝和發現了很多新的定理,他的成果彙集成數百卷,日本人尊為算聖。
關孝和在世,對門下弟子教授珠算法、算籌法、演段法、及點竄術,隨著這些課業的熟習,會頒與五階段的證書。他終生無子嗣,收養姪子新七為養子,後於1708年病逝,葬於淨輪寺,享年67歲。由於新七品行不端,終至招罪於幕府而被抄家。此後嗣絕孫亡,關孝和墓地凋零荒廢。到了1794年,齋藤正順等人路過此寺,偶然間發現殘破的墓碑,撥開滿佈的蘚苔後,才發現是關孝和的墳墓,所以聚集了8人合資建碑,使廢塚得以復原,此乃後話了。關孝和對和算貢獻非常大,可說是日本學問之代表。在數學方面其有獨特的見解,並且對日本及中國的數學文獻不但涉獵極深,也加以系統的整理分析。因此,日本數學史家小倉金之助讚譽關孝和是個集「獨創家」和「組織家」於一身的天才『關孝和は實に、獨創家であると同時に、組織家をも兼ね合せた天才であつたのでした』(小倉金之助,1941)。
17世紀的日本關流代數
17世紀後期日本的數學史上值得一提的就是類似法國Viete所創的代數學派,其創辦人正是關孝和。這門數學藝術是關孝和沿革中國的代數天元術而來,何謂天元術呢﹖通常用求解方程的方法來解決實際問題,首先要設未知數,再按著問題所給的條件,列出一個包含所設未知數的方程,再接著是解方程,求出未知數。西元十一至十三世紀的中國古算家,不僅創造了增程開方法,用來求解高次方程的普遍解法,也創造了根據已知條件可以列出方程的方法,這就是天元術。天元指的就是問題中的未知數,「立天元為某某」即為「設x為某某」的意思。用天元術來記多項式或方程,常常是在一次項旁記一個“元”字,或再常數項旁記一“太”字。中國古算書中有關天元術的著作流傳至今日者只有李冶的《測圓海鏡》、《益古演段》、朱世傑的《算學啟蒙》以及《四元玉鑑》。
究竟關孝和如何得知天元術並加以改革?天元術是經由元朝朱世傑《算學啟蒙》的重印本傳入日本。《算學啟蒙》成書於1299年,而久田玄哲於1658年重新出版。《算學啟蒙》一書全面地介紹了中國宋元數學-包括了天元術在內的一切內容,對日本數學的發展產生了比較大的影響(李儼,1983),而在那時候天元術在中國幾乎已被遺忘。至於其被遺忘之原因,我們會於後面的篇幅再加以討論。在1671年澤口一之出版《古今算法記》,這本書是目前所知第一本正確了解和操作天元術的日文書籍。而更重要的一件事是,澤口一之在書末留下了15題未解的數學問題,因為其無法利用天元術的方法求解。所謂的遺題承繼是日本和算的特色,某和算家在自己所著的和算書卷末,提出一些數學難題以示讀者。其弟子、門人、或其他讀者在經過努力研究,解決了難題之後,一般要著難題解答之書,並在卷末更加深入的揭示問題,提出難度更高的問題,讓有心人士去研究解決,從而進一步更深入的研究。關孝和在他於1675年年初出版的標題為《發微算法》的小書中試著解決了所有的問題,這本小冊子是關孝和有生之年唯一出版的一本著作,但只是簡單的表示澤口一之的問題及解答,並沒有列出詳細的解題過程。因為在中國數學的傳統中,此種解題形式是相當常見的。
後來關孝和最有天份的傳人建部賢弘(1664-1739)在1685年出版了《發微算法演段諺解》,
為這本書提供了詳細的註解。也就是建部賢弘的註解,使得關孝和的改良代數第一次廣為人知。關孝和的改良代數首先稱之為傍書法,後來松永良弼又改稱為點竄術(意即以符號表示和消去的技術)。關孝和改良中國的天元術,用文字符號表示未知數。並推廣此種方法至數個未知數的過程,而形成了一個代數的新系統。由有甚之,關孝和的代數是一個用書寫形式的計算方式。這也就是為何有人把關流代數類比為Viete的原因。下圖即為一例。
因此,從17世紀末以後,日本的數學家能夠處理類似a-bx+cx2-dx3=0以及
3y3+5xy2-8x2y+4x3=0等代數方程式。(像這類把符號代數應用至解數個未知量在早期只出現於西歐及日本,但是在歐洲的符號代數是以古典希臘數學以及中世紀阿拉伯數學為始祖,另一方面,在日本的符號代數卻是研襲於中世紀中國的操作型代數。
朱世傑之《算學啟蒙》
如前所述,談到關孝和,就不得不提及於宋元間與秦九韶、李治鼎足而三的朱世傑。他的著作《算學啟蒙》共分上、中、下三卷,凡二十門,二百五十九問。書中涉及了四則運算、開方、天元術以及垛積等多方面的數學內容。該書涉獵之課題相當廣泛,並且由淺入深,包羅無遺,形成了一個完整的體系,既為實際應用提供了工具,也為深造闢了蹊徑,是一部很好的啟蒙讀物。因此祖頤稱《算學啟蒙》與《四元玉鑑》相為表裏,『此書首列乘除布算諸例,始於超徑等接之術,終於天元。如積開方,由淺近以至通變,循序而進,其理易見。名曰啟蒙,實則為玉鑑立術之根。』在《算學啟蒙》卷下第五開方釋鎖門中,朱世傑系統的講解了利用天元術來解決各種問題的算法。可惜的是,宋元時期中國數學許多重要的發展並沒有持久,反而迅速衰落。到了西元十五世紀,明朝的一些數學家,對天元術、四元術就幾乎全然無法理解。在整個明朝以至清初數百年間,這些學問幾成了絕學。
導致此種現象的原因很多,其中相當主要的就是這種發展脫離了當時的社會需要。以天元術為例,當時應用在生產實踐上的實很少見。考察當時社會經濟需求,需要求解四次或四次以上的高次方程問題,在當時都不是從生活和生產實際中產生出來的。脫離了社會的需要,其內容又都艱深不易了解,構成了這些成果失傳的主要原因。而且當時明朝有關商業貿易的發展大增,對數學提出了日益繁複的計算任務。有大量大部分為加減乘除的計算問題需要計算的更快和更加便利。在此種狀況下,籌算已不敷使用,因此一種新的計算工具-算盤由焉產生。也由於如此,《算學啟蒙》成書之後四百餘年,它在國內的流傳情況尚不清楚,明朝的《永樂大典》也未收集此書。但它流傳到朝鮮、日本後,產生了巨大的影響。在朝鮮李朝,它是教材和選拔算官的基本書籍之一,其算學的考試科目就明訂有「啟蒙算」(金容雲等,1978)。世宗本人還曾於1430年向當時副提學鄭麟趾學習此書。《算學啟蒙》在朝鮮已知的刻本有1433年慶州府刻本以及1660年金始振刻本。《算學啟蒙》在中國曾一度失傳,後來羅士琳讓人從北京琉璃廠書肆中訪獲金始振重刻本,詳加校勘,於1839年在楊州刊行,這本書才又重行問世。
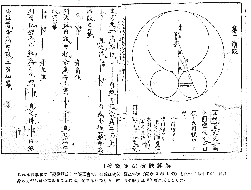
天元術與點竄術之比較綜而言之,天元術與點竄術之不同,可分為下述兩點:其一為利用天元術解任何高次方程式僅知求一正根(錢寶琮,1932),但點竄術在解二次式時就已知有兩根。例如在關流算法七部書之病題明致中的變題定究第三中,有如下的例題:假如有半梯。外斜一尺六寸,內斜一尺九寸。只云左右闊和一尺八寸。問右闊。其答案為:初。右闊七寸。左闊一尺一寸。後。右闊五寸。左闊一尺三寸。其二為天元術以算木運算,稱為器具代數(小倉金之助,1941)。而點竄術則是用傍書筆算法。因為是採用筆算法,所以在解法上,我們就可以在一個以文字表示的未知數後,再設補助未知數。然後列出聯立方程式,再依其關係逐一消去,最後成為一個一元方程式。由於成為一元方程式,就可適用於天元術,解出答案。而天元術僅能設一未知數,由於受到籌算記法的局限性,就算是之後的四元術,也只能解不高出四元以上的問題(李儼,1983)。因此點竄術是較有彈性的。下圖取自關孝和發微算法的解釋書《發微算法演段諺解》,以《古今算法記》的遺題為例。另一圖為其說明。
在點竄術之外,關孝和還有一系列包含近世數學萌芽的成果,主要的有圓理、行列式概念、垛積、極值條件等等,除了關孝和本身,他的門人中也是人才輩出,再加上其他流派的努力,共同創造出了日本數學的黃金時代。

參考文獻:
李儼(1983).《中國古代數學簡史》,台北:九章出版社。
劉鈍(1997).《大哉言數》,遼寧:遼寧教育出版社。
那日蘇(1992).〈日本和算中的遺題承繼與算額奉揭〉,《數學史研究文集第三輯》,內蒙古大學出版社,
台北:九章出版社。
洪萬生 (1996).〈數學史與代數學習〉,《科學月刊》第二十七卷第七期,pp.560~567。
李文林主編(1998).《數學珍寶-歷史文獻精選》,北平:科學出版社。
東京數學物理學會 (1907).《關流算法七部書》,東京:東京帝國大學理科大學。
大矢真一、片野善一郎(1979).《數字と數學記號の歷史》東京:裳華房。
日本學士院編(1983).《明治前 日本數學史》,東京:岩波書店。
金容雲、金容局(1978).《韓國數學史》,東京:槙書店。
錢寶琮(1932).《中國算學史》,北平:國立中央研究院歷史語言研究所。
遠藤利貞遺著(1918).《日本數學史》帝國學士院藏版,東京:岩波書店。
小倉金之助(1941).《日本の數學》,東京:岩波新書。
Sasaki, Chikara(1999).“The
French and Japanese Schools of Algebra in the Seventeenth Century:A
Comparative
Study”,Historia Scientiarum
Vol.9-1(1999),The History of Science Society of Japan.