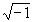是方程式x2+1=0的根，在合理的推論之下，虛數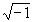應該是誕生在二次方程中。如果你也這樣以為，那麼數學史家的觀點，絕對出乎你的意料之外。在數學史的發展過程中，早期的數學家面對方程式x2+1=0時，和我們現在的國中數學課本處理方式一樣，他們認為這樣的方程式是無解，當然也就沒有發明一個數來表示方程式x2+1=0的根。因此，當我們回顧虛數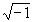誕生的故事時，便會認同數學史家的觀點，虛數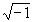並非誕生在二次方程式中，而是在三次方程。
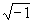的誕生
台師大數學系碩士班研究生
陳鳳珠
一般人都知道虛數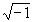是方程式x2+1=0的根，在合理的推論之下，虛數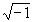應該是誕生在二次方程中。如果你也這樣以為，那麼數學史家的觀點，絕對出乎你的意料之外。在數學史的發展過程中，早期的數學家面對方程式x2+1=0時，和我們現在的國中數學課本處理方式一樣，他們認為這樣的方程式是無解，當然也就沒有發明一個數來表示方程式x2+1=0的根。因此，當我們回顧虛數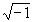誕生的故事時，便會認同數學史家的觀點，虛數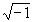並非誕生在二次方程式中，而是在三次方程。
關於虛數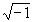誕生的故事，可以從西元1545年義大利的學者卡當諾（G.
Cardano，1501-1576）談起。卡當諾是數學史上有名的怪人，不但博學多才，通曉醫學、數學與天文學，且喜好賭博與占星術。他對當時的一切知識相當投入，著述豐富且涉及許多方面。在1545年時，卡當諾發表了他的傑作《大術》（Ars
Magna，原意為「偉大的技藝」），其中介紹一般三、四次方程的求根公式最為著名。書中首先以具體方程為例，說明了（不完全）三次方程x3+mx=n
（m、n為正整數）的解法：「將x項係數的三分之一自乘三次，再加上方程式常數項係數n一半的平方，將兩者之和開平方。將此過程重複一次，其中一根加上常數項係數n的一半，另一根則減去常數項係數n的一半……然後前者的立方根減去後者的立方根，剩下的即為x的值。」換言之，所謂卡當諾公式解即是
x =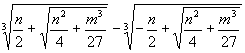 
。
例如卡當諾求解三次方程x3+6x=20時，根據他的公式可得到
x=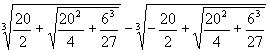 
=
。
卡當諾的論證純粹為幾何性質，涉及單純的立方體與其體積。用現代的代數方法說明，亦即設t-u=x，則原方程式x3+mx=n變成（t-u）3+m（t-u）=n，
利用立方和公式展開
t3-u3-3tu（t-u）+m（t-u）=n，化簡後得t3-u3+（t-u）[m-3tu]=n。觀察後，令
3tu=m與t3-u3=n，從前式可得u=m/3t，然後帶入後式得到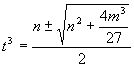
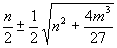，兩邊再乘以t3，且重新整理可得方程式
。若將此方程式視為t3的二次方程式：
，利用早已為當時數學家所熟知的二次方程式公式解得出：
=
=
，
接著將
t開立方可得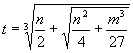
。我們從u3=t3-n，便知
或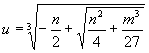
。
最後，我們得出三次方程式
x3+mx=n的卡當諾公式解x = t-u=。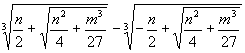
要特別注意的是，十六世紀時的數學家要求方程式中的係數必須為正數，因此，卡當諾在書中分別針對x3=mx+n、x3+n=mx等等（不完全）三次方程，提出了以現代眼光來看似乎是多此一舉的公式解。《大術》的最後，卡當諾做出了結論，他認為三次方程已獲得解答。事實果真是如此嗎？答案顯然是否定的，因為他所處理的是不完全的三次方程，並非針對一般的三次方程式。儘管如此，對於三次方程的解決，卡當諾公式仍令人感到相當振奮。不過，卻也因為卡當諾公式的出現，引出了一個數學史上的重要難題。
接著出現的難題，卻成為虛數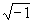誕生的契機。當我們考慮到三次方程x3=15x+4時，卻出現了令當時數學家難以解釋的結果，因為根據卡當諾的公式解可得x=
。就當時數學家的觀點，出現負數的平方根絕對是不合理的，所以很容易忽略它，而認為這個三次方程是不可解。然而，我們卻可以輕易的檢驗出x=4是此三次方程的一個解，但是為何在利用卡當諾公式所求得的結果中，卻沒有看到x=4出現？究竟所得到的解
和4有沒有關係呢？
事實上，卡當諾早已遇到虛數根的問題。他在《大術》第三十七章中，提出並解決這樣的問題：「把10分為兩部分，其中一部份乘以另一部份結果為40…因此，將分成的兩部分應是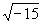5+
和5-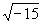。」並且分析：「讓我們解除思想的束縛，用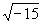5+乘5-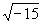，我們便得到25-（-15），也就是25+15。因此乘積為40。」然後，他寫道：「算術就是這樣的精巧奇妙，它最根本的特點，正如我所說過的，是既精妙又無用。」雖然卡當諾已經遇到虛數根，但卻未能解決三次方程所謂“不可約”（即判別式為負）的情形。關於卡當諾所面對虛數根的困惑，數十年後另一個義大利數學家邦貝力（R.
Bombelli，1526-1573）提出了他的深刻想法。
邦貝力認真看待虛數，用它解出不可約三次方程，並建立了虛數的運算法則，這是人們對數認識的一大進步，儘管他仍認為虛數是人為而非真實的數。針對三次方程x3=15x+4的兩個解和4的關係，他暫時拋開當時數學家對虛數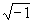
潛在的成見，提出了不受侷限的奇妙想法。因為 
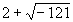和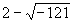 
只是運算符號上的差異，所以他大膽地令
=
和
= 
，將開立方的結果和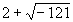作對照可得a=
2，b= 1，然後檢驗出x==（
）+（
）=
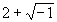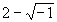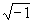4。如此，邦貝力不但賦予了虛數的意義，並且也發展出虛數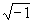的運算法則，奠定了虛數理論的基石。用現在的符號i=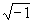（尤拉在1748年提出）表示，除了乘法運算法則：
，
，
，
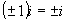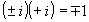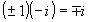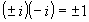，也包含虛數的加法與乘法運算，例如：
和
。邦貝力深刻洞悉了虛數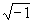在代數中所扮演的角色，不愧為十六世紀義大利的偉大數學家之一。
在虛數尚未在數學王國之中取得正統地位之前，許多數學家和卡當諾一樣，認為虛數是不存在的。在1629年，荷蘭數學家吉拉德（A.
Girard，1595-1632）曾臆測每個次數大於0的虛數係數方程式至少有一個虛數根，他為了找到方程式根與係數的關係，表示應該接受虛數，至少把它看成是方程式「形式」上的解，如此才能保證n
次方程式必有n個根。此外，笛卡爾（G. Descartes，1596-1650）把負根稱為“假根”（false
root），而將前述這種形式的根稱為“虛根”（imaginary root），這就是虛數（imaginary
number）這個名詞的來源。後來，高斯認為必須將虛數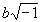
和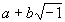
區別，才引進複數（complex
number）。笛卡兒曾說道：「方程式的根不一定是實數，有時他們可以是虛數。」他辯稱負根可由方程式的變換轉為實根，但虛數根則無法辦到，因此它是虛根而不是實根，它們並不是數目。由此可見，笛卡兒仍是無法接受虛數。甚至牛頓（I.
Newton，1643-1727）也不覺得虛數有什麼特別意義，可能是因為當時無法發現虛數的物理意義之緣故。
虛數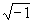的地位，一直要到兩世紀後經過尤拉（L.
Euler，1707-1783）、高斯（F. Gauss，1777-1855）和柯西（A. Cauchy，1789-1857）的努力，才算在數學王國之中取得正統。
十六、七世紀的數學家，大都把虛數看成是不可能或是不存在的，約翰•白努利（Johann
Bernoulli，1667-1748）在1702年的發現引起了相當的震撼。他把虛數引進分析學中，例如：
。然而，自從納皮爾（J.
Napier，1550-1617）發明對數以來，一直都只容許正數才有對數，約翰•白努利在上列的式子裡，卻出現了虛數的對數，因而引發了長達三十多年的爭議，亦即負數和虛數是否有對數？
關於負數是否有對數的爭論，首先由萊布尼茲（G. W. Leibniz，1646-1716）和約翰•白努利開始，從1712年到1713年之間共長達十六個月。萊布尼茲的看法是負數沒有對數，或者更正確地說，負數沒有實數值的對數。可是，約翰•白努利積極想證明負數有實數值的對數，雙方各持己見沒有定論。後來，這個爭論也發生在約翰•白努利和他的學生尤拉（L.
Euler，1707-1783）之間，約翰•白努利仍堅持十多年前的想法，
尤拉卻不同意約翰•白努利所提出的等式：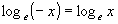
，但尤拉自己也沒有明確的想法。尤拉在1740年在寫給約翰•白努利的信中提及指數、三角函數和虛數的一個關係式，他認為y=2cosx與y=eix+e-ix是同一個微分方程式的解，因此，兩個函數應該相等。這個結果在1747年發表，亦即複變分析學中最根本的公式：
，
，
。
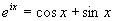直到1747年，尤拉才提出多值函數的概念來定義非零負數的對數。除了定義虛數的對數外，尤拉在1749年又利用虛數的對數，來定義虛數的虛數乘冪。後來，高斯在1799年的博士論文中，證明了代數基本定理：「每個次數大於0的虛數係數方程式至少有一個虛數根。」他在論文中說道：「只要分數、負數與實數都已完全瞭解，那麼虛數是可以容忍的。」換言之，只要實數系有嚴密的邏輯基礎，那麼虛數的邏輯基礎就沒有問題了。
高斯對虛數邏輯基礎所做的註解，引起了柯西和漢彌頓（W.
Hamilton，1805-1865）的回應。柯西採用純代數的方法來定義虛數，他仿照同餘的概念，根據對模實數係數多項式x2+1做同餘類，給出了嚴密且抽象的複數定義。柯西給的複數定義是相當抽象的，另一個較具直觀性的定義，是由漢彌頓在1837年的論文中所提出來，他把複數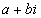
定義成有序實數對
。根據這樣的定義，只要實數系有了嚴密的邏輯基礎，複數系也就會有邏輯基礎了。
數學家之所以願意如此為虛數「扶正」身分，全都是因為它十分「有用」。
虛數發展至今，在處理代數、分析、幾何與數論的問題上，皆可看到複數的蹤跡。讓我們觀察恆等式：（22+32）（42+52）=
533 = 72+ 222 = 232+ 22和
（172+192）（132+152）=
256100 = 642+ 5022 = 82+ 5062。它們會是一種巧合嗎？事實上，它們僅是數論中定理的例子，亦即：（a2+b2）（c2+d2）=
A2+B2 = C2+D2。我們利用虛數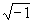便可清楚得到印證：
（a2+b2）（c2+d2）= [（a+bi）（c+di）] [（a-bi）（c-di）]
= [（ac-bd）+（ad+bc）i] [（ac-bd）-（ad+bc）i]
=（ac-bd）2+（ad+bc）2
（a2+b2）（c2+d2）= [（a+bi）（c-di）] [（a-bi）（c+di）] =（ac+bd）2+（ad-bc）2。或者讀者願意試試（892+1012）（1112+1332）= A2+B2 = C2+D2，找出其中A、B、 C和D分別是多少？
任何數學知識的發展，都是由解決問題開始，虛數的誕生當然也不例外。希臘數學家丟番圖（Diophantus，250-275）的《算術》（Arithmetica）書中，就已出現負數根的問題：「一直角三角形周長為12面積為7試求其邊長」，但是丟番圖並不考慮虛根的問題，一直到卡當諾才去面對方程式中的虛數根，雖然他認為虛數是精妙卻無用，卻引起邦貝利對虛數的興趣，進一步研究虛數的運算法則。因為方程式的虛數根是不可避免的，虛數不應輕易再被忽視，數學家也因此被強迫去面對虛數。
當然，要讓數學家就此接受虛數是不容易的。正如吉拉德雖然認為要接受虛數，但卻將它視為「形式」上的根；笛卡兒一樣也難以接受虛數，認為是它並不是數。那麼是何種理由，奠定了虛數在數學王國裡的地位呢？在經過尤拉、高斯和柯西等人的努力，除了虛數可以滿足數學家天生對完美的渴望外（例如：滿足算術基本定理），更重要的是它相當「有用」。正如吉拉德所說：「有人可以說這些不可能的解有什麼用？我回答：它有三方面的用處－一是因為它能肯定一般法則；二是它們有用；再有，還因為除此之外再沒有別的解。」總之，它的誕生與發展，倒真地呼應了克萊恩（M. Kline）所言：「虛數……其強自佔入算術計算也，不特未嘗獲得世人之承諾，抑且與算學家之始願相違，但終以日積月累之功，在其表現效能範圍之內，流行日廣。」
回顧了虛數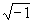誕生的過程，值得一提的是虛數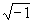的出現，與一般人所認知的並不相符。它之所以出現在數學的領域，並不是用來作為解二次方程式的工具，而是誕生在三次方程x3=
15x+ 4解法的懷抱中。這不是很出乎我們的意料之外嗎？
參考資料：
李文林主編，1998，【數學珍寶】，北京：科學出版社。
洪萬生，1991，【孔子與數學】，台北：明文出版社。
Dunham, W.，1998，【天才之旅】，台北：牛頓出版社。
Kline, M.，1983，【數學史】，台北：九章出版社。
Glas, E., 1988, ‘Fallibilism and the Use of History in Mathematics Education’. Science & Education 7：361-379.
Kleniner, I., 1988, ‘Thinking the Unthinkable: The Story of Complex Numbers（with
a Moral）’. Mathematics
Teacher. October. 583-592.
Nahin. P. J., 1998, An Imaginary Tale: The Story of .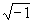
Princeton University Press.
NCTM, 1989, Historical Topics for the Mathematics Classroom. Washington, D. C.: NCTM.