∼ 給我一個立足點,我就可以移動這個地球。∼
台師大數學系碩士班研究生 陳鳳珠
一、前言
阿基米德(Archimedes,287?-212 B.C.)是古希臘的偉大數學家,經歷了二十二個世紀,他在各方面的貢獻至今仍受到許多的尊崇。他擁有極高的天賦,不但與牛頓(I. Newton,1643-1727)、高斯(C. F. Gauss,1777-1855)並列為三個最偉大的數學家,也是傑出的物理、天文學家和機械發明家。
阿基米德在繼承前人數學成就的基礎上,做了進一步的完善和發展。他不但給出了阿基米德公理,完成圓面積、球表面積和球體積等公式的證明,還研究了與螺線、拋物線和圓錐曲線旋轉體有關的命題,同時在三次方程和數論方面都有貢獻。阿基米德亦是數學和物理結合研究的最佳典範,他用公理方法完成了槓桿平衡和重心的理論,而且在他的著作《論浮體》中,應用公理方法完成了流體浮力的理論,因此成為靜力學創始人。不僅如此,他還透過力學的實際應用發明了許多實用機械,也曾在《球體設計論》介紹了一種用來展示太陽、月亮和五顆行星環繞地球的設計。
由於阿基米德在各領域均有傑出的表現,因此有許多關於他的傳奇和故事。也許這些故事並非完全確實,但可以幫助我們了解這位古代最偉大的數學家的個性。其中最著名的一個故事,就是發現金鑄皇冠純度的方法。Syracus國王定製了一頂皇冠,交貨以後,他懷疑這頂皇冠的純度不足,所以請阿基米德檢驗其成分;阿基米德一直在思考這個問題,有一天當他洗澡時,觀察到自己的部分體重被水的浮力所抵消,突然間他領悟了解決這個問題的方法,他對於自己這個發現感到相當興奮,以致於竟然裸奔到街上大叫 “Eureka!(我找到它了)”。他發現物體沉入水中時,被水的浮力所抵消的重量等於排出水的重量,這正是流體靜力學第一運動定律,因而藉此解決了國王交給他的問題。由此可見,阿基米得是全神貫注所研究的問題,才會忘記穿衣服就興奮地奪門而出。
另外,一個流傳下來的阿基米德名言是:「給我一個支點,我就可以移動這個地球。」他這樣誇口是因為被自己發現的槓桿原理深深感動。故事是他對Syracus國王宣稱任一給定的重物都可以由一個給定的力移動,Syracus國王便要求他給出一小的力可以移動巨大重物的實例。因此,阿基米德設計了一種機械,把一條全體敘拉古居民共同使力也無法移動的一條船,將它變成只需一個人就可移動,進而給予他所發現的定理一個實際例證。
儘管阿基米德在物理和機械等等各方面,均有不凡的表現,其中最令我們感興趣的部分,是他在數學方面的研究。尤其是他在嚴密證明之前所呈現啟發性的論述,亦即那種利用物理觀念的推理來解決數學問題的方法。所以,本文針對阿基米德在嚴密論證前所提供「發現的方法」,介紹《方法》(The Method)中的兩個命題作為說明,1企盼大家能藉此更貼近偉大數學家阿基米德的想法。
二、發現的方法
值得注意的是,阿基米德在幾何方面的研究和歐幾里得(Euclid,約300B.C.)有很大的差異。他在嚴密綜合證明定理之前,先呈現定理「發現的方法」或是問題情境的分析,從中我們可以撥開事物的表面,洞察到他探求真理的方法。他根據力學原理所得到之「發現的方法」,研究了許多有關面積與體積方面的重要結果,而成為他最具價值的著作《方法》之主要內容。
他所提供「發現的方法」,主要是利用槓桿原理(力矩平衡),討論兩圖形之橫剖面的平衡關係。然而,他並沒有利用這種方法來演示嚴密的證明,因為我們並不能證明一個圖形是由它的各個橫剖面所組成,亦即一個平面圖形是由直線組成或一立體是由一薄平面組成。正如他自己寫道:「我常藉機械的方法來了解某些定理,但由於這些方法無法提供真正的證明,所以幾何證明是必須的。」因此,阿基米德和他同時代的希臘人一樣,堅持所有的數學結論只有通過演繹推理才能確定。他在《方法》中特別強調「發現方法」和「嚴格證明」這兩者的差異,即(1)發現定理所用的方法,雖然不能做為定理的嚴格證明,卻足以說明定理的真實性;(2)這些定理的嚴格證明,就是說這些定理最後被確認之前,必須經過無懈可擊的幾何方法論證。
儘管阿基米德認為嚴密的幾何證明是必要的,他也強調力學方法是相當有用的。如同阿基米德在《方法》的前言提及:「通過力學方法我對一些問題首先變得清晰了。然而,當我們用這種方法預先獲得有關這些問題的信息時,完成它們的證明,當然要比沒有這些信息的情形下去發現其證明容易得多。」
(一)、《方法》中的命題1
我們首先介紹阿基米德利用力學原理所呈現「發現的方法」的典型例子,亦即《方法》中的命題1:
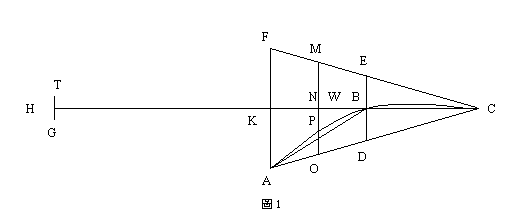
設是ABC由直線AC和拋物線ABC所為成的拋物線弓形,D為AC的中點。作直線DBE平行於拋物線的軸,連接AB、BC。則弓形ABC的面積是三角形ABC面積的4/3。(見圖1)

阿基米德的做法是先由A點作AKF平行DE。設拋物線在C點的切線分別交直線DE、AF於E、F。然後,延長CB交AF於K,再延長CK至H,使KH=CK。
因為他想證明圖形中的三角形CFA和將重心移至H點的弓形ABC,以K點為支點時呈現平衡狀態。所以,將CH作為槓桿,K為其中點。然後,設MO是任一條平行ED的直線,它與CF、CK、AC分別交於M、N、O,與曲線交P點。
現在,已知EB=BD;MO : PO=CA : AO(參看《求拋物線弓形面積》命題5)。由於線段FA、MO都平行線段ED,並且EB=BD(圓錐曲線的理論已證),2可得知FK=KA和MN=NO;又MO:PO=CA:AO與KH=CK,利用《幾何原本》Ⅵ.2得到MO:PO=CA:AO =CK:KN=HK:KN。
再取線段TG=OP,將之以H為中心放置。
由於N為MO的重心且MO:PO=HK:KN,可推知H處的TG和N處的MO,以K點為支點時保持平衡。(《論平面圖形之平衡》,Ⅰ.6.7)
類似地,對平行於DE且與拋物線弧相交的所有其他線段,即「截於FC、AC間,中點在KC上」和「曲線ABC與直線AC間的截線,H為重心放置」,以K點為支點時將保持平衡。因此,K是由如下兩組線段構成的整個系統的重心:(1)截於線段FC、AC間,置於圖中所有像MO一樣的線段和(2)中心置於H處,所有與曲線ABC間的截線如線段PO有相同長度的線段。
因為三角形ACF由所有像MO一樣的平行線段所組成;弓形ABC由所有像PO一樣含於曲線內部的線段組成。所以,可以推知,置於圖中所示位置上的三角形ACF與以H為重心放置的弓形CBA,以K點為支點時保持平衡。
最後,討論弓形ABC和三角形ABC之間的面積關係。在KC上取W點,使CK=3KW,則W是三角形ACF的重心。於是,三角形ACF : 弓形ABC=HK:KW=3:1。從而,弓形ABC=(1/3)三角形ACF,但是三角形ACF= 4三角形ABC,故弓形ABC=(4/3)三角形ABC。
阿基米德為了區別發現方法和嚴密證明的不同。於是,在證明的最後補充說明:「這裡所陳述的事實不能以上面所用的觀點作為事實證明,但這種觀點暗示了結論的正確性,鑒於該定理並未得到證明,同時它的真實性又值得懷疑,因此我們將求助於幾何學上的證明,我本人已發現並公佈了這一個證明。」(見《求拋物線弓形的面積》命題16)
我們可以發現,阿基米德在這個命題裡,除了利用到力學方法中的槓桿原理,並且將平面視為由平行的直線所組成,這樣的想法相當於後來在十七世紀發展出來的「微元」(infinitesimals)概念,亦即將平面分割成無限多條直線作「細微分割」(indivisibles)。3
(二)、《方法》中的命題11、12
接著我們再看看另一個也應用到槓桿原理及相當於「微元」技巧論證的定理。這也就是《方法》中的命題11:
如果一圓柱內接於底為正方形的直棱柱中,其中圓柱的兩底位於兩相對的正方形面上,圓柱面與其餘的四個矩形相切,通過圓柱的一底圓的圓心C與另一底圓相切的正方形的一邊作一平面X,則由該平面X所截圓柱部分圖形(簡稱:部分圓柱)的體積只是整個棱柱的1/6。(見圖2、圖3)阿基米德在命題11的一開始就說道:「這一個命題可以用力學方法加以考察,在我能夠清楚表達他之後就將用幾何角度著手其證明。」
實際上,他所利用的力學方法包含在命題11、12中。4在命題11裡,他要證明的是:以F為重心放置的部分圓柱和原位置上的半圓柱PER,以G點為支點時保持平衡。
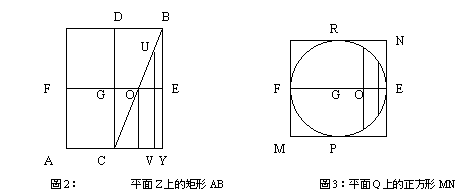
開始先假設有一直棱柱,在其內部內接一圓柱。再假設棱柱被一平面Z所截,該平面Z經過棱柱和圓柱的公共軸CD且與圓柱的底面垂直。然後,令得到直棱柱的縱截面為矩形AB,它與平面X的交線是直線BC。(見圖2)
另外,作一線段EF平分線段CD,設交於G點;通過線段EF作垂直線段CD的平面Q,令平面Q截直棱柱的橫截面為正方形MN,又截圓柱所得橫截面為圓EPFR,設G點為圓心。(見圖3)
然後,假設平面Q與平面X交於直線KL,而且線段KL與線段GE互相平分於O點。再作圓EPFR的任一條弦TS,使得弦TS與線段EF垂直且相交於I點;並且過TS作一平面W與線段EF垂直,則平面W與部分圓柱相交於一矩形,其一邊等於線段TS,另一邊平行線段UV。(見圖2和圖3)
然而,因為線段UV、BY和GC皆互相平行,而且EC為矩形,所以EG:GI=YC:CV=BY:UV=(位於半圓柱中的矩形):(位於部分圓柱中的矩形);
又EG=FG。因此,FG:GI=(位於半圓柱中的矩形):(位於部分圓柱中的矩形)。(見圖3)
假設將位於部分圓柱中的矩形移至F點,使F點為其重心;又假設線段EF為槓桿、G為其中點。由於I是位於半圓柱PER中的矩形的重心,當部分圓柱中的矩形以F為重心放置時,可推知重心為I的半圓柱PER中的矩形,與重心放置於F點的部分圓柱中的矩形,以G點為支點時保持平衡。
同理,作任一平面垂直於線段EF,並且經過半圓PER中由線段EF垂直平分的任一其他弦,截得的其他矩形截面有類似的結論。
如果考慮分別組成半圓柱和部分圓柱的所有矩形,則可得知半圓柱PER,與重心放置於F點的部分圓柱,以G點為支點時保持平衡。
接著在命題12裡,阿基米德想要證明:半圓柱PER和棱柱GHM,以G點為支點時保持平衡。(見圖4)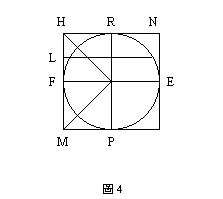
他必須先證明:分別處於原位置上的微元(1)邊等於KS的矩形和(2)邊等於LW的矩形關於S保持平衡。也就是說,要先證明處於原位置上的直線SK和LW,以S 點為支點時保持平衡。
現在,已知(圓PERF的半徑)2=SK2+SG2,即SL2=SK2+SW2。因此,得LS2-SW2=SK2,從而(LS+SW)LW=SK2,得到(1/2)(LS+SW):(1/2)SK=SK:LW。
又(1/2)(LS+SW)是LW的重心與S點的距離,而(1/2)SK是SK的重心與S點的距離。因而分別處於原位置上的線段SK和LO,以S點為支點時保持平衡。
同理,對其他相應的矩形也有類似的結論。
考慮分別位於半圓柱和菱柱中的所有矩形微元,可以發現分別處於原位置上的半圓柱PER和棱柱GHM,以G點為支點時保持平衡。
從這一結果和命題11的結論,我們可立即推出由圓柱上截得的部分圓柱的體積。因為命題11表明以F為重心放置的部分圓柱,與處於原位置上的半圓柱,以G點為支點保持平衡;根據命題12得知在半圓柱所在的位置上,可以用棱柱GHM代替半圓柱,即相對於RP將棱柱GHM往反方向旋轉。如此放置的棱柱的重心位於GE上的Z點,則滿足GZ=(2/3)GE。
若假設該棱柱置於其重心處,則(部分圓柱):(該棱柱)=(2/3)GE:FG=2:3,故(部分圓柱)=(2/3)(棱柱)=(1/6)(最初棱柱)。5
命題11和12主要是將立體的直棱柱與圓柱作「細微分割」成多個矩形平面,這裡所運用相當於「微元」的論證方式和命題1是如出一轍。阿基米德藉助線元素處理平面面積或藉助面積元素處理立體體積,這樣的力學方法,後來在十七世紀初開花結果,帶動了微積分的快速發展。
三、啟發性的論述
根據現存文獻記載,我們目前僅知阿基米德經常用無拘無束的想像力進行思考。希臘數學家因為受到季諾(Zeno,490-430B.C.)提出悖論的驚嚇,認為直覺是完全不可靠的,轉而尋求一個可以作為嚴密證明的途徑---幾何學。因此,正當希臘的數學家執著於理性證明時,阿基米德卻能藉助直觀的力學方法,作為證明的一部份。雖然,阿基米德仍是以當時數學家所認同的「窮盡法」(The Method of Exhaustion)作為嚴密的證明方法,他卻是利用力學方法幫助思考,進而發現定理的正確性,成為他特有的「發現的方法」。
阿基米德特有的「發現的方法」,是相當具有啟發性的論述。我們可以從文中的前兩個例子看出,他所利用的力學方法中,除了槓桿定理之外,也使用到相當於「微元」的技巧。他應用「微元」的概念論證許多面積和體積定理,亦即將平面和立體分別視為(無窮多的)直線與平面所組成,例如前文中介紹的《方法》的命題1,就是將三角形CFA視為平行MO的三角形內部直線所組成。阿基米德這樣無窮分割的想法和17世紀的克卜勒(J.Kepler,1571-1630)和卡瓦列里(B. Cavalieri,1598-1647)完全相同;甚至他提供獨特之「發現的方法」,從而利用了具物理直觀的「微元」論述,不但因此得到許多輝煌的成果,更是間接或直接的影響後來的積分學發展。
阿基米德在定理的嚴密論證前,所提供特有之「發現的方法」,不但在數學的發展上扮演了重要角色,也可以提供我們作為數學教學上的參考。阿基米德和同時代的數學家截然不同,對於直觀並沒有完全置之不理,反而透過依靠直觀的力學方法,提供了命題的發現方法,藉此更論述了許多關於面積和體積的定理。他這樣不受拘束的想法,正是他作為偉大數學家之一的最好佐證。誠然,一個有足夠空間發揮想像的人,才可能有最傑出的表現。所以,在我們的教學過程中,如果有學生和阿基米德一樣,提出與眾不同的想法,甚至和教科書中提供的做法大相逕庭時,只要是符合邏輯,我們都應該給予學生正面的評價才是。不但如此,我們在教學過程中,應提供學生多元思考的空間,並鼓勵學生多發揮自己的創意,因為在這樣的學習環境下,才有理由去期待我們的學生,和阿基米德一樣擁有偉大的想法。
註1:海伯格(Heiberg)於1906年發現的希臘手稿之一部分。
註2:阿里斯泰庫斯(Aristarchus)和歐幾里得的關於圓錐曲線的著作,參看阿基米德《論劈錐曲面體與旋
轉橢圓體》的命題3和《求拋物線弓形面積》的命題3有類似表達。
註3:阿基米德並未說明平面是如何由平行的直線所組成,也未提及平面是由無限或有限的直線所組成,因
此迴避了當時的希臘數學家所恐懼的無限概念。
註4:事實上,阿基米德除了按照力學方法所作的考察納入命題11、12之外,在命題13中也給出另一種他認
為仍不具說服力的解法。最後,在命題14增加了具有嚴密性的幾何證明。
註5:這一個命題同時解決了半圓柱即半圓的重心問題。因為處於原位置上的三角形GHM與同樣處於原位
置上的半圓PER,關於H點保持平衡。於是,若設GE上的點X為半圓OER的重心,則
(2/3)HO˙△GHM=HX˙半圓PER,即(2/3)HO˙HO2=
HX˙(1/2)π˙HO2,亦即HX=(4/3π)HQ。
參考書目:
Bell, E. T., 1998: 《大數學家》,台北:九章出版社。
Dunham, W., 1998: 《天才之旅》,台北:牛頓出版社。
Heath, T. L., 1998: 《阿基米德全集》,陜西:科學技術出版社。
Kline, M., 1983: 《數學史》,台北:九章出版社。
Meschkowski, H., 1964: 《偉大數學家的想法》,台北:南宏出版社。
Katz, J., 1993: A History of Mathematics: An Introduction. HarperCollins College Publishers.
Stillwell, J., 1989: Mathematics and Its History. NY: Springer-Verlag.