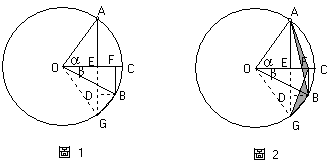
浙江大學數學系 汪曉群教授
拜讀HPM通訊,獲益頗多,對台灣中學數學教師們的良好素質及研究精神印象極深,同時深感通訊的生命力之強。
第三卷第一期(2000年元月)“和角公式的另一種表徵”一文中(三)、(四)兩段所證明的結論似應互換一下才對,可能是作者筆誤或排版者誤易兩圖所致。(編者註:感謝江老師指正,第三卷第一期已修正)
作者在文中提到:交大黃大原教授曾在一次演講中給出和角與和差化積公式的幾何證明。考察數學的歷史,我們發現16世紀法國數學家韋達(F.Vieta)曾給出和化積公式
Sinα+Sinβ=2Sin[(α+β)/2]Cos[(α-β)/2]
的幾何證明。
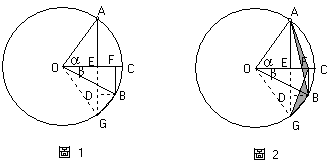
如圖1,設∠AOC=α,∠BOC=β是單位圓O的兩個圓心角。不妨設α和β為銳角,且α>β。過A、B分別作OC的垂線AE、BF,垂足為E、F。延長AE交圓O於G,連OG、BG。又作BD⊥AG,垂足為D。於是
Sinα+Sinβ=AE+BF=AD=AB˙Cos∠DAB。
而
∠DAB=(α-β)/2,AB=2Sin[(α+β)/2]
因此
Sinα+Sinβ=2Sin[(α+β)/2]Cos[(α-β)/2]。
順著韋達的思路,我們同樣可以證明其餘的和差化積公式。
(1)從圖1不難看出:∠AGB=(α+β)/2,又在等腰三角形OGB中,BG=2Sin[(α-β)/2],因此
Sinα-Sinβ=AE-BF=AE-DE=GE-DE=DG
=BG˙Cos∠DGB=BG˙Cos∠AGB
=2
Cos [(α+β)/2] Sin [(α-β)/2]。
(2) Cosα-Cosβ=OE-OF=-EF=-DB
=-BG˙Sin∠DGB
=-2Sin[(α+β)/2]
Sin [(α-β)/2]。
(3)為證明Cosα+Cosβ=2 Cos [(α+β)/2] Cos[(α-β)/2],我們在圖1中過圓心O作弦AB的垂線,
垂足為H,過H作HI⊥OC,垂足為I。則因AH=BH,故得EI=IF。因此
Cosα+Cosβ=OE+OF=2OI=2OH˙Cos∠HOI
而OH= Cos
[(α+β)/2],∠HOI=∠BAG=(α-β)/2,所以有
Cosα+Cosβ=2
Cos [(α+β)/2] Cos[(α-β)/2] 。
利用圖1我們還可以證明四個積化和差公式。
(4)在圖1中連接AF、GF,如圖2所示。因BF∥AG,故△AFB的面積和△GFB的面積相等,從而兩個
陰影三角面積相等。因此四邊形OAFG的面積和四邊形OABG的面積相等。於是我們有
Sinα˙Cosβ=AE˙OF
=四邊形OAFG的面積
=四邊形OABG的面積
=△OAB的面積+△OGB的面積
= [Sin(α+β)]/2+ [Sin (α-β)]/2
=[Sin(α+β)+ Sin (α-β)]/2。
(5)為了證明Cosα˙Sinβ=[Sin(α+β)-Sin (α-β)]/2,我們在圖1中過A、E、G分別作OB的垂線,
垂足分別為K、I、J,連GI并延長,交AK於L。如圖3所示。因E為AG之中點,故KI=IJ,LI=IG,
EI=AI/2。因此Rt△LKI
![]() Rt△GJI,因此GJ=LK。於是
Rt△GJI,因此GJ=LK。於是
Cosα˙Sinβ=OE˙EI/OE
=EI =AL/2
=(AK-LK)/2 =(AK-GJ)/2
=[Sin(α+β)-Sin (α-β)]/2。
(6)由圖3知,Cosα=OE,Cosα=OI/OE,故
Cosα˙Cosβ=OI
=OK+KI=OK+KJ/2
=(OK+OJ)/2= [Cos(α+β)+Cos(α-β)]/2 。
(7)在圖3中再作CM⊥OB,垂足為B。又設AK與OC交於N。如圖4所示。則Sinα˙Sinβ=AE˙CM。
因△AEN∼△OMC,故有AE/NE=OM/CM,即AE˙CM=NE˙OM。
但,OK/OM=ON/OC,即,OM=OK/ON,因此,
NE˙OM=OK˙NE/ON
= OK˙KI/OK=KI=(OJ-OK)/2
= [Cos(α-β)-Cos(α+β)]/2。