 Ah,
but my Computations, People say,
Ah,
but my Computations, People say,奧馬•海亞姆:阿拉伯數學家、天文學家、詩人及哲學家1
台師大數學研究所碩士班研究生
黃清揚
 Ah,
but my Computations, People say,
Ah,
but my Computations, People say,
Reduced the Year to better reckoning?—Nay,
′T was only striking from the Calender
Unborn To-morrow and dead Yesterday.
Rubaiyat LVII
啊!別人豈不說我的修曆使歲月好算?
不,唯有將未降生的明日,已逝去的昨天從曆書上消除,歲月才有改變。
《魯拜集》57
一、前言
西元九∼十二世紀可說是阿拉伯文明的黃金時代,此時希臘數學衰微,中亞細亞成為新的文化中心。西元766年,阿拉伯帝國的阿拔斯王朝建都巴格達,是為塞爾柱王朝(Seljuk)。之後於哈里發哈倫•拉西德(Hārūn al-Rashīd)統治期間(786-809),2在巴格達建立了一座圖書館,收藏了許多希臘古典時期的手抄本。而到了九世紀初,有一位熱心提倡學術的哈里發馬蒙(al-Ma’mūn,統治時期813-833),在他領導下,建立了後來延續200多年之久的學術研究機構—智慧宮(House of Wisdom),並廣泛網羅人才智庫。也由於統治者的鼎力支持,當時的阿拉伯國家善於吸取外來的文化,同時把大量希臘和印度的學術著作翻譯成阿拉伯文。於是,許多優秀的學者便在這樣的背景之下產生,且對後世數學及科學的發展有著不可磨滅的貢獻,其中之一,便是列名四位偉大阿拉伯科學家的奧馬•海亞姆。3
二、生平
奧馬•海亞姆(Omar
Khayyam或´Umar
al-Khayyāmī,約1048~約1131,全名Ghiyāth
al-Dīn Abu'l-Fath ´Umar ibn Ibrāhīm Al-Nīsaburī
al-Khayyāmī)或許是阿拉伯世界中最常被人們所提到的學者之一。他不僅是一位數學家,更是天文學家、詩人及哲學家,許多人對他詩集的認識更甚於其科學研究。其最著名的詩集—《魯拜集》(Rubaiyat),在經過英國詩人費滋傑羅(Edward Fitzgerald,1809-1883)於1859年之英譯後廣為流傳,至今此一詩集仍被傳頌。
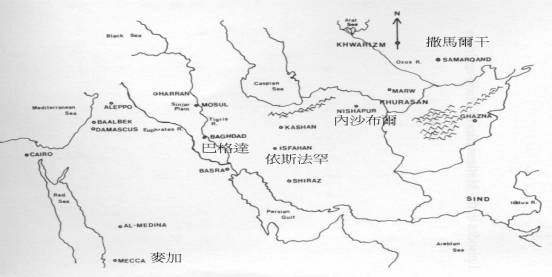
 奧馬•海亞姆生於波斯霍拉桑的內沙布爾(Nishāpūr,今伊朗境內的Khurasān),卒於同地(墓地見右圖)。他的名字al-Khayyāmī(帳棚製造者)透露出他的父親或先人可能從事過帳棚製造的生意。在奧馬•海亞姆出生前不久,賽爾柱土耳其人便征服了波斯並建立了不穩定的軍事帝國,而本文主角的一生與政治的起起落落可說是糾結在一起。我們並不太瞭解奧馬•海亞姆年輕時的活動,只知道他在Balkh(今阿富汗境內)求學,在17歲時便精通哲學的所有領域。1070年,他來到撒馬爾干(Samarkand,今烏茲別克境內),並在著名法學家(jurist)Abū
Tāhir的資助下寫下不朽的著作《代數學》。之後不久,在統治者Malik-Shah的邀請下,奧馬•海亞姆至依斯法罕(Isfaham,今伊朗境內)擔任當地天文台台長達18年之久,在那裡幾乎所有最好的天文學家都聚集在此天文台工作。由於統治者的大力支持,奧馬•海亞姆在學術方面的工作相當順利。這期間他寫下許多經典著作,並於1079年主導過曆法改革。1092年之後,因為一連串的政治事件,再加上有人指控他的四行詩中出現對傳統宗教的不滿,奧馬•海亞姆便逐漸失去統治者的贊助及支持。為了澄清無神論的指控,奧馬•海亞姆晚年更曾籌備麥加朝聖之旅。
奧馬•海亞姆生於波斯霍拉桑的內沙布爾(Nishāpūr,今伊朗境內的Khurasān),卒於同地(墓地見右圖)。他的名字al-Khayyāmī(帳棚製造者)透露出他的父親或先人可能從事過帳棚製造的生意。在奧馬•海亞姆出生前不久,賽爾柱土耳其人便征服了波斯並建立了不穩定的軍事帝國,而本文主角的一生與政治的起起落落可說是糾結在一起。我們並不太瞭解奧馬•海亞姆年輕時的活動,只知道他在Balkh(今阿富汗境內)求學,在17歲時便精通哲學的所有領域。1070年,他來到撒馬爾干(Samarkand,今烏茲別克境內),並在著名法學家(jurist)Abū
Tāhir的資助下寫下不朽的著作《代數學》。之後不久,在統治者Malik-Shah的邀請下,奧馬•海亞姆至依斯法罕(Isfaham,今伊朗境內)擔任當地天文台台長達18年之久,在那裡幾乎所有最好的天文學家都聚集在此天文台工作。由於統治者的大力支持,奧馬•海亞姆在學術方面的工作相當順利。這期間他寫下許多經典著作,並於1079年主導過曆法改革。1092年之後,因為一連串的政治事件,再加上有人指控他的四行詩中出現對傳統宗教的不滿,奧馬•海亞姆便逐漸失去統治者的贊助及支持。為了澄清無神論的指控,奧馬•海亞姆晚年更曾籌備麥加朝聖之旅。
他的著作,除了《魯拜集》對後世有重大的影響外,數學方面的成就也是不可忽視的。諸多數學作品中,最著名的可說是《代數學》一書。
三、《代數學》
《代數學》,原書名為『還原與對消問題論證』(Risāla fi΄l-barāhin alā masā΄il al-jabr wa΄lmuqābala)。本書完成於1100年左右,奧馬•海亞姆將代數定義為『解方程的科學』(a “scientific” art),也因此進一步推進了方程理論。為了方便解三次方程,奧馬•海亞姆採取與阿爾•花拉子模相似的作法,4首先考慮所有形式的三次方程式。又因為他只接受正根,係數也限於正數,因此最終他將三次方程式歸結為14類,分別是:二項式一個(x3=d),三項式六個(x3+cx=d, x3+d=cx, x3=cx+d, x3+bx2=d, x3+d=bx2及x3=bx2+d),四項式七個 (x3+bx2+cx=d, x3+bx2+d=cx, x3+cx+d=bx2, x3=bx2+cx+d, x3+bx2=cx+d, x3+cx=bx2+d及x3+d=bx2+cx)。然後奧馬•海亞姆對每一類的方程式都作仔細的分析,並引進希臘人曾經使用過的方法 — 兩個圓錐曲線的交點,來證明其結論是正確的,最後並討論在什麼情況下,此三次方程式無解或多個解。值得注意的是,在討論三次方程式時,奧馬•海亞姆依然採取古希臘「齊次」的觀點,亦即三次方程式中的每一項必須對應一個立體。以下我們來看看奧馬•海亞姆對x3+cx=d的處理。
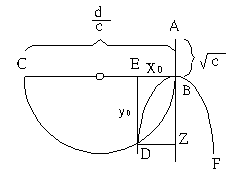 因為x代表立方體的一個邊長,c必須代表面積(正方形),d則為立體。為了求解,奧馬•海亞姆取
因為x代表立方體的一個邊長,c必須代表面積(正方形),d則為立體。為了求解,奧馬•海亞姆取
![]() ,即
,即
![]() 為面積為c之正方形的一邊。接下來作
為面積為c之正方形的一邊。接下來作
![]() ,使得
,使得
![]() 或
或
![]() 。下一步將
。下一步將
![]() 延長至Z,並作一條以B為頂點、BZ為軸、參數為
延長至Z,並作一條以B為頂點、BZ為軸、參數為
![]() 的拋物線,其方程式為
的拋物線,其方程式為
![]() 。之後,在
。之後,在
![]() 作一個方程式為
作一個方程式為
![]() 或
或
![]() 的半圓。從圖上可知,這兩條圓錐曲線交於D,而他的x軸長(
的半圓。從圖上可知,這兩條圓錐曲線交於D,而他的x軸長(
![]() )即為此三次方程式的解。
)即為此三次方程式的解。
奧馬•海亞姆證明其解的正確性如下:若
![]() 、
、
![]() ,則
,則
![]() 或
或
![]()
並且
![]() 或
或
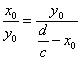 ,
,
所以
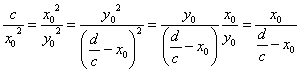 。
。
從而
![]() ,x0即為所求。在此,奧馬•海亞姆指出這一類的方程在原點之外一定有一根(交點),而原點並不是這方程式的解。
,x0即為所求。在此,奧馬•海亞姆指出這一類的方程在原點之外一定有一根(交點),而原點並不是這方程式的解。
對於其他類型的三次方程式之討論,奧馬•海亞姆都是用類似的方法來進行的。5對於那些正根並不一定存在的情形,他給出了幾何條件:根的存在與否,端視兩圓錐曲線是否交於一點、兩點或不相交。然而,對x3+cx=bx2+d這一類的方程式,他並沒有發現存有三根的可能性。而對於解與係數的關聯性,奧馬•海亞姆也僅在少數的情況之下才加以討論。
奧馬•海亞姆三次方程的幾何理論可說是他最成功的研究成果,帶給後世相當可觀的影響。納西爾丁(Nasīr al-Dīn al-Tūsī, 1201-1274)基於奧馬•海亞姆的成果繼續往前推進,而西歐數學家在這方面的研究,則是在笛卡爾(Descartes, R., 1596-1650)之後的故事了。除了在三次方程式的貢獻之外,奧馬•海亞姆對幾何學的探討也至關重要。
四、幾何學
 1077年,在奧馬•海亞姆提出曆法改革前兩年,他完成了另一項重要的著作《對歐幾里德幾何原本設準之問題的評論》(Sharh
māashkala min musādarāt kitāb
Uqlīdis, Commentary on the Problematic Postulates of the Book of
Euclid)。本書討論到兩個相當重要有關於幾何基礎的問題,其中之一為《幾何原本》第五設準(平行設準)問題。奧馬海•亞姆打算經由前面四個設準,來證明出第五設準,如此一來,他就只需要四個設準,就能推導出後面的所有命題了。這個問題在較早前已被塔比伊本庫拉(Thābit
ibn Qurra,約826-901)以及伊本海塞姆(Ibn
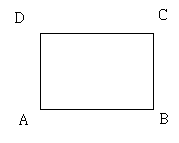
al-Haytham,965-1039)研究過。6奧馬•海亞姆顯然不滿意他們的研究,他從四邊形ABCD著手(如右圖),CB與DA為兩個長度相同的線段且皆垂直AB。奧馬•海亞姆認識到為了要從其它設準來證明平行設準就需要證明角C及角D為直角,因此,他分別假設角C、D為銳角、鈍角及直角,而前兩者都會得到『矛盾』。有趣的是,這種處理方式與非歐幾何學有密切的關係,因為接受前面兩種假設為真時,最終都會導致非歐幾何學的誕生。顯然奧馬•海亞姆當時無意於此,不過,他的成就的確影響了後來相關數學的發展。一百五十年後,納西爾丁接受了奧馬•海亞姆的觀點,並且在這方面的研究做出了貢獻。而納西爾丁的研究更影響歐洲十七、十八世紀的幾何學家,譬如1651年、1663年沃利斯(John
Wallis,1616-1703)討論歐幾里德的設準問題時,便引用了納西爾丁的著作。
1077年,在奧馬•海亞姆提出曆法改革前兩年,他完成了另一項重要的著作《對歐幾里德幾何原本設準之問題的評論》(Sharh
māashkala min musādarāt kitāb
Uqlīdis, Commentary on the Problematic Postulates of the Book of
Euclid)。本書討論到兩個相當重要有關於幾何基礎的問題,其中之一為《幾何原本》第五設準(平行設準)問題。奧馬海•亞姆打算經由前面四個設準,來證明出第五設準,如此一來,他就只需要四個設準,就能推導出後面的所有命題了。這個問題在較早前已被塔比伊本庫拉(Thābit
ibn Qurra,約826-901)以及伊本海塞姆(Ibn
al-Haytham,965-1039)研究過。6奧馬•海亞姆顯然不滿意他們的研究,他從四邊形ABCD著手(如右圖),CB與DA為兩個長度相同的線段且皆垂直AB。奧馬•海亞姆認識到為了要從其它設準來證明平行設準就需要證明角C及角D為直角,因此,他分別假設角C、D為銳角、鈍角及直角,而前兩者都會得到『矛盾』。有趣的是,這種處理方式與非歐幾何學有密切的關係,因為接受前面兩種假設為真時,最終都會導致非歐幾何學的誕生。顯然奧馬•海亞姆當時無意於此,不過,他的成就的確影響了後來相關數學的發展。一百五十年後,納西爾丁接受了奧馬•海亞姆的觀點,並且在這方面的研究做出了貢獻。而納西爾丁的研究更影響歐洲十七、十八世紀的幾何學家,譬如1651年、1663年沃利斯(John
Wallis,1616-1703)討論歐幾里德的設準問題時,便引用了納西爾丁的著作。
另外一個奧馬•海亞姆所考量的問題是比(ratios)。而他的成就有兩方面,一是將比例(proportion)的定義表達得更為詳盡;另一則是將數的觀念擴大至包含量與量的比。在歐幾里德《幾何原本》第五卷定義5中,兩比例相等的定義如下:
有四個量,第一量比第二量與第三量比第四量稱做有相同比,如果第一與第三個量取任何相同倍數,又對第二與第四個量取任何相同倍數,而第一與第二倍量之間依次有大於、等於或小於的關係,便有第三與第四倍量之間相對應的關係。7
也就是說:a與b是相同量且c與d也是相同量,若(1)ma<nb時,mc<nd(2)ma=nb時,mc=nd(3)ma>nb時,mc>nd成立,就稱a:b = c:d(m、n為任意正整數)。奧馬•海亞姆並不認同這個定義,因為我們不可能去測試所有的正整數,而且對比的運算也會出現問題。所以,他以如下定義替換(用現代語言):
若
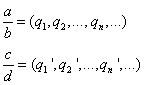
則
![]() 的條件是
的條件是
![]() (對可公度比來說,k是有限)。這樣一來,奧馬•海亞姆就大大提高了『比』的可運算的程度了。
(對可公度比來說,k是有限)。這樣一來,奧馬•海亞姆就大大提高了『比』的可運算的程度了。
再者,希臘人認為不可公度量就不能稱為數,譬如正方形對角線與邊長的「比」(
![]() :1)。這個概念,到了奧馬•海亞姆則是被解放出來了,他直接了當的說任意量之比(不論可公度或不可公度)皆是數。如此,他便能隨心所欲地處理無理數,不再被不可公度量的複雜運算綁得礙手礙腳了。如同前面所提平行設準對後世的影響一樣,歐洲數學家同樣地從納西爾丁著作中,得到奧馬•海亞姆的啟發。無論如何,奧馬•海亞姆影響了歐洲數學的發展,殆無疑問。
:1)。這個概念,到了奧馬•海亞姆則是被解放出來了,他直接了當的說任意量之比(不論可公度或不可公度)皆是數。如此,他便能隨心所欲地處理無理數,不再被不可公度量的複雜運算綁得礙手礙腳了。如同前面所提平行設準對後世的影響一樣,歐洲數學家同樣地從納西爾丁著作中,得到奧馬•海亞姆的啟發。無論如何,奧馬•海亞姆影響了歐洲數學的發展,殆無疑問。
五、結論
 經由本文有關奧馬•海亞姆的故事及成就之介紹,筆者希望能讓大家認識到阿拉伯數學對世人所做出的貢獻。事實上,阿拉伯數學吸收了古希臘、印度、中國和本地區的數學,融會東、西方的長處於一身,最後發展出獨特的風格。這種評價套在奧馬•海亞姆身上也不例外,8而他原創性的著作對西歐數學的發展,更是不可磨滅。可惜,阿拉伯數學對西方的影響似乎被諸多西方史家刻意忽視下長期地被扭曲了,9或許這正是西方宗教及民族自尊心發酵之後的結果吧!目前,東、西文化正處於對立與衝突的緊張關係之中,或許也正是讓我們多方瞭解神秘面紗背後的笑容與智慧的最佳時機吧!最後,請容許筆者以奧馬•
經由本文有關奧馬•海亞姆的故事及成就之介紹,筆者希望能讓大家認識到阿拉伯數學對世人所做出的貢獻。事實上,阿拉伯數學吸收了古希臘、印度、中國和本地區的數學,融會東、西方的長處於一身,最後發展出獨特的風格。這種評價套在奧馬•海亞姆身上也不例外,8而他原創性的著作對西歐數學的發展,更是不可磨滅。可惜,阿拉伯數學對西方的影響似乎被諸多西方史家刻意忽視下長期地被扭曲了,9或許這正是西方宗教及民族自尊心發酵之後的結果吧!目前,東、西文化正處於對立與衝突的緊張關係之中,或許也正是讓我們多方瞭解神秘面紗背後的笑容與智慧的最佳時機吧!最後,請容許筆者以奧馬•
海亞姆的另一首詩來結束本文:
The Moving Finger writes, and,
having writ,
Moves on: nor all thy Piety nor Wit
Shall lure it back to cancel half a Line,
Nor all thy Tears wash out a Word of it.
Rubaiyat LXXI
揮動的手指書寫且書寫完成,繼續揮動;
既不是你的智慧亦不是你的虔誠能把它半行更改,
你所有的眼淚亦不能把它一字洗清。
《魯拜集》71
註解:
1. 這裡所稱的阿拉伯數學,是指用阿拉伯文為主要文字寫成的數學著作所代表的數學,其中的學者並非全然是伊斯蘭教徒。
2. 哈里發(caliph)為伊斯蘭教先知穆罕默德逝世後,繼續執掌政教大權者的稱謂,原意為代理者、繼任人。西元1258年,阿拔斯王朝最後一位哈里發穆斯台爾綏姆被蒙古旭烈兀軍隊殺害後,『哈里發』當作伊斯蘭國家最高政治和宗教領袖的職位,基本上已不復存在。
3. 其餘三位分別是阿爾•花拉子模(Al-Khawārizmī,約780-
850)、阿爾•比魯尼(al-Bīrūnī,973-約1055)、阿爾•卡西(al-Kāshī,約卒於1436),見Berggren
(1986), pp. 5-21。
4. 阿爾花拉子模將二次方程式分為六種。
5. 例如解x3 + bx2 = b2c用拋物線與半圓;解x3 + ax2 = c3用拋物線與雙曲線;解x3 + ax2 + b2x = b2c則用橢圓與雙曲線。
6. 早在希臘時代就有許多數學家對這個問題提出討論,如托勒密(Ptolemy,約110-約170)與普羅克洛斯 (Proclus,約412-485)。
7. “Magnitudes are said to be in the same ratio, the first to the second and
the third to the fourth, when, if any equimultiples whatever be taken to of the
first and third, and any equimultiples whatever of the second and fourth, the
former equimultiples alike exceed, are alike equal to, or alike fall short of,
the latter equimultiples respectively taken in c0rresponding order.”(Heath (1956), p.114)
8. 事實上,奧馬•海亞姆對印度數學並不陌生,因為他曾引用與印度數學相關的著作。其中有兩本書的作者提出了從自然數來解平方及三次方根的方法,分別是Kushyār
ibn Labbā al-Jīlī(971-1029)所著的《印度計數法則》(Fīusul hisāb al-hind,
Principles of Hindu Reckoning)及`Alī
ibn Ahmad al-Nasawī(fl.
1025)所著《充分瞭解印度計數所需具備的事物》(Al-mugnīcfı,l-hisāb
al-hindī, Things Sufficient to Understand Hindu Reckoning),這些內容與印度數學傳統的進路並不相同。根據Dictionary
of Scientific Biography的說法,其來源是中國數學,這仍有待考證。
9. Morris Kline《數學史》(Mathematical Thought from Ancient to Modern Times)中便有許多這樣的觀點。
參考文獻
李文林主編 (2000).《數學珍寶》,台北:九章出版社。
梁宗巨 (1992).《數學歷史典故》,台北:九章出版社。
Omar Khayyam (1990).《魯拜集》(孟祥森譯),台北:遠景出版事業公司。
Kline, Morris (1983).《數學史—數學思想的發展》(林炎全等譯),台北:九章出版社。
Berggren, J. L. (1986). Episodes in the Mathematics of Medieval Islam. New York: Springer-Verlag.
Calinger, Ronald(ed.)(1995). Classics of Mathematics. Englewood Cliffs: Prentice-Hall, Inc.
Gillispie, Charles Coulston (editor in chief) (1981). Dictionary of Scientific Biography. New York: Charles Scribner’s Sons.
Heath, Sir Thomas L. (1956). The Thirteen Books of Euclid Elements (Vol. 2). New York: Dover.
Katz, Victor J. (1993). A History of Mathematics: An Introduction. New York: HarperCollins College Publishers.
Rashed, Rshdi, translated by A. F. W. Armstrong (1994). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Dordrecht: Kluwer Academic Publishers.
Struik, Dirk J. (1987). A Concise History of Mathematics. New York: Dover.