中文版                                                                    英文版

書名：毛起來說三角                                      Trigonometric Delights

作者：Eli Maor

出版者：天下遠見出版股份有限公司         Princeton University Press

出版日期：2000年9月30日                            1998

頁數：294頁 236+14

定價：新台幣250元

ISBN：957-621-732-6                                      ISBN：0-691-05754-0

一、 前言

        身為一位數學教師，每當課程進行到三角函數時，繁多的三角公式頓時湧現於眼前，加由於運算技巧的不足，學生常因此望之卻步，學習意願一落千丈。教材內容編寫的枯燥是個因素，相關題材的補充資料難尋是另一個問題，常令人在教學的引導上，有巧婦無米可炊之嘆。因此，當筆者由洪萬生教授處，得知Maor有本關於三角函數的著作，便經由亞馬遜網站購得此書，作者的文筆相當流利，相當具有可讀性，同時，書中內容包羅萬象，足見作者對此一主題資料收集的功力。後來又見天下出版此書的中文版，遂有意推介給對三角函數題材有興趣的同好知曉，讓更多人重新去體會三角函數的風貌。

新數學對幾何學及三角學的傷害最大。[1]理工科課程中最關鍵的三角學，成為改革的犧牲者。它打著嚴謹的名號，形式化的定義及冗長的邏輯推導，取代對它的實質的了解。……用將實數映成(onto)到〔-1，1〕區間的函數來定義正弦和餘弦，取代用三角形邊的比例或單位圓在x軸和y軸上的投影的幾何脈胳來定義。集合的符號及語言占據所有的討論，使得一個相當簡單的課題，變成無意義的形式主義。(Maor 1997, p.xii)

因此，造成學生認為「三角學是加了桂冠的幾何學，再加上計算的苦刑」。[2]Maor寫作本書試圖反駁這個說法，在取材的廣度上，作者除了引入三角學歷史發展的過程外，也選擇甚多三角學中有趣的例子，或是與其他領域相關(如地圖繪製)的題材。在讀者設定上，也以高中生和大學生為主，因此內容的深度多半利用基本的代數與三角學知識便可理解，討論的重點也侷限在平面三角學上。

        此外，Maor將一些相關的數學史傳記或材料補充於章節之後，共有八篇之多。雖然這些文章多半都是根據二手文獻改寫，但值得一提的是，頗多是「非主流」的數學家的生平與貢獻(如雷吉蒙塔努斯 (Regiomontanus), [3]棣美弗(Augustus De Moivre)，阿涅西(Maria Gaetana Agnesi))，或是在數學史的書中少見的資料(如棣美弗與牛頓的關係，維埃塔(Viete)如何利用三角函數解出四十五次的方程式的正根)，[4]可見Maor在寫作的選擇上有其「另類」的考慮。再來就本書內容作一說明。

二、內容簡介

        本書共有十五章及四個附錄，[5]就內容可分成下列幾項：(1)三角學發展的歷史(前言，第一章至第四章)；(2)三角學的應用(第五章及第十三章)；(3)平面三角學中有趣的題材(第六章至第十二章)；(4)三角學進一步的延拓(第十四章及第十五章)。由章節分量的安排可見，作者並無意讓本書成為三角學的發展歷史的專書，倒是極力想推介一些三角學中被人遺忘，但又非常美麗易懂的公式或性質，期許讀者能重拾對三角學的興趣與熱情。

(1) 三角學的發展歷史

        前言中，Maor由一位埃及的古代書記阿美斯(Ahmes)開始談起，據信萊因德紙草書(Rhind Papyrus)是他根據更早的文獻所抄下。紙草書是以問題集的形式呈現，其中第56題至60題，便是有關金字塔的測量問題，由此我們可以看出埃及人已有簡單的三角學概念，能利用金字塔底邊長的一半與塔高的比例，來保持底面與邊面的夾角(傾斜度)固定。可見三角學的概念萌發甚早，也非常的實用，但是真正將它抽象成數學概念，則是希臘人的工作。接著第一章是介紹角的概念源起及單位的演變，一般認為角的單位「度」是巴比倫人制定，為何一個圓是360度，原因則無一定論。至於另一個度量單位「弧度」的使用，Maor認為其可能的原因有兩個：一來使得角的公式變得較為簡單(如弧長，扇形面積的公式)，二來角度的大小用弧度表示，很小的角度會與它的正弦值近似，也就是，因此在微積分中多以弧度為單位。

        再來第二章的重點是介紹托勒密(Ptolemy)的弦表，此表出現在他的著作《大成》(Almagest)第一冊第十章及第十一章。他將圓的弦長看成「弦所對應的圓心角的函數」，與正弦函數的定義相符，因此，此一的弦表就是正弦函數表。事實上，托勒密的工作主要是繼承希巴爾卡斯(Hipparchus)的研究成果。當時希臘人的主要興趣在天文觀測，為了因應計算的需求，才會編製弦表來求解任意的圓內接三角形。[6]值得注意的是，托勒密的弦表精確到六十進位制的第二位(即1/3600)，並且給出相鄰數值間的平均增加量，方便內插計算之用。現在我們熟知的六個三角函數的由來，則是作者在第三章想交代的。例如，正弦函數的概念發生很早，印度的數學家接續托勒密的成果，完成進一步的改良工作。經由阿拉伯人再傳回歐洲時，正弦函數被寫為sinus，至於再簡寫成sin的符號則是岡特(Gunter)所採用。Maor在此章的材料敘述的安排上，略顯得雜亂。閱讀本章時，切記函數概念和函數符號的使用或演進，是必須分開的，不然將陷入混淆的年代錯置中。此外，細心的讀者會發現第三章交代第一個使用縮寫並且能保持一致性的數學家，是英國數學家兼測量師諾伍德(Norwood, 1631)，而第四章卻又提到十七世紀前半，有三個英國人對三角學貢獻良多，其中奧特雷德(Oughtred, 1657)首先有系統地使用縮寫符號代表三角函數。仔細比較文中關於兩人所用符號的說明差異不大，為何令人覺得說法不一，原因何在？Maor並未說明。經筆者查閱發現：諾伍德首先有系統地的使用縮寫符號，但奧特雷德是當時英國最有影響力的數學書籍作者，像牛頓、[7]華理斯(John Wallis)都是他的讀者，[8]因此他的重要性不言而喻。[9]

        至於第四章則介紹三角學的解析化發展，Maor認為埃維塔最早將代數方法運用在三角學中，為三角學滲入解析的特質；加上解析幾何的出現，更助長代數的發展。另一個重要因素則是數學所描述的對象有了改變，古典的三角學主要是應用在天體上，因此首重球面三角學。而十七世紀開始，重心轉移到力學的應用上，例如鐘擺及彈簧的振動問題，而這些描述週期現象的問題，使得三角函數有更大揮灑的空間，也讓三角學由函數表的編纂，變成各三角函數間性質的探討。加上寇茨(Cotes)、棣美弗及歐拉(Euler)等人的研究，將複數融入三角學之中，使三角學與分析學相結合。因此三角學與三角形漸行漸遠，到了十八世紀，開始將三角函數定義成純數字，而非三角形的三邊長的比值。[10]更由於「振動弦」問題，引出解的兩種形式爭論，最後歸結到在傅立葉(Fourier)所証明的定理：「只要函數在某個區間中被視為週期函數時，就可以被表示成正餘弦函數的級數和」，也使得三角學成為十九世紀分析學上研究週期函數的有力工具。

(2) 三角學的應用

        Maor在第五章中回顧人類最早使用三角學的歷史-「量天度地」，由阿里斯塔克斯(Aristarchus)測量太陽、地球與月球彼此間的距離的方法談起，到希巴爾卡斯改良測量方式，及埃拉托斯特尼(Eratosthenes)估計地球的圓周長，重現了希臘人對量度天體的努力。這種測量概念後來逐漸演變成測地學，其測量方法被稱為「三角分割」，藉由地表的測量決定地球的形狀。由於地球形狀的議題牽涉到牛頓的重力理論與笛卡兒的渦動理論的論辨，並且引出英國與法國的國家尊嚴之爭。使得十八世紀，由法國開始引起一股測地的風潮，蔓延到整個歐陸。可見外在因素是會影響科學活動的進行。

        接著十三章則是轉向地圖學中的所使用的三角學，Maor簡介了幾種製圖所用的投影方法以及其中所使用的三角學知識，如圓柱投影、球極投影等。但不論是何種投影法，都無法符合當時航海的需求，這個難題最後由麥卡托(Mercator)所發明的投影法所解決。但麥卡托並未清楚交代他的製圖原理，因此在當時他的製圖法無法得到認同，後來由萊特(Wright)利用數值積分的方法，反覆求取每一分弧度所加上的正割值，列出經度0°到75°的結果，驗証麥卡托的原理，其製圖法才得以推廣。

(3) 平面三角學中有趣的題材

        筆者覺得Maor在本書中最大的貢獻便是此一部份素材的搜集，對於教學上頗有幫助。譬如第六章，由「圓中一弧所對的圓心角等於圓周角的兩倍」的定理，推而証明正弦定理及倍角定理，給我們一個不同於現行教材利用面積相等的証明方法。這樣將任意三角形看成圓的內接三角形的方式，是比較符合希臘人的看法。把正弦定理看成與圓有關，能給我們更多的幾何意義上連結。再來Maor透過托勒密定理，[11]給出畢氏定理的另一種証明；也証明出正弦函數的和角公式。讓我們進一步了解托勒密定理在三角學上的重要性，並非是我們習題中一個不起眼的問題罷了。第七章的內容，對我們是比較陌生的，作者介紹外擺線與內擺線的參數方程式及性質。

        第八章主要介紹一個三角級數和公式

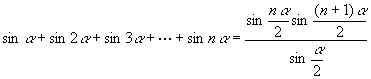
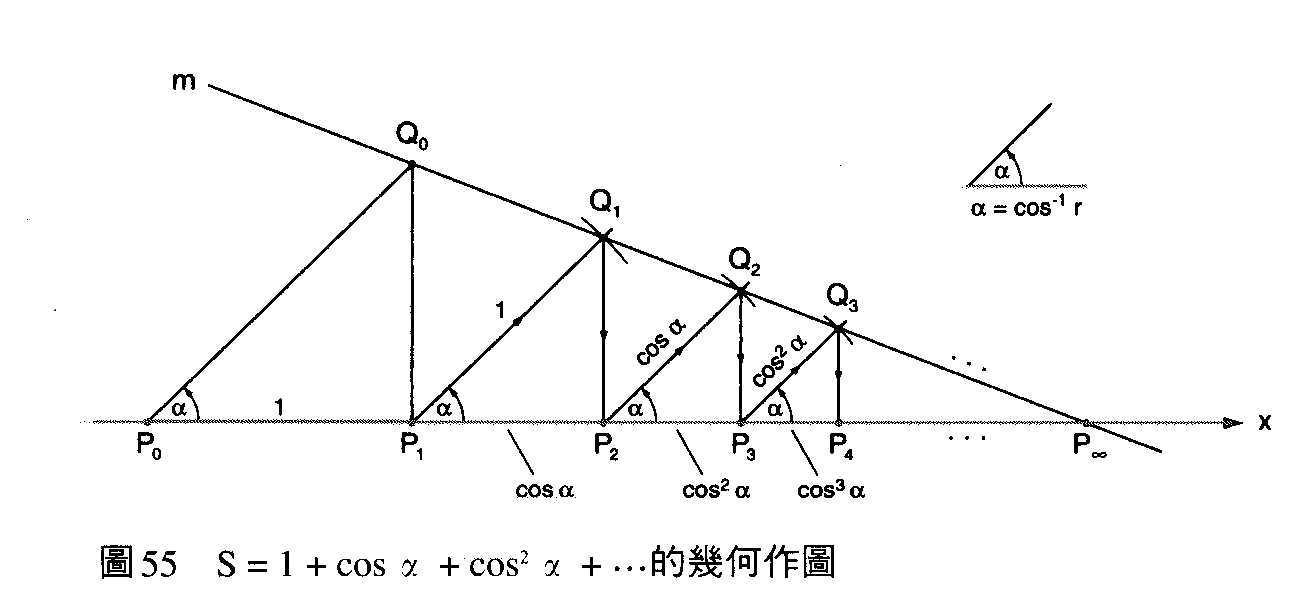
有趣的是，Maor由高斯求級數1加到100的小故事談起，引入相仿高斯的想法，推導此一級數公式的想法，最後再利用幾何作圖，讓我們了解這個級數公式的幾何意義。接著第九章是有關無窮等比級數的論述，最精彩的部份是「任何一個收斂的無窮等比級數，均可用直尺和圓規以幾何方法作出，並可由圖形求和」，筆者尤其推薦此章，Maor 試圖想告訴讀者對三角學的理解，不應只是繁複的三角函數計算的代數面向，它有著極為美麗可見的幾何面向(此想法散見各章)。其基本想法是-1到1之間的任意實數，均可與0°到180°間的餘弦函數一一對應，因此級數和可看成，如此一來，我們就能由幾何作圖來求和。(如右圖為銳角的情形)

        第十章與第十一章，是有關函數的種種，除了外，還有一些相關性質與應用，例如是某種三維空間的世界投影到二維空間中的比例函數；或是歐拉曾發現這個無窮乘積的式子，Maor當然也說明此乘積的幾何証明和幾何意義。第十二章的內容，Maor則是留給函數，雖然在三角學的發展上，一直讓人覺得正餘弦函數的重要性遠超過正切和餘切函數。事實上正切函數的概念起源很早，在投影問題中便已出現。像維埃塔就曾提出正切定理，雖然現代的課本已經不提，但在沒有計算機的輔助求解三角形時，這定理可比餘弦定理更容易利用對數來運算。此外，的展開式與二項式定理關係密切；還有經由的部份分式，Maor重新驗証許多歷史上與π有關的著名級數公式，這些都是在一般教材中甚難得知的部份。

(4)三角學進一步的延拓

        Maor深覺三角學的歷史中，「有三項發展特別顯著，基本上改變了整個課題：托勒密的弦表，使得三角學成為實用的計算科學；棣美弗定理及歐拉的公式，使得三角學與代數和分析學相融合；再來就是傅立葉定理。」(見Maor 1997, p. 198或中文版251頁)不難了解Maor撰寫第十四章與第十五章的用意。在第十四章中，透過歐拉的公式，我們能找到(雙曲餘弦)與雙曲正弦)的關係式，以及熟悉的三角公式，也能找到相對應的雙曲公式。因此，我們能將三角學推廣到複數平面上。最後一章傅立葉定理，則在簡介傅立葉的生平及說明傅立葉定理的梗概與應用，為全書畫下句點。雖然筆者能體會作者為求完整性，而安排了最後兩章，但由於讀者設定及題材難度的緣故，只能點到為止，內容相當簡略，略顯得美中不足。有興趣者不妨參閱相關數學書籍。

三、結論

        綜觀全書作者在題材選擇和舖陳上，仍然遵循著三角學發展的歷史架構，儘管在三角學發展的歷史上，材料的剪裁稍顯零亂。尤其，省去球面三角學的發展與相關題材的作法，則是讓人深覺可惜。然而，在作者的生花妙筆下，書中的各種主題相當平易近人。其實，Maor扭轉三角學只是由一堆三角公式所堆砌出的刻板印象其用心令人感動。他在每一章節儘可能將三角學與幾何學緊緊相扣，為三角公式找到幾何解釋與論証。這樣的努力值得我們喝采！基於教學經驗，筆者深刻地體會，如何讓學生能「看見」一個數學式子的意義是非常困難的。若能藉由幾何圖解，往往比較能讓學生容易感受。Maor的現身說法，無疑地開啟一條值得大家共同努力的道路。在古代數學文本被遺忘的舊有風貌，若能適當地賦予意義重新詮釋，想必對於教學工作的啟發有著莫大的助益！

        最後，筆者覺得必須為譯者的用心說上幾句，本書的中文版相當流暢，也能扣住作者的本意，除了一些數學家的人名或著作的譯名與慣用的稱呼有些出入。值得一提，譯者對於人名翻譯都會附注原文，這是相當棒的作法。如果數學著作也能附上原文，那就更加完善了。有幾處明顯錯誤藉此提出，107頁的Stirling公式應為，及175頁表4下方的一行文字應為“由北極到赤道的距離恰為赤道圓周長〔書中誤譯為半徑〕的四分之一” 。至於令人詬病專業名詞誤譯的問題並未出現。這應該與譯者本身的數學專業有關，或許能提供讀者在購買科普翻譯書籍時一個參考的指標。

數字的故事告訴了我們什麼？
~~評論《毛起來說e (e: The Story of a Number)》

西松高中 蘇惠玉

中文版                                                                                         英文版

書名：毛起來說e                                                                         e: The Story of a Number

作者：Eli Maor

出版社：台北：天下遠見                                                          Princeton University Press

出版資料：2000年第一版，共304頁，定價250元。             1994

國際書碼：ISBN 957-621-743-1                                                 ISBN 0-691-03390-0

        筆者上學期在參與國科會研究計畫「古文本在數學課堂中的應用」時，選定了「圓」當我教學上的主題，主持人洪萬生教授推薦我看To Infinity and Beyond: A Cultural History of the Infinite 這本書，作者即為E. Maor。這本書的內容非常的生動有趣，同時包含許多的數學人文活動面向，讓人印象深刻，也因此開始注意到Maor這個作者的一系列書籍。於是，我們這一群人上網買了Maor的另兩本書：e: The Story of a Number 及Trigonometric Delights 。在我們還來不及將英文版讀完之時，想不到天下文化已經發行了中文版了（《毛起來說e》與《毛起來說三角》）！在語言的便利之下，當然先讀中文版囉！

        在高中舊課程的最後一年的課程中，高三學生必須要學習微積分，學習指數與對數的微分當然也是勢所必然！但是，在在一般教科書中，e這個數字只是冷冰冰的定義而已。所以，我試圖從《毛起來說e》這一本書中，尋求一些教學上的資源。而在教完這個單元的現在，我可以很欣慰的表示說：收穫良多。

作者簡介：Eli Maor, 芝加哥羅耀拉大學(Loyola University)數學史教授，多年來於許多數學和數學教育期刊發表過文章。

譯者簡介：鄭惟厚，台灣大學數學系畢業，美國愛荷華大學統計博士。現任淡江大學數學系教授。

        Maor 在序言中提到，要更正學生對數學的負面態度，「講點數學歷史是很好的方法」，而這本書就是從這種教學法衍生出來的。同時，他認為π的歷史書寫中，沒有比P. Beckmann的 A History of π更好的書，而在e的歷史書寫中，還沒有可媲美的書出現。他似乎有個雄心壯志，想要在數字的歷史書寫中，佔有一席之地。

        這本書中總共有15章，8個附錄。茲轉述如下：

第1章 納皮爾：對數的創造者

第2章 迎接對數

第3章 財務問題

第4章 極限

第5章 微積分的源起

第6章 突破的前奏

第7章 求雙曲線的面積

第8章 一門新科學的誕生

第9章 大爭論

第10章 ：等於自己導數的函數

第11章 ：神奇螺線

第12章 ：懸著的鏈子

第13章 ：「最有名第18章 的公式」

第14章 ：想像成真

第15章  但它到底是怎樣的一個數呢？

附錄1 納皮爾對數的一些補充說明

附錄2 當時，極限值的存在

附錄3 微積分基本定理的啟發式推導過程

附錄4 當時，與之間的關係

附錄5 對數函數的另一種意義

附錄6 對數螺線的兩個性質

附錄7 雙曲函數中的參數ψ如何解釋

附錄8 e展開到小數一百位

從目錄的編排來看，就可以知道Maor這一本書的安排順序。因為這個數字，牽涉到對數、極限與微積分的觀念，所以Maor將這些觀念的發展，以時間為縱軸來敘述，再佐以相關的數學史上的人物、典故為橫軸，間夾雜以一些風雅的e的趣聞來點綴。

        Maor以對數的起源當故事的開頭。在第1章、第2章中，他首先敘述了納皮爾（1550-1617）的生平事蹟。然後再詳細地講解納皮爾對數產生的作法。因為在納皮爾的對數中，納皮爾選取的底為，即，其中L為N的納皮爾對數。當然，我們可以發現這個N的定義方式與現今的定義幾乎是等價的。所以，Maor說：「事實上，納皮爾還差一點發現了這個數。」（p.11注14）第2章中，他接著說明對數發明後大受歡迎的程度。以及後續的改良。

        在第3章中，漸漸的和e的主題有關了。由於金融貿易的需求增加，利息的複利計算變得非常的重要。其中，若將計息的次數趨近於無限大時，即是現今對e的定義：。理所當然的接下來，就是闡述極限的意義了。所以，第4章中，Maor開始說明何謂極限，如何計算極限。他舉了許多我們在高中課本中常看到的極限的例子，來說明一般情形下的極限取法。而又因為極限不定式的極限過程與一般基礎科學不同，不能依賴實驗數據而成為一個「定律」。所以，在此，Maor似乎要展現他的「博學多聞」，將焦點暫時轉移到數學與其他基礎科學的不同之處。之後，再將焦點繞回上。為了要將這個式子展開，需要二項式定理，接下來Maor先從巴斯卡三角形講起，再說明一下組合公式（這裡就顯得與主題無關了）。然後才是正題：將利用二項式定理展開。到此，Maor算是完整地說明e這個數字了。

        說明e這個數字的特性，必須藉助於微積分。所以，從第5章開始，Maor將注意力著重在微積分的發展上。他先要講「微積分的起源」，所以，他從阿基米德（Archimedes）開始，認為他的窮盡法已經相當接近現代積分學的想法了。他以阿基米德處理圓面積及拋物線為例，說明阿基米德的想法。最後Maor下了一個結論：「既然窮盡法相當接近現代的積分學，那麼為什麼當時希臘人沒有發明微積分呢？」（p.61）他的理由是：(1)因為希臘人認為無限是令人恐怖的事物（horror infiniti）。(2)因為希臘人沒有代數符號。為什麼覺得無限「恐怖」呢？當然必須從季諾（Zeno）的悖論（譯者翻譯成詭論）講起。第6章中，時間繼續往前微積分發現的推進，Maor提到了當時的環境背景：因為航海技術的需求，以及哥白尼天文學的影響，使得應用數學逐漸佔上風，而刻卜勒(kepler)的極微量方法(method of indivisible)就被Maor視為「離現代積分學只差一步」。（p.74）

        接下來，本書穿插一個第7章「求雙曲線下的面積」，再將e這個主題與積分結合在一起。從直線形面積公式的推導，到曲線下面積的求法需求而言，當然，就輪到笛卡兒與費馬的解析幾何出場了。所以，Maor敘述了笛卡兒的生平事蹟，他的座標幾何，及他的《幾何學》的影響。而費馬的故事中，就集中在他如何推導出的曲線下面積的積分公式，當然是個例外。而耶穌會教士聖文生（1584-1667），則推得曲線與x軸夾的區域面積應該是一個對數函數。接下來的，就交給微積分來處理了

        第8章中，以牛頓為主，Maor敘述了牛頓的生平事蹟、牛頓從巴斯卡三角形得到靈感的「無窮級數（infinite series）」，然後是牛頓的「流數法」。第9章的主角是萊布尼茲啦！同樣的，在這一章中，Maor敘述了萊布尼茲的微積分方法，同時，因為Maor要強調一個好的代數符號的便利，所以，他在處理萊布尼茲的方法時，就會著重在符號的運算上，並以實例來說明萊布尼茲的方法。在這一章的最後，不可免俗的，當然要提到微積分發明先後的爭論，以及這個爭論對英國及歐陸數學發展的影響。

        從第10章到第14章，主角又回到e本身了。有了微積分的襯托之後，就可以看出這個函數的特殊之處。第10章中，先說明的微分（變化率），以及在自然中的一些自然指數的例子，和解物理問題時會得到的一次及二次微分方程的解。再藉著指數與對數間互為反函數的關係，導出對數的微分。第11章是對數螺線的介紹。這時，當然必須介紹伯努力家族了。介紹了他們對數學的貢獻與成就，以及他們家人之間的互相爭吵之後，Maor將注意力轉回極座標與對數螺線的介紹。第12章處理了一個「懸著的鏈子」的問題之解決。這一條懸著的鏈子的圖形居然是這樣的曲線，而不是一般直覺認為的拋物線！而此時，當然就自然而然地引入的雙曲正弦（）等雙曲函數了。

        第13章說明這個函數的意義，當然主角就是歐拉（Euler）。在這一章中，Maor說明了歐拉的生平、他的一些數學成就，還有他對的定義及延伸，以及這個令人驚訝的式子。有了指數出現虛數的例子，當然就要進一步說明指數是複數的意義了。所以，在第14章中，Maor首先說明了「虛數」的誕生過程，負數與虛數的發展，到進一步的向量、複數平面的表示方式，最後就是的意義了。

        在後一章，當然要回歸到e到底是什麼的問題上。既然e是一個數字，當然要從數字的發展說起。從畢氏學派的自然數、有理數到無理數的發現，而後是戴德金（Dedekind）的分割，實數才算是完全有了嚴密的基礎了。但是，e只是一個無理數嗎？當然必須再進一步地區分成「代數數」與「超越數」。所以，結論是：e是一個超越數。（那超越數的「實質」意義是什麼？作者沒說！）

        Maor除了正文及附錄之外，在每一章的後面，都還會附上與正文相關的一些資料，或是補充數學算法上的不足，如對數的計算、極微量方法的使用；更有一些非常豐富的有關e的趣聞、歷史、及相關數學概念。像是自然界及藝術界中的對數螺線，讓人對大自然造物的奧妙，及人類藝術創作與數學結合的美嘆為觀止。這是Maor的書吸引人的一個特點之一。

        當我們看這樣一本科普書籍時，我們的期待是什麼？可能是知識的獲得。而從這一方面來看，Maor的這本書，算是達到了讀者的要求。他將有關e的概念發展，歷史典故，趣聞、以及應用，鉅細靡遺地呈獻給讀者。同時，他又減少了艱深的數學理論的推導過程，將整本書的數學門檻降低了許多，這也是他這一本書讓人覺得親切的地方。所以，我看完了這本書以後，總有參與了一次還算有趣的指數對數微分的教學活動之感覺。本書內容有很多是可以豐富我們教學活動的，除了相關數學家的生平之外，Maor引進的先求的導函數，再求它的反函數的導函數的方法，就是一個我實地應用的例子。同時，Maor提供的許多自然界及物理中有關自然指數函數的實例，也理應豐富了學生對e的瞭解。       

        但是，如果我們苛求一點，這一本書的許多地方是不合格的。當我們在看這樣一個數字的「歷史」時，不可避免的，一定會提到「人」的活動，而人的活動不應該只是有趣的軼事而已，社會的互動其實會影響到數學知識的發展方向，這一論點，現今的數學史研究或是數學教育研究都是贊同的，並且日漸受到重視。但是，在Maor的書中，我們看到的是數學知識的客觀性、普遍性，他對歷史的解讀，是一種「去脈絡」的方式，亦即將歷史事件以現今數學的眼光來衡量。雖然他想要以「歷史跳脫公式」，卻也只是將歷史當成是茶餘飯後，譁眾取寵的材料而已。

        例如，Maor提到了極限，也就是無限大或無限小的問題，他使用了將數「分割」，及「數學原子」這樣的字眼（p.40）同時，又提到了希臘人對無限的恐懼（p.63），為什麼會恐懼呢？希臘人對無限的恐懼影響的不只是當代人而已，其實一直到微積分的發明後，都還籠罩在它的影響下。這麼重要的一個文化脈絡，Maor卻是交代不清，或是隻字不提。Maor只有簡短的說明季諾悖論中的一個，想以這樣簡陋的說明打發讀者。熟悉希臘數學史或是科學史發展的讀者應該都知道，希臘人對於「變化」的興趣，以及當時兩派意見相佐的看法，一是認為運動是連續不可分的，以Heraclitus為代表；另一派認為時間或空間有最小的分割單位，以Democritus為代表。而Parmenides則兩者皆不同意，他認為運動是不可能的。他的弟子季諾就是為了要反駁這兩派的說法才提出那四個悖論。根據亞里斯多德流傳下來的記載，我們可以知道季諾的這四個悖論，前兩個是在反駁第一派的說法，後兩個是在反駁後一派的說法。因為季諾的「搗蛋」，及對變化問題的關切，卻又無法以理性說明清楚，所以希臘人不敢去碰觸這樣的問題。從此看來，阿基米德離積分的發現，不只是一步之遙而已，而是一條沒有辦法跨越的鴻溝。

        Maor在第15章中對畢氏學派的說法，也有一點是讓人啼笑皆非的。「發現這些洞（無理數）是畢達哥拉斯的功勞」（p.267）？這句話想必會讓畢格哥拉斯跳腳吧！他巴不得不要發現這些洞，這樣他的--「萬事萬物皆由自然數及其比值所構成」之主張才得以完整呀！無理數的發現著實困擾了畢氏學派許久，他們把這些數稱為「不可公度量的（incommensurable）」數，並不代表他們就欣然接受。同樣的問題也發生在刻卜勒身上，Maor說：「刻卜勒發現了五個正立體的幾何構造，他認為這些構造，決定了六個已知行星的軌道之間的差距」（p.71）。這句話有誘導讀者之嫌，刻卜勒最先在構思行星運行軌道的模型時，因為對柏拉圖的忠誠，所以才先以五個正立體為模型，在沒有辦法解決問題的情況下，才修正軌道成橢圓。（這點Maor在第15章時有提及，不過也只是一句話「誤入歧途超過三十年」而已。）

        同樣的問題也發生在「求的曲線下面積」及的誕生上。Maor在第7章「求雙曲線面積」這一章中，為了引進解析幾何，當然得提及笛卡兒及費馬。他說：「大約在十七世紀之初，好幾位數學家曾各自獨立地試圖解這個問題（即指介於的圖形、x軸及兩條垂直線及之間的區域面積），其中最有名的包括費馬及笛卡兒。」（p.82）雖然笛卡兒在1632年的書中，曾回答Mersenne有關的面積、體積和質量中心等問題，但在1637年他的《幾何學(Geometrie)》出版後，笛卡兒對這方面的問題的興趣已經減弱。[12]《幾何學》關注的焦點所在，是藉著代數的幫助，笛卡兒想以一個統一的方法，去解決幾何作圖的問題。[13]就我所看到的文獻而言，並沒有提及笛卡兒曾經去解過那個問題。Maor在這裡並沒有提供參考文獻，所以有點讓人無法信服。

        而在的誕生的故事中，Maor的看法就如同一般「不熟悉」數學史的教師們所認為的：誕生於解二次方程式中。Maor說：「方程式無解的這個問題，已經存在了好幾個世紀，……最早嘗試的人是義大利數學家卡丹諾，他在1545年試著找尋兩個數，使兩數和為10，而積為40。」（p.232）Maor沒有提及的是，卡丹諾這個問題出現在他於1545年出版的重要書籍《大法（Ars Magna）》的第37章中。而這本書的用意是在介紹三次、四次方程式的求根公式。事實上，卡丹諾在這本書的第十一章中，即給出解的方法。但是，同時他也碰到了「不可約」的三次方程式的問題，例如像是的不完全三次方程式，以卡丹諾解法，它的解為，但是我們又知道這個方程式有三個不同的實數解。卡丹諾沒有辦法處理這個問題，所以，雖然他在第三十七章中，看起來好像可以處理及這兩個數字，他卻也說「既精妙又無用（as subtile as it is useless）」。[14]的解的問題要到邦貝利（R. Bombelli 1526~1573）出版他的《代數學(L’Algebra opera)》中，才獲得解決，也才真正建立了虛數的運算法則。所以，這個數之所以變得不可忽視，是來自於解三次方程式中，而不是二次方程式。[15]

        上述所提及的，都是Maor在「應用」數學史時的一些「去脈絡」問題。當然，若公平一點的論斷，在一本科普的書籍中，要把歷史講得有趣，卻又得兼顧其歷史意義，並不是一件容易的事，或許我對Maor是有一點要求太過了吧！但是，有一點卻是我無法理解與諒解的，即是史料的錯讀。在本書的第5章「微積分的緣起」這一章中，阿基米德是一個很好的開端。在解釋阿基米德如何證明圓面積公式及如何求得π的近似值時，Maor說：「利用圓內接與外切正九十六邊形（他是從正六邊形開始，然後不斷把邊加倍）…」（p.59）而Maor所列出的參考文獻是Calinger編的 Classics of Mathematics，以及Heath 的The Works of Arichimedes。但是，在Classics of Mathematics中的阿基米德原文中，明明是從正四邊形開始，只是他把90度三等分，得30度，再將邊8等分，在一個360度的圓中，就得一正96邊形。這裡，就不曉得為什麼Maor會犯這樣的錯誤？實在讓人不解！

        最後，就是這一本書的翻譯問題了。這一本書由淡江大學數學系鄭惟厚教授翻譯，比起國內其他科普書籍的翻譯而言，他的翻譯算是問題很少的，只有幾個地方，可能也是很多科普書籍翻譯時常犯的錯誤：（1）method of exhaustion通常譯為窮盡法，或是窮竭法，而不是「窮舉法」（窮舉法類似歸謬證法，將所有的可能一一加以證明為誤，剩下的那一個即為真）。(2)在85頁中將Diophantus翻譯為狄歐范特斯，而在這一個的譯注說明中，卻又翻譯做丟番圖。(3)「incommensurable」通常翻譯做「不可公度量的」而不是「不可通約的」，「不可公度量的」這個詞有其歷史脈絡在。(4) 「Fermat’s Last Theorem」譯為「費馬最後定理」，而不是「費馬大定理」。(5) Maor這本書校稿時(1993)，懷爾斯確實才剛給出費馬最後定理的初次證明，但隨後被發現證明過程中漏洞，一直到1994年，懷爾斯才給出完整的證明。這一點譯者（尤其是一個常常翻譯科普書籍的譯者）似乎應該要知道，也應該在譯注中補充說明才是。[16]

        我這一篇書評，是從「略懂得數學史」的教師角度來批評的，所以，有些時候會顯得過於嚴苛。但是，若單就一般讀者，甚至是學校的數學教師而言，《毛起來說e》，不失為一本有趣、材料豐富，能夠讓教學活動更為活潑、生動的一本書。但是，若就一本書所背負的「教化」責任而言，它無疑是不合格的。畢竟，對以歷史來逃脫傳統數學知識中的冰冷、無聊的數學公式這一目標而言，「歷史」的解讀是很重要的。而「在脈絡」的解讀方式，對讀者在潛移默化當中的影響，亦是不能小覦。

附註：

[1]此處的新數學是指1960年代開始，美國因應科學教育改革所提倡的數學教學方法及內容。

[2] 此為Maor引用Edna Kramer的說法。

[3] 雷吉蒙塔努斯是米勒(J. Muller)的拉丁化名字。

[4] 常被譯作韋達，本文中有關名詞筆者儘量均沿用本書中文版的翻法，避免讀者閱讀上的困擾。

[5] 中文版將參考書目與圖片來源也當成附錄，所以共六個附錄。

[6] 希臘人主要關心的是球面三角形，至於平面三角學的發展，一直要到十六世紀。

[7] 見Victor J. Katz, A History of Mathematics, p. 461.

[8] 見Howard Eves, An Introduction to the History of Mathematics, pp.251-255

[9] 這提供一個數學社會史的例子。

[10] 德國的數學家凱斯特奈(Kastner)是第一位將三角函數定義成純數字，而非三角形的三邊長的比值。

[11] 已現代的符號來寫，就是圓內接四邊形ABCD中，對角線長乘積等於兩對邊長乘積的和，即AC．BD＝AB．CD﹢BC．DA。

[12] 請參考C. Boyer,  (1949)  The History of The Calculus and Its Conceptual Development. New York: Dover.
 P. 166.

[13] 參考Nuffield Foundation出版的The History of Mathematics. Singapore: Longman.

[14] 見於卡丹諾的Ars Magna, ff. 65v. 和 66r.，收錄於D. Smith, A Source Book in Mathematics.

[15] 請參考W. Dunham所著，《天才之旅》，台北：牛頓出版社。

[16] 請參考Simon Singhh著，《費馬最後定理》，商務出版社出版。