不一樣的組合數介紹
國立新店高中 蘇俊鴻老師
排列組合是研究一些基本的計數方法,對機率理論、系統分析、統計學及對局論等等,都是重要的基礎。在現行教材的安排上,不難看出教科書編者對組合概念的理解與教學上採用的策略是透過排列來學習,直接由排列數
![]() 引導出組合數
引導出組合數
![]() 的公式。這樣的論述安排有其便利性,但非介紹組合數的唯一途徑。清代的中算家汪萊(1768-1831)在他的算學著作《衡齋算學》第四冊後半的〈遞兼數理〉中,透過對物件選取配對的觀察,找尋規律性,進而配合堆垛求和的方法,提出組合數
的公式。這樣的論述安排有其便利性,但非介紹組合數的唯一途徑。清代的中算家汪萊(1768-1831)在他的算學著作《衡齋算學》第四冊後半的〈遞兼數理〉中,透過對物件選取配對的觀察,找尋規律性,進而配合堆垛求和的方法,提出組合數
![]() 的一般性公式,一起來看看汪萊是如何辦到的!
的一般性公式,一起來看看汪萊是如何辦到的!
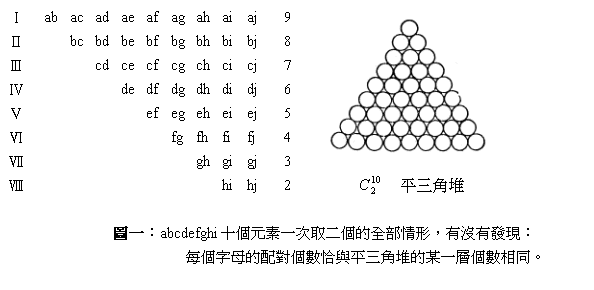
首先,汪萊透過觀察,發現平三角堆的總和與一次取出相異二物的組合數對應的規律性:
以一物為主而兼他物得若干數。至以又一物為主而兼他物即不復兼先為主之物,故所得必少一數。由此遞少遂成三角堆形。……以一物為主而兼他物得若干數,至以二物為主而兼他物,受兼之物已減為主之一,故所得必少一數,由此遞少故根數遞減。
由上文可知汪萊是利用選取的概念,先固定一物為主,考慮與他物逐一配對的所有情形,接下來先前之物便捨去不用,再另選一物固定,考慮與剩下之物配對的所有情形,以此規則類推下去。以
![]() 為例,考慮二物相兼的情形,作一說明。
為例,考慮二物相兼的情形,作一說明。
設有a,b、c、d、e、f、g、h、i、j等十個元素,依上述規則由a開始,因此與其他元素配對個數有九種,接著是b,由於a不算,因此與其他元素配對個數有八種,接著是c,……,組合的全部情形如圖一所示不難發現配對情形有九種(根數遞減),每一種情形的個數恰與九層的平三角堆的各層數目一一對應,因此汪萊利用三角堆來求和,顯得自然而然,水到渠成。
 |
一物為主而兼他物成一根,各物遞減而進成一平三角堆,至二物為主,則此物與彼物相與為二物,以兼他物成一根,此物與彼又一物又相與為二物,以兼他物又成一根,由此遞減而進,則一物為主已成平三角堆,各物遞減而進遂成立三角堆,由此遞進故乘數遞加。

汪萊的想法是先取二物(二物相兼)開始,其配對情形恰好與成一平三角堆相對應。再來考慮將平三角堆的每一層與第三物配對又可得出一平三角堆,最後再將其整合起來,恰與立三角堆的每一層數目一一對應。續以上例說明,寫出部份配對情形如下,請注意各層之配對情形,均由上例二物相兼情形擴展而得。不過第九層為ij,無法與其他物相兼成三物,故捨去。因此立三角堆的根數(層數)必須再減一為八。(如圖二)
事實上,我們由「十物遞兼分數圖解」可以看出,汪萊利用各種三角堆的和求出相對應的組合數
![]() :
:
以所設物數即為各立一數之數。減一數為三角堆之根,乃以根數求得平三角堆為二物相兼之數。又減一數求得立三角堆為三物相兼之數。又減一數求得三乘三角堆為四物相兼之數。如是根數遞減,乘數遞加,求得相兼諸數。……此遞兼之分數也。
配合汪萊所舉的「十物遞兼分數圖解」,此處我們以
![]() 為例說明上文,十件不同的物件中每次取一物的組合數就是物數10=
為例說明上文,十件不同的物件中每次取一物的組合數就是物數10=
![]() (“所設物數即為各立一數之數”)。十件不同的物件中每次取二物的組合數(“二物相兼”)等於一個九層(根數9=10-1)的平三角堆的總和(
(“所設物數即為各立一數之數”)。十件不同的物件中每次取二物的組合數(“二物相兼”)等於一個九層(根數9=10-1)的平三角堆的總和(
![]() )。十件不同的物件中每次取三物的組合數(“三物相兼”)等於一個八層(根數8=9-1)的立三角堆之和(
)。十件不同的物件中每次取三物的組合數(“三物相兼”)等於一個八層(根數8=9-1)的立三角堆之和(
![]() )。
)。

“如是根數遞減,乘數遞加,求得相兼諸數。”汪萊類推下去,一次取四件的組合數(“四物相兼”)就等於7層(根數為7=8-1)的三乘三角堆之和,一次取5件(“五物相兼”)的組合數就等於6層(根數為6=7-1)的四乘三角堆的總和,………。如此一來,便可由各對應的三角堆的總和將各種組合數(遞兼分數)
![]() ,
,
![]() ,……,
,……,
![]() 一一求出。再利用他在書中所給出的三角堆求積通法,我們就能得到
一一求出。再利用他在書中所給出的三角堆求積通法,我們就能得到
![]()
這與現在所學的組合數
![]() 計算公式一致。
計算公式一致。
汪萊將組合數定義成三角堆的和,使得組合與垛積術建立起關係,方法上是相當獨特的,在實際的教學中也是具體可行,帶給我們另一種體會組合概念的可能。此外在級數的教學中,我們也可以將汪萊的例子納入課外教材的補充,雖說汪萊所用的三角堆求和是屬於階差級數的範疇,但並不難理解。對於級數與其他數學領域的結合,提供一個良好的範例。由此也不難發現在豐富教材內容上,古代文本可以提供教學上更多的揮灑空間,這也是HPM努力的目標之一。