三角函數公式的托勒密方法

西松高中 蘇惠玉老師

托勒密的生平所知不多，較為著名的是他的許多重要著作。例如，在他的《地理學（Geography）》中所繪製的地圖中，畫出了經緯線，同時，討論了製作地圖所需的透射學的技巧。他還寫過有關天文、音樂和光學的著作和試著去證明歐基理得的平行公設。他最著名的書為Mathematical Collection，全書共十三冊，完整的包含了當時希臘人對宇宙的模型和描述，如同《幾何原本》一般，他將之前所有的成果收集在這一本書中，可以說是希臘天文學的集大成，在十六世紀哥白尼的學說被廣為接受之前，是最有影響力的天文學作品。幾世紀之後的阿拉伯稱此書為al-magisti，意即the greatest，以區分其他內容較少的天文作品。從此，這本書就被稱為The Almagest。

在托勒密的The Almagest的第一冊中，記載了托勒密如何做出他的弦表，給出圓心角及其相對應的弦長。托勒密為了要製作他的弦表，證明了一連串的幾何命題，從他對正弦的定義（圓心角所對的弦長），或是餘弦的定義（圓心角之補角所對之弦長，他稱之為半圓的剩餘，remainder of the semicircle），可以得到現今所謂的和角、差角、半角公式，其中，以托勒密定理（圓內接四邊形對角線的乘積等於對邊的乘積和）作為證明的工具。

托勒密定理

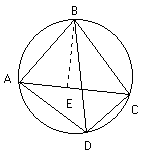
有一圓及圓內接任意四邊形ABCD，連接AC及BD。證明

矩形 AC,BD=矩形 AB,DC+矩形 AD,BC.

作角ABE，使得角ABE=角DBC
加上共同的角EBD後，角ABD=角EBC
但是，角BDA=角BCE [Eucl. III, 21]，因為他們對同一弧。所以三角形ABD與三角形BCE相似，所以
BC：CE :: ¹BD：AD [Eucl. VI, 4]
所以，矩形 BC,AD=矩形 BD,CE
同時，因為角ABE=角CBD，且角BAE=角BDC，所以三角形ABE與三角形BCD相似，所以
AB：AE :: BD：CD
所以，矩形 AB,CD=矩形 BD,AE，
且因為 矩形 BC,AD=矩形 BD,AE
所以，矩形 AC,BD=矩形 AB,CD+矩形 BC+AD [Eucl. II, 1]

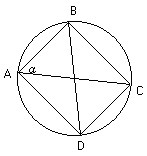
        此即為有名的「托勒密定理」：任意圓內接四邊形中，對角線的乘積=兩雙對邊的乘積和。在這個定理中，若將圓內接四邊形特殊化成圓內接長方形，對角線AC為直徑=1時，若 ，則可以輕易的得到 這個重要公式。

差角公式：

半圓形ABCD，AD為直徑，從A點畫兩條弦AB、AC，給定這兩條弦的長度，以直徑120來表示；連BC。則BC可求。

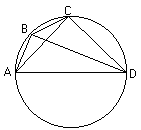連接BD，CD。則很明顯的，他們的長度可知，因為他們為半圓的剩餘（remainder of the semicircle）所對的弦。²因為四邊形ABCD為圓內接四邊形，所以，
矩形 AB,CD+矩形 AD,BC=矩形 AC,BD
因為矩形AC,BD已知，且矩形AB,CD已知，所以，剩下的矩形AD,BD可知。
且AD為直徑，所以BC可求得。

        托勒密這個命題的意義，在於給定兩個角度及其所對的弦長，可以求得兩角度之差所對的弦長。這個命題，即是我們常看到的差角公式： 。若AD為直徑=1， ，則BC=sin(α-β)，且BD=sinα，AB=cosα，CD=sinβ，AC=cosβ。由上述的「托勒密定理」，即可得到 。

半角公式：

設ABC為半圓，AC為直徑。給定弦長CB，D平分此弧。連AB，AD，BD及DC。從D作DF垂直AC。則，CF=1/2(AC-AB)。

作AE=AB，連接DB。因為AB=AE，且AD為公共邊，且角BAD=角EAD[Eucl. III, 27]，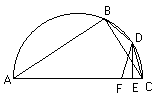
所以，底邊BD=底邊DE[Eucl. I, 4]
但是，弦BD=弦CD，所以，弦CD=DE。
因為在等腰三角形DEC中，DF為從頂點到底邊的垂直線，
所以，EF=CF [Eucl. I. 26]。但是，
CE=（AC-AB），
所以，CF=1/2(AC-AB)。
所以，因為弦BC已知，所以，半圓的剩餘所對的弦AB亦可知。所以CF=1/2(AC-AB)也可知。但是，因為DF畫在直角三角形ACD中，所以直角三角形ACD相似於直角三角形DCF[Eucl. VI, 8]，所以，AC：CD :: CD：CF。即矩形 AC,CF=正方形 CD。但是矩形AC,CF已知，所以CD上的正方形可知，所以，弧BC的一半所對的弦CD的長度可知。

        托勒密證明完這個命題後，說明了如何得到一半角度所對的弦長。即若直徑AC=1， ，則BC=sinα，AB=cosα，從上述的命題知道CF=1/2(AC-AB)=1/2(1- cosα)。但是，直角三角形ACD與直角三角形DCF相似，所以， ，即 。

和角公式：

有一圓ABCD，直徑為AD，F為圓心。從A連續的切出兩弧AB、AC，連接AB、AC。給定此相對的兩弦AB、AC的長度。連接AC。則AC可得。

過B點畫圓的另一條直徑BFE，連BD、DC、CE和DE。由此，很清楚地，因為BC已知，所以CE可知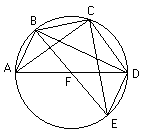。且因為AB已知，所以BD和DE可得。由我們所已經證明的，因為BCDE為圓內接四邊形，BD、CE為其對角線，對角線所組成的矩形等於由對邊所組成的矩形和。所以，因為矩形BD,CE和BC,DE可知，所以，矩形BE,CD可得。但是，BE亦為直徑，所以剩下的CD可得。所以，半圓剩餘所對的弦AC可得。如此，如果給定兩角度及其所對的弦，由這定理可知，這兩個角度的和所對的弦亦可得知。

托勒密的這個命題，從兩已知角度所對應的弦長，求得兩角度之和所對應的弦長，即是我們所謂的和角公式： 。若直徑BE=AD=1， ，則BD=cosα，CE=cosβ，BC=sinβ，DE=sinα，所以，而由「托勒密定理」知，BD×CE=CD×BE+BC×DE，即 ，所以，
CD=cos(α+β)= 。而AC=sin(α+β)亦可求得。

附註：我們可以從托勒密的方法得到正弦定理及餘弦定理的證明，簡單易懂，可以當作教學上的參考。

正弦定理：

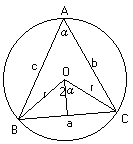一圓半徑為r，圓心為O，圓內接三角形ABC中，設α為銳角，則

，自O做BC邊的中垂線，則 ，所以，

。同理 。

餘弦定理：

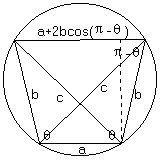如圖，ABCD為圓內接梯形，由托勒密定理可知：

c×c=b×b+(a+2bcos(π-θ))×a，即

。[由Sidney H. Kung所給出]

[1] 在希臘時期，無法直接將a: b看成是一個數 ，他們將比例相等看成是一種「類比」，以「::」來表示。

2 此為托勒密對餘弦函數的定義。

參考文獻

Ptolemy, C. (c. 100-178 C. E.), The Almagest, in Greek Mathematics Volume II: From Aristarchus to Pappus, with an English translation by Ivor Thomas.Cambridge: Harvard University Press.

Ptolemy, C. (c. 100-178 C. E.), The Almagest, in Great Books of The Western World Volume 15, translated by R. Catesby Taliaferro. Chicago: Encyclopaedia Britannica, INC.

Euclid (1956), The Thirteen Books of The Elements, translated with introduction and commentary by Sir Thomas Heath, New York: Dover.

Katz, V. (1993), A History of Mathematics: An Introduction. New York: HarperCollins College Publishers.

Nelson, R. B. (1993), Proofs Without Words—Exercises in Visual Thinking. Washington DC: MAA.

Maor, E. (1998)，《毛起來說三角》（胡守仁中譯）。台北：天下文化。