幾何『修辭』：笛卡兒 vs. 歐幾里得

台師大數學研究所碩士班研究生 黃清揚

摘譯序

    本篇文章摘譯自1988年二月出版的雜誌For the Learning of Mathematics

中John Fauvel的著作 “Cartesian and Euclidean Rhetoric” (pp. 25-29)。這裡要對『修辭』做個解釋，這一名詞在此特別是指數學文本中的書寫方式，包含語調（法）及文字的使用。而書寫方式的不同就好比不同老師所採用的不同上課方式，有沉悶也有愉悅。作者基於對數學教育的關懷，整合數學史的發展寫下了這篇文章，並給大家深刻的省思。

前言

在日常教學環境中，是否有一種最好的方式來溝通數學？以時間至上的上課模式來說，學習者日復一日的坐在椅子上，看著教師在黑板上書寫的背影，每次五十分鐘，並接受一連串像是輔助定理、定理4.2.1、證明以及備註等等數學知識。這種方式對講課者來說是方便的，學生也易於記憶，缺點則是學生無法察覺數學是可親近的，甚至從開頭便不知所措，失去學習的樂趣。另一種講課方式，老師能激發學生的熱情，引導學生相信數學是一門真正有趣的科目並樂意學習。這種方式雖然留給學生溫暖與快樂的感覺，但是，它的缺點則是未給予學生充分的實質內容來強化這種感覺，或是讓學生誤以為這門課是簡易的，但在自行研讀時，遭遇到極大的困難。

以上所述，也見於各種數學的文本。於此，這裡便是要介紹過去兩種有著高度影響力的著作：300B.C.左右歐幾里得所著的《幾何原本》(The Elements) 與笛卡兒1637年出版的《幾何學》（Geometry）。文章中我將數學的溝通描述為毆幾里得或是笛卡兒『修辭』是根據某一個文本讀起來與看起來比較像《幾何原本》或《幾何學》而定。再說到『修辭』與數學的連結，這裡僅止於關懷語言如何用於溝通數學，一位作者選擇怎樣的寫作方式與來讀者溝通，所呈現出來的『修辭』正是本文關注的焦點。

歐幾里得『修辭』

    《幾何原本》中『定義-公理-命題-證明』的型式是歐幾里得對上千個相似的產品最終的巧思。我們評估歐幾里得『修辭』，特別有趣的地方是他完全直接的態度：沒有跡象顯示作者曾經注意到讀者的存在，因為在書中他努力地在陳述所謂「永恆的真理」。這種模式已被證明為高度成功的書寫方式，明顯地，故意忽略讀者一直不被視為是不容易理解的。

笛卡兒「修辭」

    笛卡兒的《幾何學》提供讀者另一種『作者與讀者』關係的世界。《幾何學》乃是1637年於萊登（Leiden）出版的《方法論》（Discourse on method）中附於書末三篇論文中之最後一篇。《方法論》中所採用的口吻與《幾何學》是一致的，笛卡兒告訴讀者他提供這本書僅當作是歷史或是虛構的故事。而書中對不同時間的描述有著精細的控制，譬如它包含了『寫作的時間』、『讀者經由文本進展的時間』以及『描述事件的時間』等等。簡而言之，笛卡兒絞盡腦汁來定義及架構讀者的反響，而這也是最成功的策略。

    檢視《幾何學》，笛卡兒將所訴求的讀者對象設定在『初學者』，因為他在開宗明義就指出：

到目前為止我已經試著讓每一個人對我的意思能清楚的了解；但我懷疑是否這篇論文能被不熟悉幾何的讀者來閱讀，因為我已經認為重複在裡面的論述是多餘的。

相較之下，《方法論》中其他的部分則並非如此。我們要特別注意到《幾何學》反而是放在《方法論》最後的地方。由此看來，儘管他使用的是家鄉話以及較愉悅的模式，作者似乎在前提上就認定大多數的讀者不能讀懂他的書。對於當時的同行來說，他的書的確與眾不同，也因為他的書難以了解，我們也可想像笛卡兒如何技巧性的贏得聲名與喝采。

    在書寫方式上，笛卡兒用的是友善及直接訴求般迷人的語調，這種語調不像出自數學家反倒像是一位工匠告訴讀者如何製作傢俱：

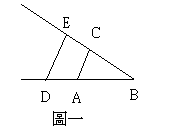
      假定AB是單位，現在想要將BC乘BD，我只要連接點A與C，然後畫CA的平行線DE，BE即為乘積。（如圖一）

相較於笛卡兒，歐幾里得則採用面積來操作（因為對歐幾里得來說，兩個數或量相乘其結果必須用面積來替代，並且數與量要分開處理），其語調就較為嚴肅，請參見《幾何原本》第七冊定義16：

兩數相乘得出的數稱為面，其兩邊就是相乘的兩數。

有了以上定義之後，接下去他才處理數與量的乘法。

另外，對於讀者來說，笛卡兒體貼地未將數學知識所有細節陳述出來（歐幾里得則否），因為他認為過多的敘述令人感到厭煩，如果將這些刪掉的部份留給讀者自己來發現，或許他們會覺得更有樂趣才是。

最後，笛卡兒相信用這樣的『修辭』方式來縱貫全文，後人會給他仁慈的評斷，事實的確也是如此。

笛卡兒『修辭』的成功

    雖然笛卡兒最初的文本曾讓讀者稍稍懷疑他的才華，但經由荷蘭籍拉丁文譯者Frans van Schooten的努力，卻使它在數學社群中博得好評，並風靡到法國以外的地區。如同Jan van Maanen曾經指出：笛卡兒的數學能夠普及，大部分的成就要歸功於Frans van Schooten，並經由此一荷蘭人，《幾何學》成為教育性的文本。

修辭學上的回嚮

    綜觀數學史，歐幾里得與笛卡兒『修辭』絕不是數學文本中僅有的兩種書寫方法（英國數學家Robert Record另有一種柏拉圖式的『修辭』風格）。我們在檢視其他人的『修辭』時，也必須面對自己的實務經驗。為了不同的目的（教師或作者），我們應該使用怎樣的「修辭」呢？而這種形式的「修辭」在溝通上又是如何進行？（特別是在課堂上教師如何與學生溝通？）從HPM的觀點來看，企圖回答這些問題，一定可以幫助我們從自身實務經驗跳脫出來，賦予批判性的反思，並且擴及其他可能的領域之學習。