如何利用古代數學文本作為認知的媒介？

                                                                                                   台師大學數學系 洪萬生教授

        對於如何活用古代數學文本到教學之中，荷蘭HPM學者Barbara Van Amerom引述了她與 Leen Streefland合寫的一篇論文，其中利用了中國漢代《九章算術》『方程章』中的第八題，來說明『以物易物脈絡』(barter context) 如何地可以協助學生「發展出 （前）代數 ((pre-)algebra) 的記號與工具，比如對於基本運算與其逆運算的一個良好理解、對於字母與符號在不同情鏡中的意義之開放態度，乃至於推論已知或未知數量的能力。」茲先轉述此一題問、『答曰』與『術曰』如下：

今有賣牛二、羊五，以買一十三豕，有餘錢一千；賣牛三、豕三，以買九羊，錢適足；賣六羊、八豕，以買五牛，錢不足六百。問牛、羊、豕價各幾何？

        答曰：牛價一千二百，羊價五百，豕價三百。

        術曰：如方程。置牛二、羊五正，豕一十三負，餘錢數正；次，牛三正、羊九負，豕三正；次，五牛負、六羊正，八豕正，
   不足錢負。以正負術入之。

現在，將上述解法翻譯成現代形式。如設b、w、p分別代表牛、羊、豕之價錢，則利用『方程術』，我們可以將它轉換成為寫出如下聯立方程組：

             2b + 5w – 13p = 1000

                3b – 9w + 3p = 0

                -5b + 6w + 8p = -600

為了利用此古典一文本，Van Amerom與 Streefland將上述方程組改寫成如下形式：

                2b + 5w = 13p + 1000      (1)

                3b +3p = 9w              (2)

                6w + 8p + 600 = 5b       (3)

他們顯然是為了在此一從算術過渡到代數的階段中，避開負數及其加減法則。而後者正是《九章算術》『正負術』之精華所在。不過，更重要的，是他們相當敏銳地注意到上述方程式(2)中的『以物易物』之意義解讀。其中，由於不涉及錢數，所以，b、w、p也可以表徵動物本身。至於方程式(1)、(3)所引進的錢數的結果，則不止因而改變了方程式的媒介 (medium of the equation) -- 從『動物數』到『錢數』，同時，也改變了未知數 (unknowns) 的意義 -- 從『實體相關』(object-related) 到『實體性質相關』(quality-of-object-related)。

        接著，或許大家也有興趣瞭解《九章算術》作者（不詳）如何利用所謂的『方程術』來解此一聯立方程組。請先欣賞郭書春針對本題的現代白話文翻譯：

假設賣了2頭牛、5隻羊，用來買13隻豬，還有餘1000錢；賣了3頭牛、3隻豬，用來買9隻羊，錢恰好足夠；賣了6隻羊、8隻豬，用來買5頭牛，不足600錢。問1頭牛、1隻羊、一隻豬的價錢各是多少？

    答：1頭牛的價錢是1200錢，

1 隻羊的價錢是500錢，

1 隻豬的價錢是300錢。

術：如方程那樣求解。佈置牛的頭數2、羊的隻數5、正的，豬的隻數13，負的，餘錢數，正的。接著，佈置牛頭數3，正的，羊的隻數9，負的，豬的隻數3，正的。再佈置牛的頭數5，負的，羊的隻數6，正的，豬的隻數8，正的，不足的錢數，負的。將正負術納入之。

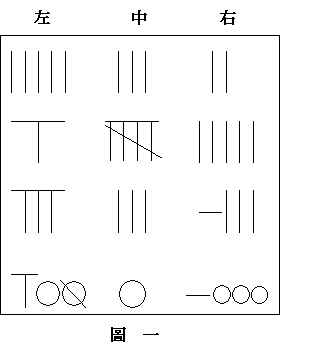
按照中國古代籌算圖示，此一聯立方程組可以運用算籌佈置成下列圖一形式。如果我們將它逆時針旋轉改寫成現代（矩陣）形式，則有如圖二。再運用『方程術』（近於增廣矩陣的『高斯消去法』或『列運算法』），則可以變換成圖三形式，於是得出一個同義方程組如下：

                2b + 5w - 13p = 1000

                      11w – 15p = 1000

                                  8p = 2400

如此一來，就可以求得答案了。

        至於所謂的『方程』，按照魏晉劉徽的《九章算術》注文：「程，課程也。群物總雜，各列有數，總言其實。令每行為率，二物者再程，三物者三程皆如物數程之，并列為行，故謂之方程。」再對照郭書春的白話文翻譯：「程，就是求解其標準。各物品混雜在一起，各列的數值都有差別，總的表示出它們的實。使每行作為率。兩個物品的情形有二程，三個物品的情形有三品，程的的多少都與物品的種數一致。把各列並列起來，就成為行，所以叫做方程。」我們多少可以瞭解這是『聯立方程組』(system of equations) 的意思。不過，難免有如劉徽所指出的『空言難曉』，所以，他特別舉例說明。事實上，針對本章第一題，劉徽的註解非常詳盡，依據它我們很容易還原中國古代的『方程術』，而且也可以確定：此『術』與矩陣理論中的列運算法，的確十分神似。不過，這些都無關國中數學教學，我們就不多說了。

                     2　　5　　-13　　1000

                     3　　-9　　3　　　0

                     -5　　6　　8 　　-600

圖　二

                      2　　5　　-13　　1000

                      0　　-1　 -15　 　1000

                      0　　0　　 8   　2400

圖　三

參考文獻

Fauvel, John and Jan van Maanen eds. (2000). History in Mathematics Education: An ICMI Study. Dordrecht / Boston / London: Kluwer Academic Publishers.  

Streeland, Leen and Barbara A. van Amerom (1996). “”Didactical Phenomenology of Equations”, in Gimenez, J., Campos Lins & B. Gomez eds. Arithmetics and algebra education: Searching for the future (Taaarragona: Computer Enginiering Department, University Rovira I Virgile), pp.. 120-131. .

Van Amerom, Barbara A. (2002). Reinvention of Early Algebra: Developmental research on the transition from arithmetic to algebra. Ph.D. dissertation thesis. Utrecht: Frendenthal Instituut. 

Van Maanen, Jan (2001). “Research on History in Mathematics Education in the Netherlands: The ‘Reinvention Studies’”, presented to The Netherlands and Taiwan Conference on common Sense in Mathematics, November 19-23, 2001, National Taiwan Normal University, Taipei, Taiwan,

HPM台灣網頁：http:/math.ntnu.edu.tw/~horng。

郭書春譯注 (1998).《九章算術》，瀋陽：遼寧教育出版社。

郭書春、劉鈍校點 (1998).《算經十書》，瀋陽：遼寧教育出版社。