從幾何面向看

西松高中 蘇惠玉老師

一、前言

在《HPM通訊》第四卷第七期中，黃哲男再他的文章〈 〉中，告訴我們一個令人驚訝的觀察結果。在看到他的文章之前，我從來沒想過 和A4、B4的紙張大小有關。如果從A4，A3的邊長來看，

A4紙張的大小：210×297mm， ＝1.414285714…

A3紙張的大小：297×420mm， ＝1.414141414…

A4、A3的長與寬的比大約是 ，為什麼會有這麼奇妙的結果？黃哲男猜測是，要使一個長方形，分成兩等分後，小的長方形與原長方形相似，那麼小長方形的邊長比為當然必須為 ！

      ＝

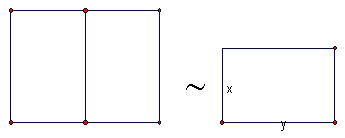
耶？ ＝ ？ 不是無理數嗎？所謂無理數不是不能寫成分數的形式嗎？為什麼會和「邊長比」有關係？我認為這一點當成教學上的切入點，可能會有不同的趣味產生。以下我試著從幾何的角度來看「 是無理數」這個數學概念，從無理數的幾何意義，到「 是無理數」的幾何證法，最後是 的幾何逼近方法。試著從幾何面向來看 ，以補充課本從代數面向來看的不足。

二、The Meno

   柏拉圖的數學哲學論述，主要發表在他的著作《米諾》(The Meno) 之中。在本書中，對話的人物共有四位，即蘇格拉底、米諾、Anytus 與米諾家的一位（奴隸）男孩 (slave boy)。柏拉圖藉由蘇格拉底「引導」奴隸男孩如何得到一個新的正方形，面積是原有正方形的兩倍的對話，來闡述他的數學哲學：即每個人心靈中出生時就帶有數學知識，只要經過適當的「引導」，就可以喚醒這些記憶。所以，數學教育是一種「再發現」的過程。

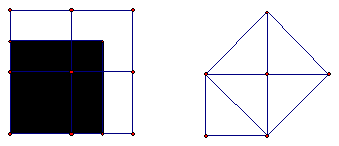        為了要得到兩倍的正方形面積，奴隸男孩先是將邊長增加為兩倍，面積成了四倍；然後奴隸男孩將邊長增加成 倍，結果面積變成兩倍多一點，最後，蘇格拉底「引導」奴隸男孩「考慮」以原正方形的對角線為邊長，所得到的新正方形。從這裡，可以引申為 ，換句話說， 。¹ 這一個「數字」，到底與邊長、對角線等「幾何量」有何關係？

三、            可公度量的與不可公度量的

如果我們從有理數的英文rational number來看，rational一般的理解都是「有道理的」，那麼，應該是什麼道理？從ration的拉丁文語源來看，rational 是從ratio 演化而言，原意是「比」的意思；亦即可以寫成兩個整數之比的，叫做有理數。那麼，無理數呢？irrational number，自然就是不能寫成兩個整數之比的數。這個概念及形式，是從畢氏學派的「可公度量的」與「不可公度量的」觀念演化而來的。

  畢氏學派 (Pythagoreans)是指畢達哥拉斯（大約西元前572-497）和他的門徒們，這個帶有神秘主義與宗教色彩的學派，相信「數目 (number) 是所有事物的本質」，這裡的「數目」指的是正整數。畢氏學派相信的，不只是所有物體都有數，或者是這些物體能被排序、被量化，他們更相信數目是所有物理現象的基礎。例如，行星的運行可已以數目之間的比來表示；音階也可以數目比的形式展現，還有直角三角形的邊長比等等。對畢氏學派而言，數目永遠和事物的計算連在一起，而計算就必須要有不可分割且保持不變的單位元存在。而為了計算「長度」，當然就需要有度量單位，畢氏學派假設認為永遠都可以發現這樣一個度量的基本單位，而一旦這樣的單位被找到了以後，它就成了不可分割的單位元了。兩個線段長如果都可以用同一個單位元量盡，就稱這兩個線段長為「可公度量的」(commensurable)，如右圖的 與 ；反之，如果不能同時量盡，就稱「不可公度量的」(incommensurable)，如正方形的邊長與對角線。這裡，畢氏學派的錯誤在於他們無法確認「數」與「幾何量」的分別，「數」的單位元是不可分割沒錯，但是「幾何量」是可以「無窮盡地」的分割的。

        雖然畢氏學派無可避免的一定會碰到「不可公度量」的數，他們也了解「可公度量」與「不可公度量」之間的不同，但是，為了保持學派理論的完整性，他們選擇保守秘密。如今，我們可以在亞里斯多德的書中看到一點點「不可公度量」的數存在與被證明的蛛絲馬跡，證明形式即是現今證明「 是無理數」的證法。而數學史家Heath認為，這也是畢氏學派證明 的不可公度量性的證明方法。亞里斯多德引用這個證明當例子，來說明他的「歸謬證法」(reductio ad absurdum)：如果正方形的邊長和長是可公度量的，那麼，就會得到有一個數同時是奇數也同時是偶數 (on the assumption that the diagonal of a square is commensurable with its side, it is proved that odd numbers are equal to even)。其證法如下：

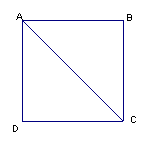若AC為正方形ABCD的對角線，其邊長為AB，

假設AC與AB是可公度量的，

設α：β是他們的最小正整數比，

則α>β>1，而

AC²：AB²＝α²：β²，而因為AC²＝2AB²，所以α²＝2β²

所以α²為一偶數，故α為一偶數；

因為α：β是最小的正整數比，所以β必須為一奇數。

設α＝2γ，所以4γ²＝2β²，β²＝2γ²，

所以β²為一偶數，故β為一偶數，這是不可能的。

這個證法曾經被竄改成歐幾里得所寫，而誤植成《幾何原本》的第十卷第117個命題，但在李善藍與偉烈亞力和譯的《幾何原本》後九卷(1857)中，仍存在此一命題：「凡正方形之邊與對角線無等」。²同時，李善蘭還在此命題的「案」中，將線段的不可公度量，擴充到面積與體積的不可公度量。這是中國數學史上第一次討論不可公度量，即無理數的問題。如此看來，當初的誤植，也許啟發了無數後人研究無理數，或是數學的熱情與眼光，而這又是另一個故事了。

四、 幾何證法

上述的證明，雖然與現今證明「 是無理數」的證明無異，但是是從「可公度量」的意義出發，來證明「不可公度量」，不像現今，完全是代數符號的操弄。要證明「 是無理數」，亦即證明正方形的邊長與對角線是不可公度量的，還可以從純粹幾何的角度來證明，畢竟，無理數的「不可公度量性」就是從幾何量的度量產生，它的定義，本身就有很強烈的幾何意涵。而證明的基本形式，在歐幾里得的《幾何原本》(The Elements) 中即可找到。

歐幾里得《幾何原本》第七卷第1個命題寫道：

設有不相等的二數，從大數中連續減去小數直到餘數小於小數，再從小數中連續減去餘數直到小於餘數，這樣一直作下去，若餘數總是量不盡其前一個數，直到最後的餘數為一個單位，則該二數互質。(Two unequal numbers being set out, and the less being continually subtracted in turn from the greater, if the number which is left never measures the one before it until an unit is left, the original numbers will be prime to one another.)

這個命題即是所謂的轉轉相除法。這個命題是「數」的形式，藉由亞里斯多德的看法：當量盡前一個量的更小的量無法被找到時，這個過程將會『無法確定地』（indefinitely）繼續下去。歐幾里得在第十卷第2個命題中，將「數」的形式，引伸到「量」的形式：

如果從兩不等量的大量中連續減去小量，直到餘量小於小量，再從小量中連續減去餘量直到小於餘量，如此一直作下去，當所餘的量永遠不能量盡它前面的量時，則兩量不可公度。(If, when the less of two unequal magnitudes is continually subtracted in turn from the greater, that which is left never measures the one before it, the magnitudes will be incommensurable.)

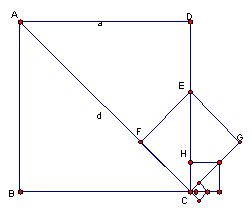
我們可以從命題2得到 的不可公度量性證法。如下圖：d, a分別是正方形ABCD的對角線長與邊長，從對角線AC中減去邊長CD的長度AF，再從CD中減去CF的長度得到CE，再從CE中減去CF得到CH，再從CG(＝CF)中減去CH，…如此進行下去，由於對角線與邊長絕不相等，所以我們可以繼續「無窮盡」的作下去，由命題2，我們可知，正方形的對角線與邊長是不可公度量的。

五、  的有理逼近

是一個無理數，那 到底是多少？以下是Theon of Smyrna（西元第2世紀）所給的一個 的有理數逼近的方法。這個方法要從《幾何原本》的第二卷命題10說起：

如果二等分一條線段，且在同一直線上再給原線段添加上一條直線，則合成線段上的正方形與添加線段上的正方形的和等於原線段一半上的正方形與一半家上添加線段之和的正方形的和的二倍。

如圖，即AD²+DB²=2(AC²+CD²)

若AC＝小正方形的邊，BD＝對角線，則BD²＝2AC²，

所以，AD²＝2CD²

設AD＝大正方形的對角線，CD＝大正方形的邊，設AC＝s，BD＝d，則可得到

CD＝s＋d，AD＝2s＋d

在西元第2世紀時，Theon of Smyrna以如命題10的形式，用畢氏學派的說法，造了兩個數列，Theon以1 (unit)當成第一個數，然後，

“Now there are added to the side a diagonal and to the diagonal two sides…”

令s₁＝d₁＝1，

對所有的自然數n，令s_n+1＝s_n+d_n ，d_n+1＝2s_n+d_n，則

我們可以用數學歸納法證明 ，亦即 ，即這兩個數列的比值趨近於 。如果我們以圖形來表示，令D_n為以s_n為邊長的正方形的對角線，我們可以發現，畫到第三個數時，D₃與d₃幾乎不能區別，亦即比值已經很靠近 了。

註解：

1. 對柏拉圖而言，正方形對角線與邊長是不可公度量的，即 與1的不可公度量是不需要懷疑的。因為他在《Theaetetus》中，告訴我們Theodorus of Cyrene證明 …一直到 與1是不可公度量的，他略過 ，可能對他而言， 與1的不可公度量是已知的。（請參考Heath在《幾何原本》第十卷前的引言）

2. 在E. F. August(1826-9)與Heiberg(1883-1888)的版本中，此命題已移至附錄。但在李善蘭與偉烈亞力合譯的《幾何原本》後九卷（第七至第十五卷）中，其中第十卷仍包含第117命題。據考證，他們所翻譯用的底本，可能是參考I. Barrow的版本，該版本在1655年以拉丁文出版，直到1732年仍有許多版本，其中有一些是英文翻譯本。

參考文獻：

Daumas D. and M. Guillemot (1997). ‘Must we always be rational? From incommensurable magnitudes to real number’, in Evelyn Barbin ed., History of Mathematics—History of Problems (translated by C. Weeks). Paris: ellipses.

Euclid (1956). The Thirteen Books of The Elements (translated with introduction and commentary by Sir T. L. Heath). New York: Dover Publications, INC.

Heath, Thomas L. (1949). Mathematics in Aristotle. Oxford: Clarendon Press.

Katz, V. J. (1993), A History of Mathematics, New York: HarperCollins College Publishers.

李善蘭、偉烈亞力合譯 (1857)，《幾何原本》後九卷，收錄於《中國科學技術典籍通彙》數學卷五，河南教育出版社。

王渝生 (1993)，〈幾何原本提要〉，收錄於《中國科學技術典籍通彙》數學卷五，河南教育出版社。

洪萬生 (1999)，〈閒話 〉，收錄於《孔子與數學—一個人文的懷想》，台北：明文書局。

黃哲男 (2001)，〈 〉，《HPM通訊》第四卷第七期。