魅力無窮的『祖率』：
台師大數學系 洪萬生教授
一、前言
所謂『祖率』，是指中國南北朝時期祖沖之
(427-500) 所推算出來的圓周率近似值：355/113。它是日本數學史家三上義夫
(Yoshio Mikami) 建議使用的稱呼，顯然他是用來推崇祖沖之在這一方面的偉大貢獻。從數學知識本身來看，此一近似值當然有它的過人之處或獨特之美，否則就不須要如此大費周章了。
問題是：『祖沖之知道圓周率
是常數或定值嗎？』乍看之下，這個問題簡直是廢話！如果不知道的話，那麼，圓周率『近似值』這個名詞有意義嗎？還有，這一篇文章還需要撰寫嗎？
其實，根據《隋書．律曆志》的記載，祖沖之當然知道圓周率是一個常數！而且，他也正是據此所作的近似值追求，而成就了數學史上的不朽聲名。
熟悉歷史的人，難免都喜歡引經據典！現在，且讓我們一起來看看《隋書》《律曆志。備數》怎麼介紹『祖率』：
圓周率三，圓徑率一，其術疏舛。自劉歆、張衡、劉徽、王蕃、皮延宗之徒，各設新率，未臻折衷。宋末南徐州從事史祖沖之更開密法，以圓徑一億為一丈，圓周數盈數三丈一尺四寸一分五釐九毫二秒七忽，朒數三丈一尺四寸一分五釐九毫二秒六忽，正數在盈朒二限之間。密率：圓徑一百一十三，圓周三百五十五；約率：圓徑七，圓周二十二。
解讀這個文本，最好同時具備『歷史』與『數學』的起碼素養。譬如，我們對於劉歆等人物、乃至於祖沖之的官銜『宋末南徐州從事史』的認識，主要來自一般歷史，至於如何理解上述這些數目字的意義，那就非得懂一點數學不可了。當然，如果想要考察劉徽與祖沖之兩人數學研究之間的關聯（請注意一般的歷史論述無從找起），那麼，『數學史』的素養，就變得不可或缺了。
二、一個教學的插曲
既然說到數學史，我這個專業的數學史家就不免技癢－『老王賣瓜』。最近，我在本系『數學史』教學中，將它設計成為一個課後作業（參考附錄I），請選修本系『數學史』課程的學生來回答下列問題：
請問祖沖之的圓周率近似值為何？他的『密法』策略為何？又他知道圓周率是一個常數嗎？為什麼？
結果，赫然發現有少數幾位學生竟然推斷：『祖沖之不知道圓周率是常數！』當然啦，認為祖沖之知道圓周率的學生，還是佔了絕大多數。無論如何，他們對於此一文本的內容，都提供了有趣、合理的解讀，值得有意在將古代數學文本引進課堂的教師參考。
現在，我們先來考察幾位頗有『道德勇氣』的學生，他們如何推論『祖沖之不知道圓周率是常數！』學生甲認為：
因為當時他（祖沖之）測量出來也只有說在3.1415926跟3.1415927之間，而在後面也有說明圓周率大約為22/7，也沒有辦法說出圓周率的確實值，所以他知道圓周率非為一常數。
顯然基於類似的理由，學生乙論述說：
我不認為祖沖之知道圓周率是常數這事實，因為在文本記載中看不到分數這概念，它都是敘述圓徑多少，然後圓周多少，並沒有直接說出圓周長=
×直徑。
他們的困擾，應該是來自數學上所謂『常數』的意義。
其次，我們再看看她（他）們如何認定祖沖之知道此一事實。譬如說，有學生丙說：
圓周率為一個常數，這在祖沖之的心裡一定佔有一份不小的地位，我想他應該是這樣認定的，不然他也不會發了狂似的，付出相當可觀的勞力，埋頭苦幹作了大半輩子。
同樣地，有學生丁說：
我想祖沖之應該已經認為圓周率是個常數了吧，因為如果他不認為圓周率是常數而是個會變的數字，依他的聰明才智，大概不會花那麼大的心力去求圓周率的近似值了吧，而且如果圓周率不是個常數，那他（它）的變動範圍也太小了吧，所以，根據祖沖之求得的結果來看，他應該已經確認圓周率是個常數了吧。
上述這兩個學生的認定，多少依據了歷史的事實來推論，後者當然考慮了近似值變動範圍的數學因素。不過，真正依據數學因素來推斷的，則是像學生戊，譬如他說：
我認為他知道。因為他是用內接正多邊形去逼近圓，圓直徑大小和正多邊形周長成一定關係。且在『以一億為一丈，……』這裡可知。因為『一億』是指一億等分，所以和圓大小無關。因此我認為他知道。
或者學生己：
我覺得他知道圓周率是一個常數，否則當圓的直徑改變時，圓周率也跟著變，那他所作的不就變成只是作一個特例罷了。
然而，把數學道理說得更透徹的，有可能是學生庚：
從記載中可以得知祖沖之是知道圓周率是一個常數的。因為祖沖之在計算圓周率時是把直徑變大為一丈，然後再使用劉徽割圓術的方式去求圓周，從這樣的訊息可以得知祖沖之知道圓周率是一個常數，為了方便求此常數，他將圓的直徑加大，並將正多邊形的邊數增加，以求更加接近的值。
總之，認定祖沖之知道圓周率是常數的學生認知類型，不外乎是：(1)歷史事實；(2)數學推論，以及(3)兼顧數學與歷史的理解等三種可能的方式。至於認定祖沖之不知道圓周率是常數的學生，則顯然只利用了數學的推論。至於誤判的主要原因，則是誤解了『常數』的意義所致。當然，基於歷史事實來認定祖沖之知道圓周率是常數，不能說是一種數學理解，只是一旦離開數學知識活動場域（譬如數學課堂），我們似乎就很難判斷了。
三、文本解讀
現在，我們有必要說明此一文本的意義。首先，它的作者指出『圓周率三，圓徑率一，其術疏舛』，亦即
取成3是個疏陋的近似值。請注意：此處的『圓周率』與『圓徑率』，分別指任一個圓形中，「圓周：圓徑」比（率）中的前、後項。
其實，在《九章算術》中，『率』就是這個意思。『率』的本義是標準、法度準則。因此，上一段中的所指的同一個圓之『圓周率』與『圓徑率』，就可以分別說是『圓周（長）的標準』與『圓徑（長）的標準』。如此說來，中國古代常說『周三徑一』，看起來也是一個蠻符合『標準』的說法吧！
或許，我們可以利用劉徽的注解來幫忙我們澄清：
率者，自相與通。有分則可散，分重疊則約也。等除法實，相與率也。
也就是說，凡是『相與率』的一組數，比如類似本例中圓形中的圓周與圓徑（長），那麼，它們之間一定互為質數。這可以解釋何以魏晉劉徽在求周率近似值時，他先求出徑200，周628，相約之，「周得一百五十七、徑得五十，則其相與之率也。」因此，當圓周作
倍伸縮 (
)，則圓徑亦作
倍伸縮，從而，圓形儘管大小不一，但是，各自的圓周率與圓徑率卻總是一樣。同理，正方形及其內切圓形的各自周長比為
(
取3)，前者稱為『方率』，後者稱為『圓率』，這兩個『率』也與圓形多大多小完全無關。
總之，這裡的『圓周率』與今日的圓周率不同，後者指的是『圓周：圓徑』這一個比值。這是在研讀古代中國數學文本必須特別注意的一個概念。
其次，所謂的『以圓徑一億為一丈』，是指將一丈長的圓徑分開成為一億等份，這在劉徽注《九章算術》時已經運用過了。正如同劉徽的策略，祖沖之的目的，顯然是為了利用當時已知的七個長度單位，說明『圓周率』可以逼近到甚麼程度。這七個單位依序是丈、尺、寸、分、釐、毫、秒、忽：
1丈=10尺=102寸=103分=104釐=105毫=106秒=107忽。至於『忽』有多長呢？根據祖沖之同時代的《孫子算經》的記載，『忽』代表了蠶絲的寬度。顯然，將1丈分成一億等份時，它的一份恰好是1忽，如此一來，圓周長就可以表現成到『忽』這個單位了。
因此，如果我們現在以『丈』為單位，那麼，『圓周盈數』就等於3.1415927丈，而『圓周朒數』則等於3.1415926。於是，圓率與徑率之比，就介於3.1415926與3.1415927之間了。如用現代數學符號表示，則
這也就是說，
的前六個小數位與3.1415926這小數相同，從而以3.141592為
的近似值，剛好每一位數都準確。事實上，355/113
= 3.1415920…，足見祖沖之的圓周率近似值的追求工作是相當完整的。
四、祖沖之：數學史上第五世紀的標竿人物
對於很多人來說，祖沖之並不是陌生的中國歷史人物，譬如說，在一些中國古代科學家的傳記書寫中，都可以找到他的故事，似乎不勞我們在此多介紹。不過，為了本文的完整性，我們還是轉述一些他的生平事蹟，並著重在與他的數學成就比較相關的部份。為此，我們也利用夾敘夾議的筆法，來『重建』一下有關他的歷史故事。
祖沖之
(429-500) 在中國南北朝時代的南朝劉宋朝為官，有關他的傳記相當完整，可以說明他的確作過不小的官。一般來說，平民百姓很難進入官史檔案。因此，一旦在中國歷史中找不到有關某人的文獻，我們就幾乎可以斷定他沒有作過甚麼大官。譬如說吧，三國時代數學雙雄
－
曹魏劉徽與孫吳趙爽，就都可能是名不見經傳的小人物，因此，當然沒有傳記流傳下來供我們拜讀。
祖沖之當然不同！他是范陽□縣（今河北淶水縣）人，曾祖祖台之曾任晉朝侍中，祖父祖昌開始在南朝為官，任劉宋大匠卿，父親祖朔之奉朝請。他自己則在劉宋大明六年
(462年)
擔任南徐州（現在鎮江）從事史。按此官職大約相當於地方上行政組織的科長或科員，階級最高為七品。看起來，此時他官位不高，然而，他製作《大明曆》，並推求圓周率的精密近似值，卻都是此時的工作。上引《隋書•律曆志》特別指出他此時的官銜『南徐州從事史』，或有意紀錄他的研究生涯之階段。
後來，他又升遷為婁縣（今江蘇崑山）令、謁者僕射，前者是六品與七品不定，後者掌管朝廷禮儀，是五品官。他奉命製造指南車、木牛流馬、千里船與其他奇器，大概都是此時的工作。事實上，按之史籍，南北朝時代可以說是中國奇器製造最風行的時代，至於此時中國人似乎不顧『奇技淫巧』之道德規勸，放縱巧思而製造奇器，或許可以歸之於帝王宮廷的時尚愛好，但是，整體文化的風潮走向重視個體自覺表現，恐怕也是不容忽視的因素之一。
祖沖之的多才多藝，也表現在他『當時獨絕』的『解鐘律博塞』。所謂鐘律，當然是指五音十二律的研究，由於音程與律管長度有關，所以，黃鐘律管長度的訂定，就變得十分重要。相傳祖沖之曾鑄有銅尺傳世，應該與此有關。另外，所謂『博』與『塞』是指古代兩種遊戲，今已失傳。不過，史載稱玩家需要懂一點數學，祖沖之也因善解這些遊戲之奧妙，而馳名於當時。
祖沖之的最後官職是蕭齊朝的長水校尉，是五營教尉之一，比謁者僕射還高一品。終其一生，他的大明曆始終沒有機會使用，直到他兒子祖□在南齊任官時，才獲得頒布使用，這是南齊天監八年（509年），距離祖沖之謝世已有五年，而距離他制定那一年（大明六年，公元462年），則更是長達47個年頭了。
公元462年他已經擔任南徐州從事史了。史家認為在這之前，他應該已經完成有關《九章算術》註解與圓周率的研究工作了，當時他才30歲出頭而已。在那一年之後，他似乎非常努力為官，希望在宦途上有一點作為。這或許可以解釋他何以鍥而不捨地獻上《大明曆》。在這個脈絡中，他與權臣戴法興辯論所寫的〈大明曆議〉，也見證了公元第五世紀中國歷史上的科學爭議。
〈大明曆議〉的第一段文字，說明了祖沖之自己的天文曆法研究心得，底下所引出自數學史家嚴敦傑
(1917-1988) 的白話文翻譯。一開始是有關數學的反思：
我青年時代就喜歡數學，收集了古代與近代的許多書籍，加以深湛的探討。《書經》中有關的天文資料，都覆核過。周朝和漢朝的曆法，也都檢驗過。凡是能計算的，都計算過了，並且把其中那些比較疏略的，那些比較切合的，也辨別清楚。《九章算術》中的球體積算法是錯誤的，張衡知道有錯誤而不予改正；王莽銅斛銘文上的數字用圓周率推算是有問題的，劉歆卻用錯誤數字來湊合它。這些都是數學上的大毛病。
其次，則是有關曆法的評論：
劉洪的《乾象曆》和楊偉的《景初曆》中推算定朔、定望的方法，不是測候上有問題，那麼就是計算上太繁複。這些又是曆法上的失策。鄭玄、□澤、王蕃、劉徽等人都在科學上有些成就，但他們的工作缺點也很多。我以前曾花些時間，把這些錯誤都一一更正，證據確鑿，無可非議。我是實實在在地探討前人已作過的工作，所以有小小的自信心和見識，而不凭空地推崇古人。
足見他對當時的數學與曆法，是相當熟悉的。
這裡與《九章算術》及其劉徽注有關的部分，我們有必要進一步說明。祖沖之指出《九章算術》的球體積公式
有誤（其中D是球的直徑），這是正確的描述，也間接說明他的兒子祖□證明了此一公式之背景。其實，他們父子完全是根據劉徽注解中的提示，成功地計算了『牟合方蓋形』的體積，才得以修正並證明球的體積公式。然則他何以批評劉徽的工作缺點也很多呢？我們實在無從理解，除非劉徽在曆法方面有一些研究成果，入不了祖沖之法眼。值得注意的，此一對劉徽乃至於當時天算家的評論，顯然為《隋書•律曆志》的作者所引用。
另一方面，祖沖之上引文所提及『王莽銅斛』，應該就是劉歆為王莽所鑄造的新嘉量斛。這是王莽新朝的標準量器，共有斛、斗、升、合、鑰等五種量器，其關係如下：1斛=10斗=100升=1000合=20000鑰，目前台北故宮博物院收藏了完整的一具，值得大家前往觀賞。至於祖沖之對此銅斛銘文的數字之批評，則記載在《隋書》卷十六《曆律志•嘉量》之中。根據嚴敦傑的研究，祖沖之在糾正此一錯誤時，運用了他自己的密率：
。
五、祖率
怎麼發明出來的？
追溯『祖率』這個圓周率近似值怎麼來的，我們有必要回到劉徽註解《九章算術》上。此一注文，可以說是公元第三世紀世界數學史上的重要文本之一，我在〈三國
裡袖乾坤〉一文中已有說明。不過，該文只是簡要地介紹劉徽如何利用圓面積公式『半周半徑相乘』與所謂的『割圓術』，來求圓周率的近似值3.14，而不及說明他更精緻的一些論述。
事實上，劉徽從一個直徑為二尺圓開始割圓，由內接正6邊形開始，依序計算了圓內接正12、24、48邊形之邊長，然後利用48邊形邊長，求得圓內接正96邊形之面積『三百一十三寸六百二十五分寸之五百八十四』。如用
、
分別表示圓、圓內接正n邊形的面積，則上述結果為
寸。同理，他又得到
寸。再計算
，則下列不等式成立：
或
，因此，『就一百九十二觚之全冪三百一十四寸以為圓冪之定率，而棄其餘分』，亦即圓面積近似於314（平方）寸。
接著下來，劉徽「以半徑一尺除圓冪，倍所得，六尺二寸八分，即周數。」亦即，他利用『半周半徑相乘』的圓面積公式，以求得圓周長『六尺二寸八分』：
62.8 (寸)。後來，他又「以192邊形之冪作為求率時增減的基礎」，在求得圓面積的另一個近似值：
寸。緊接著，他
佈置圓直徑自乘的方冪400寸，使它與圓冪通分相約，圓冪得3927，方冪得5000，這就是方圓之率。如果方冪是5000，則其內切圓冪是3927。如果圓冪是3927，則其內接方冪是2500。以圓半徑1尺除圓冪
寸，將所得數加倍，得6尺2寸
分，就是圓周長。直徑2尺與圓周數通分相約，直徑得1250，圓周得3927，就是它們的相與之率。如果取這值的話，大概達到非常精確的境地了。
以上這一段引文，是數學史家郭書春的白話文翻譯。其中出現了『相與之率』：3927/1250。雖然有數學史家猜測這一段文字可能來自祖沖之，但是，郭書春仍然歸給劉徽。
或許祖沖之的《綴術》也有類似的研究成果吧！可惜，本書的失傳，讓我們很難掌握直接證據以評定他的貢獻。然則『祖率』是究竟是怎麼來呢？史家紀志剛認為祖沖之可能利用了連分數的『漸近分數法』。根據此一方法，祖沖之將3927/1250、3.1415926與3.1415927表徵為連分數展開式，在分別求各自的漸近分數如下：
(1).
；
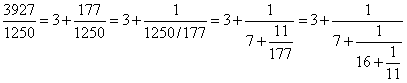漸近分數為：3/1，22/7，355，113，3927/1250。
(2).
3.1415926的連分數展開式與漸近分數：
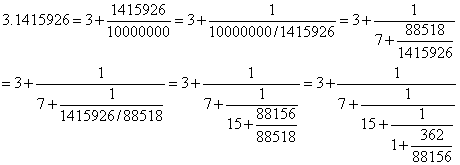
漸近分數為：3/1，22/7，333/106，355/113，86598/27565，…
(3). 模仿上述
(2)，3.1415927之漸近分數如下：3/1，22/7，333/105，355/113，
126003/40108，…
因此，紀志剛認為「從中挑選22/7為『約率』，355/113為『宻率』，是十分自然的。」為了強化此一推測的合理性，紀志剛特別指出中國古代曆家常用它以推求各種天體會合周期。譬如劉歆制定三統曆時，就利用此一方法。
其實，第五世紀的印度數學家與天文學家阿耶波多，也利用了漸近分數來解二元一次方程
（其中a, b, c都是整數）的整數解。不管當時中印數學有沒有交流，連分數展開與漸近分數的概念，似乎是第五世紀數學家都已經掌握到的重要數學方法了。附帶一提，我們今天都運用『尤拉法』來解這種不定方程，但是，此一方法實質上卻是漸近分數的概念，至於如何將一個實數展開成為（或表徵為）連分數，則本質是一種輾轉相除法。最後這個方法，在《九章算術》乃至更早的《算數書》（公元前186年）都已現身，可見古代中國人提出『漸近分數法』的歷史條件，到了東漢之後應該已經成熟了。
六、結論：如何書寫、閱讀祖沖之？
由於祖沖之的《綴術》在宋代已經失傳，所以，他如何求得『祖率』，才會成為數學史上的千古懸案。本書在唐初，曾由李淳風等註釋、輯入所謂的《算經十書》，作為國子監太學明算科（有一點像現代的國立大學數學系）的教科書，其他九部有《周髀算經》、《九章算術》、《海島算經》、《孫子算經》、《張丘建算經》、《五曹算經》、《五經算術》、《夏侯陽算經》與《緝古算經》。現傳的《算經十書》，則是宋代刊刻時，以《數術記遺》補上前九部而成。至於失傳的原因之一，據說是內容過於艱深所致，它在明算科中必須修習的時間最多
─ 高達四年，讓很多師生望而卻步。
儘管如此，我們從《九章算術》劉徽注以及《隋書•律曆志》的文本，應該足以『重建』祖沖之推求圓周率的過程，尤其是針對他如何找到『祖率』。這些『理性重建』的工作，當然可以幫助我們閱讀祖沖之！問題是：我們的最佳切入點是什麼？
一般來說，傑出人物的傳記如果故事說得動人，對於讀者應該具有人格的薰陶作用，尤其是如果涉及傳主的科學知識活動如何受到『不當』的壓制，則更有科學普及所標榜的『啟蒙』價值。這是敘事的部份，任何一種科學家傳記書寫都不會錯過。然而，以祖沖之為例，他與權臣戴法興有關『大明曆』的科學爭議，恐怕仍有待新的史學觀點與研究才能釐清。平心而論，對於祖沖之來說，『大明曆』的重要性遠遠大於圓周率的推求。這是因為前者絕對是國家大事，至於算學研究呢，請不要忘記（南齊）顏之推的見證，他在《顏氏家訓》中告誡顏家子孫：「算術亦是六藝要事，自古儒士論天道、定律曆者皆學通之。然可以兼明，不可以專業。」
不過，這個社會文化脈絡，倒是反過來更證成了祖沖之算學研究的難能可貴。儘管『祖率』可能並不是祖沖之一生中最想珍視的成就，但是，他畢竟因而在數學史上不朽！所以，如果我們希望通過歷史的書寫與閱讀，向祖沖之『學習』，那麼，他如何推求『祖率』的過程，絕對是最值得還原的題材之一。這也是數學家傳記書寫不可缺少的『認知』面向。只要對這一點無暇顧及，那麼，所謂的『祖沖之傳』與其他一般歷史人物的傳記就很難區隔，連帶地，也就難以呈現相關的數學知識之趣味與特色了。
是的！我們非常希望下次再讀到『祖沖之』時，可以發現書寫者在適當的『脈絡』中討論『祖率』的認知意義，而不只是以『消費文化符碼』的方式，『徒然地』說它準確到小數點後第六位：3.1415926等等、等等
……。
參考文獻
洪萬生
(1982).〈重視證明的時代：魏晉南北朝的科技〉，收入洪萬生主編，《格物與成器》（台北：聯經出版公司），頁105-163。
洪萬生 (待刊稿).〈三國
裡袖乾坤〉。
紀志剛 (2000).《南北朝隋唐數學》，石家莊：河北科學技術出版社。
郭書春 (1995).《古代世界數學泰斗
― 劉徽》，台北：明文出版社。
郭書春 (1998).《九章算術譯注》，瀋陽：遼寧教育出版社。
嚴敦傑 (2000).《祖沖之科學著作校釋》，瀋陽：遼寧教育出版社。
附錄I：
如何解讀下列有關祖沖之的文本？
《隋書•律曆志》有如下之記載：
圓周率三，圓徑率一，其術疏舛。自劉歆、張衡、劉徽、王蕃、皮延宗之徒，各設新率，未臻折衷。……
祖沖之更開密法，以圓徑一億為一丈，圓周數盈數三丈一尺四寸一分五釐九豪二秒七忽，朒數三丈一尺四寸一分五釐九豪二秒六忽，正數在盈朒二限之間。密率：圓徑一百一十三，圓周三百五十五；約率：圓徑七，圓周二十二。
請問祖沖之的圓周率近似值為何？他的『密法』策略為何？又他知道圓周率是一個常數嗎？為什麼？