三大作圖題

西松高中 蘇惠玉老師

一、楔子

平面幾何作圖中，有很大一部份是尺規作圖。所謂的『尺規作圖』，即是限制只能使用沒有記號的直尺和圓規，在紙上有限次作出曲線。

在國中所教授的平面幾何中，尺規作圖是其中的一個單元，但是，在學習的過程中，學生對尺規作圖的瞭解、重要性或是趣味性，可能都是一知半解，或毫無體會。筆者曾問班上的高二學生，為何『倍立方問題』沒有辦法用尺規作圖解決？學生的回答居然是「當時沒有圓規」！當然，他們對尺規作圖的限制也不是很清楚。

筆者想利用這一篇文章，從尺規作圖的限制談起，看看古典希臘時期研究數學的學者，在那樣的由文化所形成的條件下，對所謂『三大作圖題』的解決所做的努力，並從中一窺數學在條件限制下的解題樂趣，藉以提供教學上的一盞探照燈，照出一條不一樣的教學路徑。

二、幾何作圖的意義

為什麼作圖要有這樣的限制？首先，從希臘的學術風潮來看。泰勒斯 (Thales, 640~546 B.C ) 將數學抽象化思考，以及用演繹式證明某些定理，將包含數學在內的哲學，從實用領域提升到思辯的層次。後來，柏拉圖認為數目和幾何觀念是不存在於物質層面的，是超乎經驗而存在的，以『形式』（Form）存在於某一個理想世界中。對他而言，學習數學是一種「再發現」的過程，他想要去掌握或瞭解自然界現象外永恆不變的真理，數學則為他提供了一條路徑，他在《共和國》(Republic)中，藉由蘇格拉底的話語，道出了他的數學哲學觀點：

……有一種知識是我們不可或缺的。我們所追求的這種知識有兩種用途，一種是軍事上的，另一種是哲學上的。因為打仗的人必須研究數目，否則便無法整頓隊伍。哲學家們亦然，他們需要在浩瀚多變的知識領域中，尋找真理並緊握它們，所以他必須同時是一個數論家。……我們必須盡力勸勉城邦未來的領袖學習數論，不僅僅是業餘學習，要不停的學習，直到能夠用心靈來體會數目的存在為止。……領袖們必須為軍事用途和自己的靈性研讀數學，也因為這是使他們能辨別真理和存在的捷徑。

換言之，柏拉圖認為：數學家們要確實掌握一些用心靈的眼睛才能看記得東西。現實世界中的一切，只是理想世界中「理形（ideal）」的不完美倒影而已，唯有透過數學嚴謹的訓練，才可能掌握不斷變化的自然現象背後的永恆不變的真理。所以，只要有圓和直線這兩個柏拉圖認為最簡單、最完美的圖形，應該就足以描繪其他的圖形了，而且，若允許使用其他的機械工具，那麼，感覺成分將多於思考成分，從而就顯得膚淺且幼稚了。

        亞里斯多德原本是柏拉圖的學生，但是他對數學的看法與柏拉圖並不一致，亞里斯多德對眼前存在的物理世界比較關切，他認為數目和幾何也是物體的屬性，數學研究的對象存在於物質世界中，是從物理實體上面所引出來的抽象觀念。而亞里斯多德的主要成就之一，即是為邏輯科學奠定基礎。他討論過定義的問題，認為一系列的定義必須有起點，且定義的概念都必須存在，他以作圖來證明概念的存在。他還處理了數學的基本原理，區分出公理（對所有學科都真）和設準（某一學科可接受的第一原理）的不同。

        這些規範都在歐幾里得的《幾何原本》(Elements)中獲得體現。本書無疑是古典希臘時期集大成的一本重要著作，它的格式與風格，也是古希臘數學文化的一個典範。《幾何原本》共十三冊，以最簡單的二十三個定義，五個公理 (common notion)，五個設準 (postulate) 為基礎，共四百六十五個命題，以命題間的邏輯順序演繹證明。其中五個設準如下：

        1.          從任一點到任一點可作直線 ([T]o draw a straight line from any point to any point)。

        2.          有限直線可沿著直線不斷地延長 (To produce a finite straight line continuously in a straight line)。

        3.          以任意中心與任意距離可作一圓 (To describe a circle with any centre and distance)。

        4.          所有的直角均相等 (That all right angles are equal to one another)。

        5.          若兩直線為一直線所截，使得一側之同側內角和小於兩直角，則將兩直線延伸，必在此側相交 (That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.)。

所謂的『設準』，即是「假設它是對的 (Let the following be postulated)」，在這樣一個前提之下，在設準的1~3中，確定了歐幾里得使用工具作圖的基礎，再加上第一冊的命題3，在歐幾里得《幾何原本》對整個西方數學的強烈影響之下，『尺規作圖』的規範或限制，一直沿用至今。

三、三大作圖題

        所謂的『三大作圖題』，即是：1. 化圓為方；2. 三等分任意角；3. 倍立方這三個尺規作圖的問題。數學家們在經過幾世紀的努力，與數學這一門幾世紀的進展，已經證明這三個問題在尺規作圖的限制之下無法作出。但是，希臘數學家面臨這個問題時，並不知道這樣的結果。他們嘗試去解決這三個問題，在尺規作圖的限制之外，另闢蹊徑，這些小徑或許不是花團錦簇，結實纍纍，卻也仍有其可供欣賞之處。

四、化圓為方問題

        所謂『化圓為方』 (to square a circle)，即是做一正方形使其面積等於一已知圓面積。正如前述，希臘人醉心於這個問題，是整個文化影響的結果。例如，希臘時期有許多等面積作圖問題；將不規則形狀化成規則、對稱的正方形等等。研究化圓為方問題最有名的，即是希波克拉提斯 (Hippocrates of Chios, 約460~380 B.C) 的「新月形的平方化」。因為那時代，已知任意三角形可以化成直角三角形（面積相等）；直角三角形可化成長方形；長方形又可化成正方形，所以，如果兩圓相交部分的新月形，可以化成面積相等的三角形的話，整個問題即可獲得解決。

        根據第五世紀時的Simplicius引述Alexander Aphrodisiensis的話，認為有兩個新月形可以歸於希波克拉提斯。第一個新月形如圖，AB、AC為內接於圓AB的正方形的兩邊，弧AEC為以AC為直徑的半圓，Alexander證明：新月形ACE＝ 。

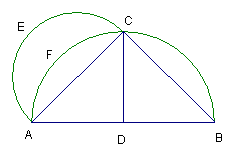因為AC＝BC，又AB²＝AC²＋BC²，所以，
AB²＝2AC²

又 ，所以

半圓AEC＝ 圓ADCF，

同時減去弓形ACF，所以新月形ACE＝ 。

        第二個新月形如圖，AB是半圓的直徑，CD＝2AB為一半圓的直徑，CE、EF、FD為正六邊形的邊，且CHE、EGF、FKD分別為直徑CE、EF、FD上的半圓。Alexander證明：

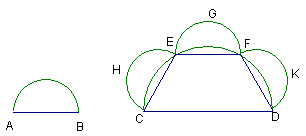新月形CHE＋新月形EGF＋新月形FKD＋
半圓AB＝梯形CEFD。

因為梯形CEFD＋三個以AB為直徑的半圓＝以CD為直徑的半圓＋三個新月形，

又CD＝2AB，所以，

以CD為直徑的半圓＝4（以AB為直徑的半圓），相消後，

梯形CEFD＝半圓AB＋三個新月形（CHE、EGF、FKD）。

接下來Alexander說，因為一個新月形已經證明等於一個正方形，所以從可以正方形化的梯形中，減去等於三個新月形的正方形，剩下的圓亦可正方形化。

        這兩個新月形平方化的證明過程中，錯誤是相當明顯的。第一個新月形是一個特殊化的新月形，在圓內接正方形的邊上，只能說這樣的新月形可以平方化；而第二個新月形，卻是在圓內接正六邊形的邊上；根據史學家Ivor Thomas的說法，希波克拉提斯不太可能會犯這樣一個明顯的錯誤，所以，我們只能對Alexander的說法存疑。

        作一正方形使其面積等於一已知圓的這個問題，其實牽涉到π與 尺規作圖的可能性。1882年德國數學家林德曼 (F. Lindemann, 1852~1939) 在『代數數』與『超越數』的基礎下，證明π為超越數，因而不可能利用尺規作圖作出此數，同時，得證『化圓為方』是不可能的。

但是，如果不限制用尺規作圖的方法、或要滿足尺規作圖的設準的話，就有許多的解法了。簡單的如眾所皆知的達文西（Leonardo da Vinci, 1452-1519）的妙用，他取一圓柱，底面積與已知圓相等，高為半徑的一半。將這個圓柱在平面上滾一圈時，產生一個面積恰為 的長方形，再將矩形化為正方形即可。另外還有其他如希皮亞斯 (Hippias of Elis, 約420B.C) 的割圓曲線 (quadratrix)。

        所謂的『割圓曲線』如圖。ABCD為一正方形，一線段，起始位置在AB，繞著A點從AB的位置，以固定的角速度旋轉移動到AD；第二條線段起始位置也在AB，平行AB地以固定的速度垂直向上到DC；第一條線段與第二條線段同時分別到達AD與DC，每一個時刻，這二條線段都會有一個交點，這些交點所成的圖形即是所謂的割圓曲線。換句話說，割圓曲線上任一點X必須滿足

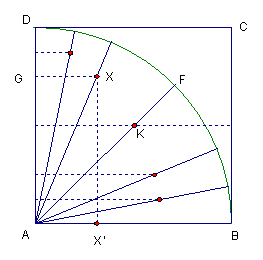
        『割圓曲線』同樣可以解決化圓為方的問題。根據Pappus（約A.D 320） 的說法，Dinostratus (約350B.C)使用了割圓曲線，來解決化圓為方的問題。要解決這個問題，首先必須證明在割圓曲線中，

，即

這裡Pappus用了阿基米德常使用的兩次歸謬證法：證明大於與小於都不成立。由於證明過程過於冗長，此處略過不述。上述式子成立，代表四分之一圓的弧長q可以作圖得出，那麼，圓的周長就可作圖。接下來，Pappus認為Dinostratus應該知道圓的面積，可以表示成以圓周和半徑為兩股的直角三角形，所以，圓可化成直角三角形，直角三角形又可化成正方形，所以，就解決了化圓為方的問題了。不過，我們千萬不能忘記：此處用到的割圓曲線，無法利用尺規作圖作出。

利用『割圓曲線』同樣也可以輕易的解決三等分角的問題。三等分任意角 時，只要三等分相對的線段GA即可。

五、三等分任意角問題

        希臘人會試著去三等分任意角，可能是角的平分之後的延伸。許多希臘數學家在這個問題上，發明了許多的「程序」去三等分一個角，其中包括阿基米德 (Archimedes, 287-212 B.C)及尼可門笛斯 (Nicomedes, 約240 B.C)。

        阿基米德在他的《引理集》(Book of Lemmas)的命題8寫道：

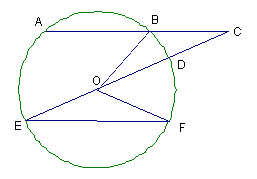如果AB是以O為圓心上的任意弦，AB延長到C，使得BC等於圓的半徑；如果CO交圓於D並延長到交圓於第二點E，則弧AE等於3倍的弧BD。

證明：作弦EF平行AB，連接OB，OF，
因為角OEF＝角OFE，

所以，角COF＝2角OEF

             ＝2角BCO（由平行）

             ＝2角BOD（因為BC＝BO）

所以， ，弧BF是弧BD的3倍。而弧AE等於弧BF，所以，弧AE是弧BD的3倍。

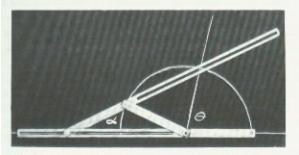
        這個命題可以轉化成三等分角的問題：弧AE所對的圓心角，為弧BD所對的圓心角的3倍。但是，問題在於：若AE為給定的弧，延長CO時不見得會交於E點，所以，我們無法用尺規作圖解決。如果不考慮尺規作圖，阿基米德的這個命題可以作 出一個工具來解決三等分意角的問題：

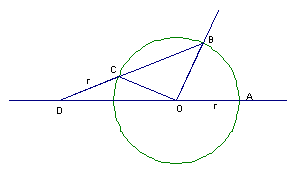
將阿基米得的命題轉換成下圖， 為給定的任意角，過B作一直線，交圓於C，同時交AO直線於D，使得CD＝半徑r，則 。按照右圖，在一棍子上固定出C與D點，CD長度＝半徑r，移動棍子，使得棍子交圓於B點。

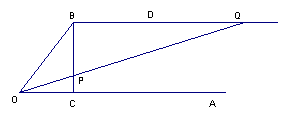        三等分任一角的另一解決途徑，為尼可門笛斯的方法。如圖，角AOB為給定之角，過B作AO的垂線，交AO於C，作直線BD平行AO。在直線BD上找一點Q，連OQ，並交BC於P，使得PQ＝2OB，則 。

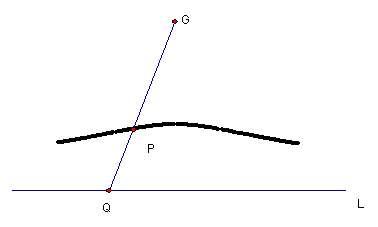
此時作圖的問題在於Q點的決定，尺規作圖並無法作到。但是，尼可門笛斯作了一個新的曲線來解決這個問題，即是所謂的『尼可門笛斯蚌線』(conchoids of Nicomedes)。如圖，若在一根直棍上標示P、Q兩點，PQ的長度為d，將這直棍繞著一點G旋轉，同時Q點在另一直棍L上滑動，P點所成的軌跡即是所謂的蚌線（現今的蚌線定義還有另一部份，在L的另一邊）。若將上圖中的O點訂為G點，直線BD為L，P點為蚌線和垂直線BC的交點。

        在希臘時期，雖然已經可以用不同的曲線來三等分任意角的問題，例如割圓曲線和蚌線，但都不符合尺規作圖的規定。尺規作圖的不可能性的證明，要等到三次方程式的相關理論完成後才能證明，同時，這也能證明了倍立方問題的不可能。在這證明過程中，數學家利用到二個理論：1. 一個三次方程式若無有理根，則無『可尺規作圖根』。2. 一次因式檢查法。藉由尼可門笛司解決方法，如下圖，因為 ，所以

而因為 為等邊三角形，BO＝BR，所以，E為OR的中點，即

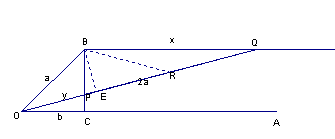ER＝ OR＝ ，

且EQ＝ER＋RQ＝

故， ，得到一三次方程式 。

若三次方程式有可作出的根x，則BQ可作，Q點決定後，三等分問題即可解決。所以，由上述可知，可否三等分和b的值有關，有相當多的角是可以三等分的，例如，b=0，即角為90⁰時可三等分，但是，例如 ，即角為60⁰時，方程式為 ，並沒有有理根，所以，所有的根皆是不可尺規作圖的，即60⁰無法尺規作圖三等分，也就是說，尺規作圖三等分任意角（除了直角等幾個特別角之外）是不可能的。

六、倍立方問題

關於倍立方的問題，有一個傳說是這樣說的，克里特國王Minos要為他的兒子Glaucus建一座立方體形狀的墳墓。但是他聽說建好的墳墓只有每一邊100呎，他覺得太小了。 “It must be doubled in size.” (體積必須是現在的兩倍)，他要求建築師盡快將每一邊都加倍。很快地，數學家們就發現錯誤所在了，並且思索著解決之道。

另一個傳說，則是關於Delos這座小島的問題。所以，倍立方的問題有時會稱為Delian problem。阿波羅藉著一位先知命令提洛島民，要將他的立方體形狀的祭壇體積加倍，並且保持形狀。他們作不出來，就將這個問題拿去問柏拉圖，柏拉圖告訴他們說，阿波羅給出這個命令，不是因為他要一個兩倍大小的祭壇，而是他要藉著這個苦差事，來強調數學的重要性。

        將一個邊長為a的正立方體體積加倍，即是要作出一新的正立方體之邊長x，滿足 。這個問題被希波克拉提斯歸結為作出兩線段長a與2a的兩個連續比例中項。也就是說，要作出兩線段x, y滿足

x即為所要求的新正立方體的邊長。希波克拉提斯如何想出這個倍立方問題的兩個比例中項解法，並沒有詳細的記載。據推測，他可能是這樣想的：將兩個邊長為a的正立方體放在一起，成為一個立方體長寬高分別為2a, a, a，體積為2a³；想向將這個立體拉整一下，使其成為高維持為a，長寬分別為x, y的立方體，因為體積要維持一樣，所以 ，從中可發現 ；再將立方體拉整成長為x，寬與高亦為x的立方體。同樣，體積要維持一樣，所以 ，或 。故， 。

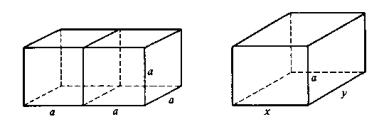
希波克拉提斯的發現並沒有解決倍立方的問題，只是將問題轉換成另一形式而已。但是，如何作出兩個比例中項x與y呢？Menaechmus (約350B.C.) 引入新的曲線，即圓錐曲線來解決這個問題：

將連比例式拆成兩個等式： 及 ，從此，可得方程式 （或是 ），及 （或是 ）。因為a已知，所以兩個拋物線的頂點、對稱軸能決定出，即兩拋物線的交點可作出，即x與y可作出。

『圓錐曲線』當然不能用尺規作圖作出，要證明倍立方問題的不可能，也只要用到上述的三次方程次理論即可。設原立方體的邊長為1，要作出的立方體邊長為x，則x要滿足 ，這個方程式沒有有理根，當然就沒有可尺規作圖的x了。

七、結語

        在本文中，筆者舉出了希臘時期許多三大作圖的『解決』之道，當時數學家們對這些問題有興趣，嘗試在尺規作圖的限制下，解決這些問題。儘管他們未及得知無『不可能』的答案，卻依然能創造出許多有趣的、新的曲線來試圖解決問題。他們的思路過程或是結果，都能成為我們教學時的另一角度的思考與策略。

參考文獻

Euclid (1956). The Thirteen Books of the Elements, translated with introduction and commentary by Sir T. L. Heath. N. Y.: Dover Publications, Inc.

Calinger, R. ed. (1995). Classics of Mathematics, New Jersey: Prentice-Hall, Inc.

Bunt, Lucas N. H. et al eds. (1988), The Historical Roots of Elementary Mathematics. N. Y.: Dover Publications, Inc.

Heath, T. L. ed. (1897). The Works of Archimedes, N. Y.: Dover Publications, Inc.

Kline, M. (1983).《數學史—數學思想的發展》(林炎全、洪萬生、楊康景松譯)，台北：九章出版社。

Dunham, W. (1995).《天才之旅》(林傑斌譯)，台北：牛頓出版社。

梁宗巨 (1992).《數學歷史典故》，台北：九章出版社。

蘇意雯(1999)，〈數學哲學：柏拉圖vs. 亞里斯多德〉收錄於《HPM通訊》第二卷第一期。