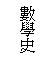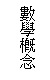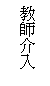『數學期望值』學習工作單

                                                        北市成功高中 蘇慧珍老師

一、前言

在一堂數學課中，教師呈現給學生的，往往有專業的理論以及教師的權威。在這裡，我所指的權威是「老師說，學生聽」的教學模式。如果想要營造活潑的教學環境，相信教師必須提供學生可熱烈討論的問題，而所提出的問題對於學生的單元學習若能有所幫助，自然是最佳的學習情境。為嘗試達到此目標，筆者在『數學期望值』單元教學時，特別挑選歷史上幾位數學家們對於『賭金分配』的幾種方法，引發學生的探索興趣，希望能經由一連串的討論，讓學生們對於數學發展具有參與感，並能從數學家錯誤的解決方式中，試著了解自己的學習困難之癥結所在。

二、教學指引

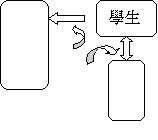
    『賭金分配』曾引發一連串歷史上不同時代數學家的熱烈討論。筆者希望能將這些重現於教室中，鼓勵學生成為為主動學習者，而教師則擔任觀察者及協調者。不過，教師的適時介入與引導，卻是很重要的關鍵。筆者所希望達成的教學過程，以圖略表如下：

    至於實施方法，則是由教師提問之後，讓學生討論各種解法之可行性。可想而知，學生們的看法必定會有不同處，此時的討論就是一種社會化的過程。同時，透過討論，學生可以檢視自己的想法，讓概念得到更多的澄清。另一方面，在與歷史上的數學家之經驗連結之後，學生或許可以了解數學並非一蹴可幾，而是一種循序發展的文化。同時，學生本身會犯的錯誤，也可經由歷史重現的方式找到盲點，進而獲得改善的機會。

筆者認為，本張工作單的作用，在於鞏固學生對於機率的基本概念，亦即『機會的均等與否』的討論。不過，或許我們可以先追溯這些相關概念的歷史淵源。

三、歷史回顧

        機率論的起源之一為賭博問題。在15~16世紀中，義大利數學家帕西歐里(Luca Pacioli)、塔爾塔利亞 (Niccolo Tartaglia) 和卡爾連奇 (Fillipo Carlandri) 的著述中，都曾討論過『如果兩個人賭博提前結束，該如何分配賭金?』等機率問題。其中，帕西歐里的著作《大全》(Summa de arithmetica geometria proportioni et proportionalita)，就有如下一題：

兩球隊比賽聲明投進一球得10分，先得60分者獲勝。但是比賽途中因為有狀況發生，導致無法賽完，此時一隊得50分，而另一隊得30分，試問該如何分配賭金？

以上的情況，當然必須假設兩隊是實力相當的。帕西歐里的解法是根據以得分的比例作分配，意即50：30＝5：3。塔爾塔利亞在他的著述General trattato di numeri et misure中，批評帕西歐里的解法有誤。他注意到，若是其中有一隊得0分，則他們將無法分得賭金，而這樣的分法是不公平的。

    卡爾連奇也一樣在他的著述中，使用了類似成比例的分法。但在其他文件中，我們發現，他使用了另一種不同的解法，筆者舉例說明如下：若討論與上述相同問題，有一隊需再得10就贏得比賽，而另一隊則需再贏得30分就贏得比賽，因此，分配賭金以其所再需要分數反比分配， 。就我們現在的解法去檢驗它，答案當然是錯誤的。

    其後的約兩百年間，許多其他數學家也分別給出了許多解法，但是，卻遲遲無法為機率論揭開神秘的面紗。

四、巴斯卡與費馬的通信

在1654年左右，愛好賭博的法國人米爾 (Chevalier de Mere) 向巴斯卡(Blaise Pascal) 提出了類似的分配賭金問題，引發了巴斯卡與費馬 (Oeuvres de Fermat) 之間探討機率問題的多封通信。在通信中，他們利用組合方法給出了這類問題的正確答案，從而在機率論中創立了一些基本結果。米爾的問題如下：

兩人比賽各出資32金幣，規定必須要贏三局才能贏得賭金，但後來比賽因故終止，且勝局比為(1,0)，問此時應如何分配賭金？

巴斯卡依序考慮兩人勝局比 (2,1)，(2,0)，(1,0)。首先分析 (2 , 1)，若繼續比賽，如果第一位贏，則比局 (3 , 1)，他將拿走全部的賭金；如果第二位贏，則比局 (2 , 2)，每個人均分所有金幣，即32金幣。因此，第一位至少將得到32金幣，而剩餘均分即16、16，所以，比賽終止時的分法為 [32＋16,16]，亦即 [48 , 16]。

接下來，分析 (2 , 0)。若繼續比賽，如果第一位贏，則比局 (3 , 0)，他將拿走全部賭金；如果第二位贏，則比局 (2 , 1)，由上述結果可知，第一位將拿走48金幣。因此第一位至少將得到48金幣，而剩餘均分即8、8，所以終止比賽時的分法為 [48＋8,8]，即 [56 , 8]。

最後，分析 (1 , 0)。若繼續比賽，如果第一位贏，則比局 (2 , 0)，由上述結果可知，第一位將拿走56金幣，第二位將拿走8金幣；如果第二位贏，則比局(1 , 1)，每個人均分所有金幣。因此，第一位至少拿到32金幣，第二位至少拿到8金幣，剩餘24金幣，兩人均分即12、12，所以，終止比賽時的分法為 [32＋12,8＋12]，即 [44 , 20]，比例即為44：20＝11：5。

        費馬的解法，是考慮最多還需要幾場比賽才能看出贏家。如果第一位需要再比m場才贏，第二位需要再比n場才贏，則最多需再經過m＋n－1場比賽即知結果；例如米爾問題中，兩人勝局比數為(1 , 0)，則第一位需再贏2場、第二位需再贏3場即知結果，因此，兩人最多再比2＋3－1＝4場比賽，考慮此四場結果如下（a代表第一位獲勝，b代表第二位獲勝）：

  aaaa (1)   aaab (1)         aabb (1)          abbb (2)          bbbb (2)

            aaba (1)        abba (1)          bbba (2)    

            abaa (1)        bbaa (1)          bbab (2)

            baaa (1)        baab (1)          babb (2)

                          baba (1)

                          abab (1)

        由上述可知，兩位應該分的比例為11：5，此結果與巴斯卡的答案相同。但是，法國數學家羅貝瓦爾 (Gilles de Roberval) 卻持不同的看法，他認為有些比賽不需要列出四場，而只需二、三場則可得結果。

        費馬的解法扯出巴斯卡的二項式定理，亦即：若把a，b是為兩項，其四次展開式為 ，其中係數為1、4、6、4、1，因此，分法為（1+4+6）：（4+1）＝11：5。（很神奇吧！）

荷蘭數學家惠更斯 (Christopher Huygens) 訪問巴黎時，了解到巴斯卡與費馬的通信研究，對這類問題產生興趣，後來，他撰寫《骰子遊戲》(Dice Game, 1657) 來探討機率問題的原理，其中包含許多習題，被許多人認為是機率史上第一本教科書。

五、工作單的設計理念及細部分析

    筆者將『賭金分配』問題設計如下：

若有兩人各出資賭金96金幣，規定必須要贏三場者才能贏得全部賭金192金幣，但比賽中途因故終止，且此時勝局數(甲:乙)為（2:1），問此時應如何分配賭金？（甲乙兩人實力相當）

賭金的多少，取決於是否能夠被32及3整除。（原因留待後文說明！）筆者一開始並不引述歷史上的問題吸引學生，而是稍加改良後再加以提問。有關具體實施方式，筆者認為有兩種：

1. 提問後，由學生開始討論其解法應為何，教師並適時指導。

            2. 提問後，以隱匿作者名字方式舉出各種解法，讓學生判別各解法之可行性。

筆者決定採用第二種，原因在於本校每班學生在外補習人數約有一半，關於賭金分配問題以機率求其解的方式，有些學生會『毫無猶豫』（亦即：未經深思）地提出，而且，我也擔心他們會局限於所學，因此，最後決定採用第二種方式：一方面讓學生可以欣賞其他解法，另一方面，筆者也有意藉此觀察學生的觀念是否正確。

    筆者分別採用帕西歐里 (A)、卡爾連奇 (B)、費馬 (C)、巴斯卡 (D) 的解法，並將其匿名引用依序如下：

A：賭金分配應就其勝局比數，即2:1，依比例分配，甲應分得 金幣，乙應分得 金幣。（由於賭金被3整除較好討論，因此，筆者將其賭金設定為被3整除之數。）

B：其賭金分配應考慮若不終止比賽，兩人各須贏幾場，按其各須贏得場數反比分配；即甲已贏2場，須再贏一場就可獲賭金，而乙已贏1場，須再贏二場就可獲賭金，因此，甲所需場數：乙所需場數＝1:2，故其反比為 ，由此可知，甲應分得 金幣，乙應分得 金幣。

C：根據至多需要幾場比賽才能看出贏家，如果甲需要再比m場才贏；乙需要再比n場才贏，則需再經過m＋n－1場才能宣布贏家。以勝局比為（2:1）為例，接下來的二場比賽可能結果列出如下：

（a代表甲勝，b代表乙勝）

           aa           ab           ba          bb

         (甲勝)        (甲勝)       (甲勝)       (乙勝)

所以，兩人應該分的賭金比列為[3：1]，即甲可得 金幣，乙可得 金幣。

 D：甲贏兩局，乙贏一局，在擲下一次骰子時，若甲贏了，他將得到全部192枚金幣；若乙贏了，他們所贏局數比為2：2，在這種情況之下分賭金，每人將拿回自己的96枚金幣。綜上所述，若甲贏了將得192枚金幣，乙將獲得0金幣；若甲輸了則會拿到96枚金幣，乙會拿到96金幣，因此，甲至少可拿到96枚金幣，乙至少可拿到0金幣。假如他們不繼續賭下去的話，可將96枚金幣先給甲，至於剩餘的96枚金幣，可能甲得，可能乙得，機會是均等的，所以，甲乙兩人均分剩下的96枚金幣，各得48枚，亦即：甲乙兩人所得金幣各為[144；48]。

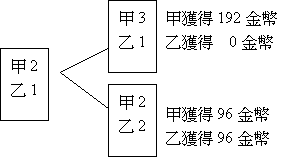
若今甲贏兩局，乙贏零局，中途停賽而分配賭金，結果應如下：

 由上圖知，甲至少獲得144金幣，乙至少獲得0金幣，而剩下48金幣，可能甲得，可能乙得，機會是均等的，因此，由兩人均分，於是，甲得144＋24＝168金幣，乙得0＋24金幣。

六、實施情況分析

     首先，筆者要求每位學生（在課餘時間）寫下他們自己覺得A、B、C、D四人的方法可行性如何，再利用課堂時間引領學生討論，最後，揭開此四人的真正身分，希望藉以了解此一工作單如何對機率觀念的導正、加強有所幫助。

     針對A、B、C、D四人的解法，筆者設計問題如下：

問題1. 請問你認為A的分法可不可行？請說明（可舉例）。

問題2. 請問你認為B的分法可不可行？請說明（可舉例）。

問題3. 請問你認為C的分法可不可行？請說明（可舉例）。

問題4. 請問你認為D的分法可不可行？請說明（可舉例）。

問題5. 利用你所學過的機率，此賭金分配問題應如何解？為什麼？

實施對象有兩班，甲班有42人，問卷共回收35份；乙班有43人，問卷共回收33份。針對此68份問卷，筆者整理結果如下：

關於問題1，學生認為不可行的有68份，達100％，其理由分別有：

      •應就獲勝機率來分才公平，不可直接比例分配。

    •沒考慮到甲和乙勝局有哪些可能，以及往後甲勝或乙勝的可能和場數。有可能甲會在第四場或第五場才勝，以只有在第五場才勝，之後的機率也要考慮進去。

      •因為有一方先贏三場即停止，所以要分場次討論。

    •若今比數2：0，則甲得192金幣，乙得0金幣，不合，因不知最後獲勝是誰。

      •應從接下來甲和乙個別贏得這場比賽的機率來分配。

    •應考慮樹狀圖 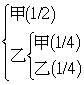  ，所以甲應得 ，乙應得 。

    •從他們出資賭資開始，甲和乙勝負機率各半，不應以某時的比數來決定如何分配賭金，故甲拿96金幣，乙拿96金幣。

    由上述各答案可知，有些學生侷限於所學，依所學方法之答案去判別A的方法錯誤與否（在此筆者並不認為此種說明不好）；有些學生認知到，A的方法欠缺考慮到未來甲、乙的可能性如何；有些學生找到以此種方法分配賭金的不公平之處（舉例如：某一方勝局場數為0時。）。在此，可以看出雖然每位學生都認為A（帕西歐里）的方法不可行，但理由卻各有所不同。值得高興的，在聽了幾位同學的理由後，大部分學生都能夠接受與認同，並有一些原本只是以答案不合之理由回答的學生，最後也都了解：帕西歐里的方法除了與他們自己所認知的答案不同外，其不周全的地方在哪裡。

關於問題2，學生認為可行的有9份，達13.25％，其理由分別有：

  •因為在接下來的全盤勝之機率目前甲＞乙。

  •因為這乙分的錢會比本來的多。

  •因為甲贏一場與乙贏二場的機率為 ，即為所需場數之反比 ，所以可行。

有些學生認為可行卻沒寫下理由，在追蹤之下，他們覺得既然舉不出反例，因此認定此法可行。另一方面，學生認為不可行的有59份，達86.75％，其理由分別有：

  •應從機率，而非場數。

  •因為次法忽略了接下來勝負場次的各種可能情況。

  •甲以贏兩場，若之後的情況為

甲贏： ，   乙贏、甲贏： ，  乙贏、乙贏：

所以，甲應得 ＋ ＋ ＝144。

  •他沒考慮到每場得勝的機率的不同，將每場視為相同機率。

  •因為在此用『反比』沒有任何邏輯，但比A進步，有考慮到後續。

  •若由這種方法，則忽略了之前二人勝的場數，思慮不周，所以不行。

  •因為在接下的第一場勝，和第一場敗而第二場勝的機率不均等，所以，不可以合在一起算。

  •因為勝有先後順序不同。

  •為何用反比？沒有依據。

  •今若先勝10局得金，甲勝：乙勝＝7：4，所以賭金分配甲得：乙得＝

甲勝機率比乙勝機率大的多，賭金卻拿到甲之一半。

此外，有些學生觀察到，雖然B (卡爾連奇) 已經考慮到未來甲乙兩人的比賽，但實際上後來的比賽情形如何，B並未討論，而且其中所用『反比』的方法，讓人覺得沒有依據，只是為了規定而規定的，沒有說服性。筆者發現：少部分認為可行的學生，在機率方面學習成就較低。

        關於問題3，學生認為可行的有54份，達79.41％，其理由分別有：

    •兼顧到所須場數和勝算的關係，不管是乙先贏一場甲再贏，或甲贏第三場的情形，都考慮周到，對甲、乙都公平。

     •乙勝機率： ，所以甲勝機率： 。

    •可以，但應是置多需要m＋n－1場才能宣布贏家，而不是剛剛好m＋n－1場，原來多的那一場只是可以較好算而已，而接下來的分配方法，因以把所有的結果列出來，所以可以。

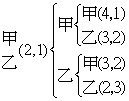    • ，正常甲贏三場就結束但若考慮所須場數而繼續，則期望值相同。 ，所以依然為甲：乙＝3：1。

    •我認為這也像是『紙上』比賽下去，這樣會使機率更接近，這樣分配應算是可行的。

    •可算出答案，但並非正確解法，因不可能出現aa的情況 (甲到第三場就贏了，不須再比第四場。

•雖然接下來的兩場中，甲贏一場便停止，沒有了aa，ab列出之必要，但如此卻的確能在虛擬場數的狀態下舉出甲、乙二人較準確的獲勝機率，畢竟一場ax是可以抵掉兩個第二輪比賽的機率的。

學生認為不可行的有14份，達20.59％，其理由分別有：

      •aa，ab中a以經贏了，比下一場毫無意義。

    •因為每場單盤勝負機率不是甲贏，便是乙贏，單場勝負均等，必須看『總』結果是誰方先贏三場，『至多』來算的話，有可能錯估高了甲或錯估高了乙。

•因為ab是不可能發生的。

•aa，ab根本不須分開討論，只要先出現a就定勝負。可能結果應為：a，ba，bb，再用機率來思考。

    由問卷可知，許多學生檢驗其答案是正確的，所以，他們認為C之法是正確的，而部分學生認為其答案正確，卻無法接受其方法，原因在於『虛擬』的場數，但多數學生卻認為其『虛擬』之處，反而是絕妙之處。

關於問題4，學生認為不可行的有43份，達63.24％，其理由分別有：

    •這種方法有有將之前的結果和後續發展，兩人的機會相等等因素一起考量，所以可以阿。

      •他是依照兩人有可能贏的方法來漸漸推算，利用機率，公平。

    •因為此比賽應是機會均等，而兩人共分賭金，但由於甲對乙以先有2:1的領先優勢，縱使下一場的得勝機率均等，甲的得勝機率依然比乙高。但此法先將所有場錢數算出，先相加再除機率均等的2。

      •和期望值相類似，

，其中 ，就是甲先拿走的部分，

而 ，就是甲、乙兩人後來均分的錢。

學生認為不可行的有25份，達36.76％，其理由分別約有：

      •對乙不公平，在(2,2)的情況時，還可再比下去得 ，

所以，不應該以這種方式來方配。

      •D只考慮到下一場，沒考慮到下二場。

    •如果在甲：乙＝2:1時，再比一場，結果乙贏了，此時獎金應平分，如果先將96分給甲就不公平了，因為現在已經平手了，結果獎金卻不同。

    •我覺得題目在分時，就只考慮了這一次之機率，而未將之前的實際情況也納入考量。

    •那並沒有測出第五場的勝負，可能是甲或乙勝，若是乙勝，那甲「至少」得到的錢也會是0元。

      •此題所述皆屬片面、分段，沒有依『最後的可能結果』區分。

      •若今比一百局，而勝局比數1:0，不是要討論很久嗎?

由問卷得知，約有三分之一的學生認為D之方法不可行，其原因有二種，一是沒看清楚並了解D之方法，二是認為D只考慮了未來下一場的情況，而未考慮未來所有的情況。經過課堂上再一次探討欣賞D之方法後，大部分的學生發現其實D已經考慮了未來所有的情況，並且接受度大為提高。不過，洞悉到D之方法其實與他們所學數學期望值的概念類似者，卻是少之又少。

七、心得與建議

    筆者使用本工作單的時機，是在學生學習過機率及數學期望值後，其目的在檢視學生的對於相關觀念的理解。對於有心在一開始介紹機率時便引用此工作單的老師們，我們建議不可直接引用，應稍加更改內容才好。

    本工作單提供筆者一個省思，學生考試成績良好並非因為觀念正確。許多學生還未將觀念澄清，就開始做一大推題目。誠然，由做題目中去學習觀念，也許是學習數學的方法之一，但是，筆者卻總認為應該在更仔細推敲後，再以做題目的方式去練習運用觀念，這樣的學習才會穩固。在從學生的回答中，我們可以發現，他們對於所學過的「數學期望值」題目，幾乎都可以拿到滿分的評量，但是，為什麼可以這樣解題，能說得出其所以然之故的學生卻很少。我想，除了學生的學習方式或者有誤外，教師的教法也是重要的一個因素。由最後的結果得知，學生們並不認為筆者這份工作單的目的在於數學史，而是探討各種方式的可行性與否，並且從探討的過程當中，了解到機率的計算在於討論未來可能的情況以及機會的均等與否。這樣的結果，其實是筆者所希望成就的。

經過本次實驗，筆者了解到一位優良教師在教完觀念後，還要懂得如何多方面檢視學生的了解程度，幫助學生找到他們的認知盲點，才是最好的教學方法。筆者也將努力達此目標。

參考文獻

李文林主編 (1992)，《數學珍寶》，台北：九章出版社。

梁宗巨 (1995)，《數學歷史典故》，台北：九章出版社年。

陳敏皓 (2001)，〈古代數學文本在課堂上的使用—機率小史〉，《古代數學文本在課堂上 的使用》（國科會專題研究計畫成果報告，NSC 89-2511-S-003-031-; NSC 89-2511-S-003-121-），頁341-356。

Furingghetti, Fulvia and Domingo Paola (2003). “History as Crossroads of Mathematical  Culture and Educational Needs in the Classroom”, Mathematics in School. January: 37-42.

附錄：工作單

若有兩人各出資賭金96金幣，規定必須要贏三場者才能贏得全部賭金192金幣，但比賽中途因故終止，且此時勝局數(甲:乙)為（2:1），問此時應如何分配賭金？（甲乙兩人實力相當）

A認為，其賭金分配應就其勝局比數，即2:1，依比例分配，因此甲應分得 金幣，乙應分得 金幣。

問題1. 請問你認為A的分法可不可行？請說明 (可舉例)。

B認為，其賭金分配應考慮若不終止比賽，兩人各須贏幾場，按其各須贏得場數反比分配；即甲已贏2場，須再贏一場就可獲賭金，而乙已贏1場，須再贏二場就可獲賭金，因此甲所需場數：乙所需場數＝1:2，故其反比為 ，由此可知甲應分得 金幣，乙應分得 金幣。

問題2. 請問你認為B的分法可不可行？請說明 (可舉例)。

C認為，根據至多需要幾場比賽才能看出贏家，如果甲需要再比m場才贏；乙需要再比n場才贏，則需再經過m＋n－1場才能宣布贏家。以勝局比為（2:1）為例，接下來的二場比賽可能結果列出如下：

（a代表甲勝，b代表乙勝）

           aa           ab           ba          bb

         (甲勝)        (甲勝)       (甲勝)       (乙勝)

所以，兩人應該分的賭金比列為[3：1]，即甲可得 金幣，乙可得 金幣。

問題3. 請問你認為C的分法可不可行？請說明 (可舉例)。

D認為，甲贏兩局，乙贏一局，在擲下一次骰子時，若甲贏了，他將得到全部192枚金幣；若乙贏了，他們所贏局數比為2：2，在這種情況之下分賭金，每人將拿回自己的96枚金幣。縱上所述，若甲贏了將得192枚金幣，乙將獲得0金幣；若甲輸了則會拿到96枚金幣，乙會拿到96金幣，因此甲至少可拿到96枚金幣，乙至少可拿到0金幣。假如他們不繼續賭下去的話，可將96枚金幣先給甲，至於剩餘的96枚金幣，可能甲得，可能乙得，機會是均等的，所以甲乙兩人均分剩下的96枚金幣，各得48枚，因此甲乙兩人所得金幣各為[144；48]。

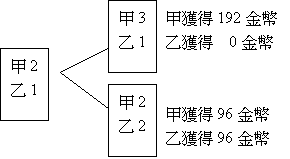因此，若今甲贏兩局，乙贏零局，中途停賽而分配賭金：

由上圖知，甲至少獲得144金幣，乙至少獲得0金幣，而剩下48金幣，可能甲得，可能乙得，機會是均等的，因此由兩人均分，所以甲得144＋24＝168金幣，乙得0＋24金幣。

問題4. 請問你認為D的分法可不可行？若不行，請說明 (可舉例)。

問題5. 利用你所學過的機率，此賭金分配問題應如何解？為什麼?