HPM隨筆（三）：2004勾股定理的『非常』遐想

台師大數學系 洪萬生教授

        近日內，阮錫琦（任教於台中市西苑中學）將他的兩篇新作寄給我欣賞，內容都與『勾股（定理）』有關，頗有藉以『連結』或『貫穿』相關高中數學知識之意趣。我想，在這開年之際，閒談兩則有關『勾股定理』相當個人化的一些遐想，聊供大家在春節假期上網之餘的談助，希望大家喜歡！

        其一、我們對於『勾股定理』或『畢氏定理』的證明方法，必須『精熟』到什麼程度才足夠？

        最近一年來的數學教育改革爭議中，有一個極為熱門的話題，就是數學的『精熟』度的標準之拉扯。譬如說吧，我們『做數學（計算）』(do mathematics) 究竟要多快、多準才行？說得比較『數學沙文主義』一點，我們的國民究竟要多精熟數學，才不會喪失所謂的『國家競爭力』？

        我在1985年九月剛進入美國紐約城市大學 (CUNY) 就讀沒多久，就在道本周 (Joseph W. Dauben) 教授的『自然科學史』通識課堂上，遭遇了『畢氏定理』的證明。我記得在那一堂課中，道本老師幾乎花了15分鐘，才把出自《幾何原本》的『面積證法』（參見圖一）講清楚。我當時相當震撼，因為我知道他在進入哈佛大學攻讀科學史學位之前，曾就學加州Claremont McKenna學院，最後以數學與英國文學雙主修之優異成績，榮獲雙學位。我至今還清楚記得，當時我『如坐針氈』，以致於『忍不住』走到黑板前，幫他畫好補助線並扼要講解。對我來說，不管是畢氏定理的哪一個證明，上述的『面積證法』也好，『弦圖證法』（圖二）也好，『比例證法』（圖三）也好，或者這些方法的組合乃至於再結合代數運算等等，都是充分『精熟』到如同『行雲流水』的程度了，因此，大概兩三分鐘（含當場畫圖）就可以搞定了。然而，道本老師這樣一位數學出身的著名數學史家，怎麼可能在這個『小 case』上磨蹭半天呢？

        我始終無以索解，也不好意思與他討論所以然之故–難道美國學者的數學『反應』都這麼慢嗎？後來，我與學長 David Rowe（德國Mainz大學數學史教授）見面，才解除了部分困惑。Rowe先從奧克拉荷馬大學獲得純數學博士學位，再轉到紐約城市大學來攻讀數學史 / 科學史博士學位，因此，我與他討論十九世紀的德國數學史（尤其是柏林、哥廷根學派），充分感受到他對數學之精熟與流暢。

        相對來看，道本老師的數學素養當然也沒有問題！其實，他在哈佛大學就讀期間，也被要求選修研究所層次的高等數學課程，這都可以解釋何以他研究起現代數學史人物如 Georg Cantor與Abraham Robinson時，根本沒有任何干格罣礙之處。只是或許因為他教授數學史與科學史，而不教授數學，所以，一直沒有機會演練譬如『畢氏定理』這樣的證明，以致於讓我覺得他的講解有笨拙之感。

        不過，我卻是到了過去這一年（將近20年之後）中，才能深刻體會道本老師當時『笨拙』的一種另類美感！對於他以及他的教育環境來說，既使在學院中主修數學，被期待的似乎也只是根本的理解就夠了，至於追求『精熟』所需時間，顯然被轉移到其他的『知識獵奇』上了，更何況他還需要主修英國文學呢。儘管如此，他仍然為自己保留了繼續深造成為『數學家』的可能性。他曾經告訴我說，學院畢業之後，他總共申請了五所大學的入學許可（與獎學金），其中除了哈佛大學科學史系之外，還包括普林斯頓大學哲學系，加州柏克萊大學，史丹佛大學，以及芝加哥大學等校數學系。最後，因為哈佛給他五年全額獎學金，他遂決定攻讀科學史博士學位，而成為世界知名的數學史家。

因此，道本老師的數學『笨拙』，恰足以襯托他作為一個數學史家 / 科學史家的全方位知識涵養！由此看來，既使是學界菁英（而且是數學史家 / 科學史家），犧牲一下數學『精熟』，這又何妨呢？這幾年來，本系相繼出現了好幾位文理兼備的優秀學生，他們目前正繼續深造中，最後都可能成為跨領域的菁英人才，因而有能力為台灣社會擎劃寬闊的願景。當我們『焦慮地吶喊』數學『精熟』之必要時，可曾進一步思考它的意義在哪裡呢，尤其針對這些跨領域的精英？

	圖一、取自徐光啟、利馬竇合譯的《幾何原本》

 

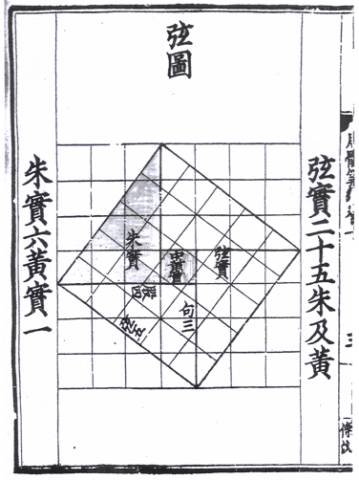
                        圖二、取自趙爽注《周髀算經》（1213年宋版）

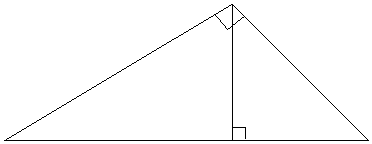
                                    圖三、比例證法

        其二、學習的評量點在哪裡？

        最近，我為了探討美國數學家如何介入數學教育，而有機會閱讀一些相關文獻，其中最能打動我的，莫過於由MAA (Mathematical Association of America) 所出版的《教師的數學教育》(The Mathematical Education of Teachers)。其中第5章的內容是有關

中學數學教師應該具備的素養 (recommendations for high school teacher preparation)。為此，編者利用了一個教學實例，以說明相關數學素養的重要性。在此一實例中，教師Liddell 小姐運用了改編自『弦圖』的一個問題 (task)：如圖四正方形邉長12，請問內嵌的正方形之面積為何？至於教學目標，則是希望學生利用畢氏定理求此內嵌正方形之邊長（為無理數），從而求得其面積。

        結果，有一位學生茱莉以圖五說明她的答案為80。不過，另一位學生比爾卻說：「我得到不同的答案，但是，現在看起來我沒有把圖畫對（見圖六）！我把每一邉分成3與9。」第三位學生亞麗莎 (Alicia) 接著說：「有沒有可能無論每邊怎麼分割，面積都會一樣？」Liddell小姐立即追問說：「妳怎麼想呢？如果這個點從分成4與8改變成為其他的分法，那麼，內嵌的正方形面積會保持一樣嗎？」

        當學生正在考慮那個問題時，他（她）們的老師也同時在思量琢磨。她必須盡快決定是否繼續她原先的教學計畫－連結此一問題與無理數，或者乾脆順著比爾的答案與Alicia的問題，把問題連結到代數等式：(a+b)²＝a²+2ab+b²，然後要求她的學生去核證這些內嵌的圖形都是正方形，或者利用圖形計算器探索這個『內嵌正方形面積函數』：y＝144－2(x)(12－x)。

        這樣一個『教學機緣』出現在課堂中，教師有沒有充分的素養決定如何繼續她（他）的教學活動，誠然是一個至關重要的問題。不過，如果欠缺類似上述的教學活動，那麼，我想有意義的問題大概也無從引出吧！因此，即使教師學富五車，如果從來不將學生視為學習主體，那麼，這些問題儘管在課堂中出現，大概也不會受到應有的對待！

        另一方面，如果視學生為學習主體，那麼，如何評量茱莉、比爾與亞麗莎等學生，對於教師而言，恐怕都是相當巨大的挑戰。因此，『評量點』究竟應該放在哪裡呢？是像茱莉一樣，回答了教師所期待的正確答案？還是像比爾『答非所問』但卻鬆動了原來『問題』(task) 的結構，而打開了寬闊的想像或思考空間？或是像亞麗莎馬上跟進而提出具體而有意義的新問題來？如果你（妳）是教師，他（她）們三人的平常分數要怎麼打呢？

        如果國、高中學校長或教師乃至於家長『各色人等』，很重視『統一』考試、『統一』閱卷的所謂『公平性』，那麼，或許身為老師的你，只好對比爾這樣的學生說一聲抱歉了！至於會不會因此而扼殺了一位學生的想像力或學習興趣，乃至於降低了所謂的『國家競爭力』，當老師的一切『秉公』行事，當然可以『姿態優雅地』走開了。

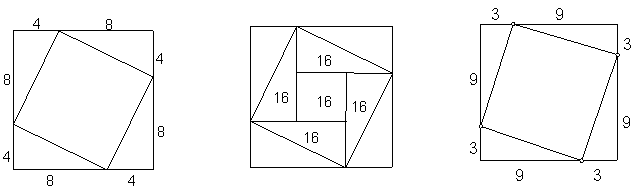
              圖四                                                                      圖五                                               圖六

參考文獻

洪萬生 (2004).〈美國數學家如何介入數學教育？〉，《科學月刊》第35卷第2期。

阮錫琦 (待刊稿).〈幾何學中的魔法棒－『畢氏定理』〉。

阮錫琦 (待刊稿).〈『HPM』的重要性〉。

CBMS (2001). The Mathematical Education of Teachers. http://www.maa.org/cbms.