『盈不足術』與老鼠穿牆的「恩怨情仇」

台師大數學系碩士班研究生 張復凱

《九章算術》第七卷『盈不足』，共有二十個問題。其中，前八題是在處理『純粹盈不足』的問題：第一到第四題是『有盈、有不足』的情形；第五、六兩題分別是『兩盈』及『兩不足』；第七、八兩題則各是『不足、適足』及『盈、適足』的情形。

以第一題為例：

今有共買物，人出八，盈三；人出七，不足四。問人數、物價各幾何？

《九章算術》提出的解題方法，亦即『盈不足術』：

盈不足術曰：置所出率，盈、不足各居其下。令維乘所出率，并以為實。并盈、不足為法。實如法而一。盈不足相與同其買物者，置所出率，以少減多，餘，以約法、實。實為物價，法為人數。

若運用現代數學術語表達，則上述問題可以翻譯成為：『若是每人出 ，則多出了 ；若是每人出 ，則不足 。問人數 、物價 各多少？』至於解法則如下：每人出錢 ，人數 ，物價 。以第一題為例，即為每人出錢  ，人數 ，物價 。前四題皆以『盈不足術』解決，至於第五到第八題，方法亦類似。

有趣的，是《九章算術》在處理完八題基本的盈不足問題後，便將「每人出錢 」這部分中「 」的解題方式（後有詳述），運用到一般表面上非盈不足型的問題上。如第十二題：

今有醇酒一斗，直錢五十；行酒一斗，直錢一十。今將錢三十，得酒二斗。問醇、行酒各得幾何？

《九章算術》採用的方法是：

假令醇酒五升，行酒一斗五升，有餘一十；令之醇酒二升，行酒一斗八，不足二。

再用『盈不足術』中的『 』解題，得醇酒 升。

這樣的解題方式，後來在歐洲被稱為「雙設法」(rule of double false position)。像是意大利數學家斐波那契 (Fibonacci, 1170?~1250) 所著《計算書》(Liber Abaci, 1202，亦譯作《算經》) 第十三章介紹阿拉伯人的Elchayam法（即「雙設法」），便是在討論這類問題。洪萬生在〈十三世紀西歐數學百科全書：斐波那契的《計算書》〉一文中，更指出此章的題型非常類似《九章算術》中的〈盈不足術〉，像是先前所提的『兩盈』、『兩不足』、以及『一盈一不足』等三種情況，也都在《計算書》中出現。至於《九章算術》與《計算書》兩者間的關連，則是眾說紛紜。不論如何，這種方法，就像錢寶琮所言：「在十六、七世紀時期，歐洲人的代數還沒有發到充分利用符號的階段，這種萬能的算法便長期統治了他們的數學王國。」¹足見其重要性。

不過，必須注意，以『盈不足術』解一般的問題時，只有在處理一元一次方程式的問題，才可求出正確解。以現代數學術語說明：若要解決Ax=B這個一元一次方程式時，先用 與 代入x處，在比較方程式等號左邊的A 、A 與右邊的B後，發現分別多出 與不足 ，即 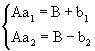。於是我們可以解出 ，這也等同於原式Ax=B導出 的解。但是，很明顯地，一旦面對非一元一次方程式時，這種方式求出的解，就可能只是近似解。

以盈不足第二十題為例：²

今有垣厚五尺，兩鼠對穿。大鼠日一尺，小鼠亦日一尺。大鼠日自倍，小鼠日自半。問幾何日相逢？各穿幾何？

答曰：二日一十七分日之二

術曰：假令二日，不足五寸；令之三日，有餘三尺七寸半。

即以盈不足術求得日數 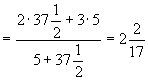日。

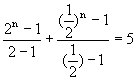由於本題的兩隻老鼠分別以公比為2和 的等比級數穿牆，以現在的表示法為 ，並非一元一次方程式。所以，求出的 明顯地與利用『盈不足術』所算出的 不同。因此，這個問題被認為只能求出近似解而非正確解。另外，還有第十一題「蒲與莞」出現等比級數、第十八題「良馬與駑馬」出現等差級數，都因類似的情形而同樣被視為僅能求出近似解。

當一般中算史家認為《九章算術》的作者沒有正確地解決這三個問題時，³沈康身在他的《九章算術導讀》中，則為此平反。沈康身認為，等比級數和等差級數都是在項數是正整數時才有效，所以，像第二十題的 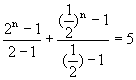指數方程式以連續量的方式求出 是無意義的。他認為，正確的情形應該是：
大鼠穿洞速率為 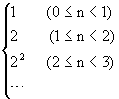，小鼠穿洞速率為
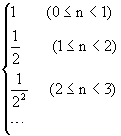
所以大鼠穿洞距離為 ，
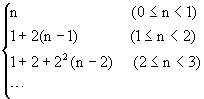小鼠穿洞距離為
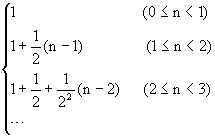
因為兩鼠會在 時相遇，所以，可以列出方程式 ，並解得 。也因為這是一元一次方程式，對照前面所提，《九章算術》的『盈不足術』同樣也求出 。沈康身認為 才是正解，亦即《九章算術》的答案並非近似值，而是正確值。

同樣地，本書第十一題和第十八題也可利用相同的方式來解讀，而認定所求為正確值而非近似值。

對此，莫紹揆亦指出：「在盈不足章中有三例用到階梯函數，未受到人們認可，遂致以為算法有誤，或只得近似解。」⁴呼應了沈康身的看法。

那麼，究竟一般中算史家所認定的近似解與沈康身和莫紹揆認為的正確解孰是孰非？

先丟開各種「算」法，重新檢視這些題目。藉由貼近這些問題的本意，以確認何者較為合理。

回到第二十題。大鼠的穿洞速率變化情形，在兩種解讀下，分別為：

1.              近似解的角度下，大鼠的穿洞速率為 。（n為天數）

2.              正確解的角度下，大鼠每天都以固定的速率穿洞。第一天速率恆為1、第二天速率恆為2……

在我看來，「 」的速率，怎麼看都覺得彆扭。相對而言，把穿洞速率視為等速率，顯得自然多了！是故，『盈不足』卷中第十一、十八、二十題的解應非近似解，而是「道道地地」的正確解。

這樣的結論，必定給那些總相信主流想法而欠缺省思的書呆子，大大地震撼教育一番，讓我們警覺到『盡信書不如無書』的真理。此外，也提醒我們解決問題時，必先貼近問題的脈絡。對於史學的研究，更是忌諱把古代的問題，丟到現代的脈絡之中。這種務必貼近脈絡的警惕，對我來說，或許是比發現正確解的結論更為重要吧！（小小開個玩笑，那《九章算術》的作者有沒有搞清楚老鼠們鑽牆時的脈絡？）

最後，還有一件事令我感到困惑。以第二十題為例，雖然老鼠穿牆每天都是等速率，但因為隔一天速率就會變化，所以，『盈不足』的方式只有在盈與不足的鄰界處才會適用（另外兩題也是如此）。亦即：若原文中「術曰：假令二日，不足五寸；令之三日，有餘三尺七寸半」改為「假令一日，不足三寸；令之三日，有餘三尺七寸半」，答案就會變成 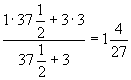，和正解的 可是天差地遠囉！

那麼，究竟《九章算術》的作者是否有意識到這樣的情形，或只是碰巧算出正解。我想，『盈不足術』與老鼠穿牆的「恩怨情仇」看來是沒完沒了啦！

註解：

1.      錢寶琮《中國數學史話》，盈不足術。

2.      本文盈不足問題題號採郭書春與劉鈍點校的《算經十書》編排方式。孔刻本將此題移至十二題，而之後題目順移一位。

3.      郭書春《古代世界數學泰斗劉徽》、劉鈍《大哉言數》、李繼閔《九章算術及其劉徽注研究》都持此觀點。

4.      本敘述引自沈康身所著《九章算術導讀》。

參考資料：

洪萬生 (2003).〈十三世紀的西歐數學百科全書：斐波那契的《計算書》〉，《科學 月刊》34 (7): 636-642.

郭書春、劉鈍 (2001).《算經十書》，台北：九章出版社。

李文林 (2000).《數學珍寶》，台北：九章出版社。

沈康身 (1997).《九章算術導讀》，漢口：湖北教育出版社。

郭書春 (1995).《古代世界數學泰斗劉徽》，台北：明文書局股份有限公司。

劉鈍 (1995).《大哉言數》，瀋陽：遼寧教育出版社。

李繼閔 (1992).《〈九章算術〉及其劉徽注研究》，台北：九章出版社。

錢寶琮 (1957).《中國數學史話》，北京：中國青年出版社。