曲線下面積學習單的設計

西松高中 蘇惠玉老師

一、前言

在現行高三數學課程中，下學期為微積分的部分；分成兩章，一章為極限的概念，另一章為極限的應用。其中有關於積分的部分，只在最後一小節中利用「分割與逼近」的方法，求曲線下的面積，以利學生大學後進一步學習定積分。由於在此節之前，都是有關於微分的應用，所以，在此節開始前，在引起動機方面，教師必須舉一些「例子」，說明此節的基本觀念，即利用分割與逼近的方法，可以求出曲線下的面積。

在龍騰版教科書中，書上舉出的例子為折線形下的面積，利用「分割」算出總面積；在此只點出「求面積利用分割的方式」，而忽略的了直線形與曲線形的最大不同點，就在誤差的處理。而南一版的教科書中，利用葉子來估計面積，引出分割與逼近的概念。在南一版的教師手冊中，此節的「教學活動策略」中的「布題活動」，是教師將紙撕成不規則形狀，再將圖形描繪於黑板上，讓學生思考如何算出面積。這些活動雖然切合主題，但是感覺像國中生的「教學活動」，可能高三的學生會覺得有點小幼稚。

在這一節的教學活動中，我希望能有些例子，讓學生看出不同分割的方法，逼近的重要性及困難之處，以及數學家在面對困難時採取的策略，進而加強學生對「分割與逼近」基本概念的瞭解。

二、教學省思

        這個單元放在三年級下學期最後一個單元，為「極限的應用」中的一節，用意在於讓學生知道如何利用「分割與逼近」的極限應用，得到曲線下的面積。教科書的教材的重點，或是目標，在於讓學生「了解」利用極限的方式，就可以得到曲線下的面積。雖然「分割與逼近」在現在的學生看來，似乎理所當然，但是，數學家幾百年來面對同樣問題時的困境、苦思的解決之道，學生似乎完全不能體會！所以，我想要設計一份學習單，讓學生對分割的方法，有較為寬廣的視野，同時了解分割完後，數學家面對的困境，以及不同的文化、時空背景之下，採取的解決路徑的不同。讓學生在學習積分的啟蒙觀念時，同時學會「欣賞」與分析不同的數學證明方式。

三、史料分析

        這份學習單，我選擇的史料有劉徽的割圓術、阿基米德圓面積的證明、克卜勒對阿基米德圓面積公式的證明、以及阿基米德拋物線弓形面積的證明。劉徽與阿基米德的圓面積公式都是「半周半徑相乘」，證明過程中，也都有提到利用圓內接與外切多邊形，但是證明策略卻是大異其趣。

我們以時空背景來看，劉徽是魏晉時候人。魏陳留王景元四年（公元263年）撰《九章算術注》，當時劉徽約30歲左右。劉徽受到什麼學說、什麼人的影響，而提出如「割圓術」的想法不得而知，但是，我們卻可在中國史上哲學思潮最興盛的春秋戰國時期，在墨子的《墨子》卷十的《經上》、《經下》、《經說上》、《經說下》中，發現劉徽為何作如是想的蛛絲馬跡。

就無窮大而言，《經上》寫道：「窮，域有前不容尺也」，《經說上》：「窮，不容尺有窮，莫不容尺無窮也」，亦即用尺來度量路程，如果量到前面只剩下不到一尺的剩餘，則這段路程是有窮的；如果繼續量下去，前面總有超過一尺，那麼，此路程是「無窮的」。1鄒大海認為，這是用一個度量單位來界定有窮與無窮，在承認「無窮大」存在的前提下探討其本質，這點與希臘傳統下對「無窮」採取迴避的態度截然不同。

就無窮小與分割的部分，

《經上》：                                             《經說上》：

「端，體之無厚而最前者也。」      「端，無間也」

「久，彌異時也。宇，彌異所也」  「久，古今旦莫。宇，東西家南北」

「始，當時也」                           「始，時或有久，或無久。始當無久」

此處的「厚」，可作「厚度」或是「量的多少」來解釋。2同樣的，「時」有「期間」和「瞬間」二義。「始」為久之最初的瞬息，所以當無久之時。「端」和「始」都是度量為零，但不是「無」。由此再來看《經下》與《經說下》的分割概念，《經下》：「非半弗 ，則不動，說在端。」《經說下》：「非， 半進前取也，前則中無為半，猶端也。前後取則端中也。 必半，毋與非半，不可 也。」 ，破也，有分割的意思。意即每次中分一體，最後必有一不可分割的「端」。劉徽在其注中所言：「割之彌細，所失彌少。割之又割，以至於不可割，則與圓周合體而無所失矣。」由此似乎可以看出墨子學說對其影響。

但是阿基米德還在當時的希臘文化傳統的影響之下，深受季諾悖論之苦（請參考筆者另一篇文章，〈從一個問題說起：無窮〉，刊登在《HPM通訊》第五卷第一期）。所以他只好採取迂迴戰術，以兩次歸謬的方法，間接證明圓面積公式。但是，到克卜勒在寫《測量酒桶的新立體幾何》(1615)時，他似乎不受這樣的傳統所影響，大膽的說「圓的周長可以分成如同點一樣多的部分，亦即無窮多個(infinite number)部分」。或許克卜勒只是覺得這樣方便行事吧！

四、學習單的設計理念

        我的目標是找一些例子讓學生有學習動機，並且作為從直線形轉換到曲線的引子，同時讓學生了解分割的方法與求面積所面臨的困境，及不同的解決方法。由於這份學習單預計在三年級下學期四月時實施，此時學生的心理上，較不希望老師在課程已經上不完的情況下，再作些與課本教材內容無關的教學活動，所以我在選擇史料與問題設計上，盡量與學生所學與將學的「數學知識」有關。學習單中將涉及的證明過程列出，為學生了解、學習的重點；再以問題引導的方式，讓學生進一步反思在證明過程中所透露出的數學知識邏輯上的意涵、文化背景上的意義。希望學生透過此份學習單，能引起學習動機，對「積分」的概念有進一步的理解與體會。以下為學習單的完整內容：

　

Card 1：劉徽之割圓術

《九章算術》卷一 方田

又有圓田，周一百八十一步，徑六時步三分步之一。問為田幾何？

術曰：半周半徑相乘得積步。按：半周為從，半徑為廣，故廣從相乘為積步也。假令圓徑二尺，圓中容六觚之一面，與圓徑之半，其數均等，合徑率一而弧周率三也。

(C=6•r, r=1)3

又按：為圖。以六觚之一面乘一弧半徑，三之，得十二觚之冪。

( )

若又割之，次以十二觚之一面乘一弧之半徑，六之，則得二十四觚之冪。

( )

割之彌細，所失彌少。割之又割，以至於不可割，則與圓周合體而無所失矣。

觚面之外，猶有餘徑，以面乘餘徑，則冪出弧表。

( >圓面積)

若夫觚之細者，與圓合體，則表無餘徑。表無餘徑，則冪不外出矣。

( ， ，An<圓面積< ， ＝圓面積)

以一面乘半徑，觚而裁之，每輒自倍。故以半周乘半徑而為圓冪。

(圓面積＝ ，a×r=2A，圓面積＝ )

此以周、徑，謂至然之數，非周三徑一之率也。

 

      

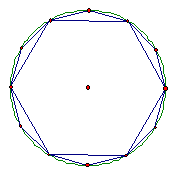
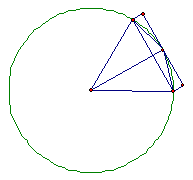
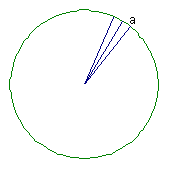
設an=6×2n邊形的邊長，An=6×2n邊形的面積，Sn==6×2n邊形的周長。

問題：

1.      試證明： 。

2.      試證明： 。

3.      在上述的文字中，你覺得哪段話具有「極限」的概念？

4.      你覺得在劉徽證明圓面積公式的過程中，有哪些邏輯上或是「感覺上」不嚴密，或有問題的地方？

5.      為何此時的圓面積公式為 ，而不是 之形式？這兩形式的寫法，有何差別？

Card 2：阿基米德圓面積公式之證明

《圓的度量(Measurement of a Circle)》

命題1：任一圓的面積等於以該圓的半徑和周長為兩直角邊的直角三角形的面積。

設ABCD是給定的圓，K是所述的三角形。

如果圓面積不等於K，那麼它一定大於或小於K。

 

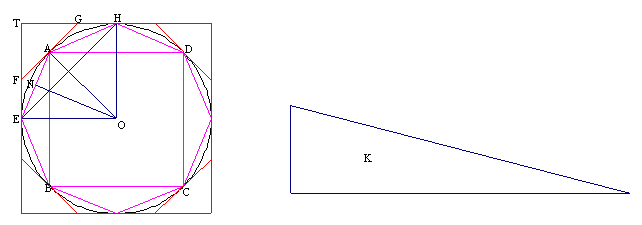
I. 如果可能，設圓面積大於K。

作圓的內接正方形ABCD，平分弧AB、BC、CD、DA，然後等分其半（如有必要），繼續分下去，直到以分點為頂點的內接多邊形各邊所對弓形面積之和小於圓面積與K之差。

弓形和＝圓－內接多邊形<圓－K

這樣，多邊形面積大於K。

設AE為多邊形的任一邊，ON為引自圓O垂直於AE的垂線。

那麼ON小於圓的半徑，因而小於K的一直角邊。又多邊形的周長小於圓周長，即小於K的另一直角邊。

多邊形＝ <K

所以多邊形面積小於K，這與前面假設矛盾。

故圓面積不大於K。

II. 設圓面積小於K。

作圓的外切正方形，設該正方形與圓切於E、H的兩鄰邊交於T。平分相鄰兩切點間的弧，並在分點處作切線。設A為弧EH的中點，FAG為A的切線。

那麼角TAG為直角。因而有

TG >GA

>GH，

由此可得，三角形FTG的面積大於TEAH面積之半。

類似地，如果平分弧AH，並作分點處的切線，那麼，在GAH內，該切線將截出一個三角形，其面積大於GAH的一半。

如果繼續這種作法，最後可得到一外切多邊形，使得該多邊形與圓所夾圖形的面積小於K與圓面積之差。

(1/2)弧形＝外切多邊形－圓<K－圓

由此之，多邊形的面積小於K。

因為引自O垂直於多邊形任一邊的垂線等於圓的半徑，而多邊形的周長大於圓周長，由此可得，多邊形的面積大於三角形面積K，這是不可能的。

外切多邊形＝ ＝K

因此圓面積不小於K。

由於圓面積既不大於K，也不小於K，所以二者相等。

問題：

1.      在I.的證明中，哪些文字有「極限」（或無窮）的概念？

2.      在II.的證明中，哪些文字有「極限」（或無窮）的概念？

3.      在阿基米德的證明過程中，你覺得有無邏輯不嚴密的地方？若有，是哪一部份？

4.      比較劉徽與阿基米德的證法，你覺得有何差異？為何會有這樣的差異？

5.      你覺得劉徽與阿基米德的證法哪一種較好？為什麼？

 

Card 3：克卜勒為阿基米德圓面積公式的證明

《測量酒桶的新立體幾何》

第一部份：規則圖形的體積

定理二：圓面積和以其直徑為邊的正方形面積之比為11: 14。

阿基米德用間接證明得到了如果面積超過了這個比例，那它就太大了。這就如同這個意思。見圖。

圓BG的周長可以分成如同點一樣多的部分，亦即無窮多個(infinite number)部分，每部分可看作一個等腰三角形的底，該三角形有等腰AB，所以，在圓面上有無窮多個以A為公共頂點的小三角形。現將圓BG的圓周拉直到直線BC，且使BC等於圓周長。這無窮多個三角形或扇形的底則假設會(supposed to be)一個挨一個地落在直線BC上。假設BF是這些底中的一個，CE是等於它的另一個。接連FA、EA、CA，則生成三角形BAF和EAC。顯然，BC上的這種三角形的數目同圓上的扇形數目一樣多。且底BF和EC相等，而所有三角形的高都是BA（BA也是扇形的高），所以三角形BAF與三角形EAC面積相等，且等於每一個扇形。因為各三角形的底都在BC上，所以三角形BAC，由所有這些三角形所組成，會等於圓內所有扇形，所以等於圓面積（該圓是由這些扇形所組成的）。這等價於阿基米德通過歸謬法得到的結論。

問題：

1.      你覺得克卜勒對圓面積的分割想法，與阿基米德相同嗎？若不同，不同之處在哪？

2. 你覺得克卜勒對圓面積的分割想法，較接近劉徽或是阿基米德的想法？為什麼？

3.      你覺得哪一種證明較「嚴密」？

4.      你覺得哪一種較有課堂上所學過的「微積分」的概念？

5.      猜想一下，克卜勒如何利用圓面積的證明形式去測量酒桶的體積？

Card 4：阿基米德拋物線面積

《拋物線圖形求積法(Quadrature of the parabola)》

命題23：給一序列的面積A, B, , D, …, Z，其中A為最大的一個， 且每個等於下一個的4倍，則 

取面積b, c, d,…使得b= B, c= C, d= D等等；

則因為b= B，B＝ A，所以B+b＝ A，同理C+c= B，…，所以

B+C+D+…+Z+b+c+d+…+z= (A+B+C+…+Y)

但是 b+c+d+…+y= (B+C+D+…+Y)

所以，藉由減法，

B+C+D+…+Z+z= A，或是

A+B+C+…+Z+ Z= A。

命題24：每一個由拋物線和弦Qq所圍成的弓形(segment)等於與此弓形同底等高的三角形的 。

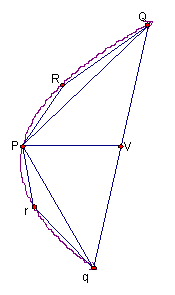假設 ，其中P為弓形的頂點1；則我們必須證明弓形的面積等於K。

因為，如果弓形的面積不等於K，它必須是大於或是小於。

I. 假設弓形的面積大於K。

如果我們分別在由PQ，Pq所截的弓形中，作與弓形同底等高的內接三角形，亦即此兩三角形與兩弓形有相同的頂點R, r，如果我們在剩餘的弓形中，以相同的方式內接三角形，如此一直繼續，直到剩下的弓形面積之和小於弓形面積與K之差。

剩下弓形＝弓形－多邊形<弓形－K

所以，如此形成的多邊形必須大於面積K，這是不可能的，因為[命題23]

A+B+C+…+Z< A，其中，A＝

B＝△PRQ＋△Prq＝1/4 △PQq

所以，弓形的面積不可能大於K。

II. 假設，如果可能，弓形的面積小於K。

則如果 =A，B= A，C＝ B，如此下去，直到我們得到一個面積X，使得X小於K與弓形面積的差。我們可以得到，

A+B+C+…+X+ X= A=K

現在，因為K超過A+B+C+…+X一個小於X的面積，且超過弓形的面積一個大於X的面積，

K－(A+B+C+…+X)<X，

K－弓形面積>X

所以，A+B+C+…+X>（弓形面積）

因為命題222，這是不可能的。因此，弓形的面積不小於K。

所以，因為弓形的面積不大於也不小於K，所以

(弓形PQq的面積)=

 註：

1.      若Qq為拋物線弓形的一底，且V為Qq的中點，如果過V的直徑交曲線於P，則P稱為此弓形的頂點。

2.      命題22為如果有一序列的面積A, B, C, D,…，每一個是下一個的4倍，且如果最大的那一個，A，等於內接於拋物線弓形PQq的三角形PQq，且與弓形同底等高，則

(A+B+C+D+…)<(弓形PQq的面積)。

問題：

1.      將命題23的 寫成等比級數公式的形式。

2.      如右圖，如果Qq是被直徑PV平分於V的拋物線的弦，直徑RM於M點平分QV，RM是從R到PV的縱（坐）標，證明：PV＝ RM。（命題19）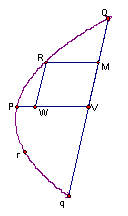

　

　

　

　

　

3.      證明：如果任一拋物線弓形的底為Qq，頂點為P，R是由PQ所截得的弓形的頂點，則 。(命題21)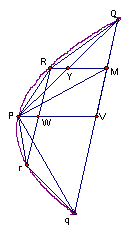

 

 

 

 

 

五、實施與建議

        此份學習單重點在於證明過程，所以以講述的方式實施，讓學生覺得跟平時上課的內容較為接近，再以提問的方式，讓學生回答學習單中的問題。在「曲線下的面積」這一單元上課之前實施，時間為兩節課。然後再完整上完「曲線下的面積」這一單元後，讓學生作一回饋問卷，以評估學生在此份學習單的學習成效。回饋問卷的問題如下：

「曲線面積學習單」回饋問卷

1.      你覺得這幾張「曲線面積學習單」對你學習「2-5 曲線下的面積」單元時，有沒有幫助？

□ 有（請續達第二題）     □ 沒有（請寫上原因）

2.      你覺得是在哪一方面對你的學習有幫助？（可以複選）

   □ 學習動機    □ 「如何求曲線下面積」的觀念更清楚    □ 「積分」的觀念更清楚
   □ 證明方法的了解    □ 中西文化的差異    □ 歷史故事、趣聞  
   □ 考試成績的提升    □ 數學能力的提升

回收問卷63份，只有3份填上沒有幫助，原因為聽不懂、考試不會考。其餘皆認為有幫助，其中「學習動機」佔35%，「「如何求曲線下面積」的觀念更清楚」佔49%，「「積分」的觀念更清楚」佔35%，「證明方法的了解」佔58%，「中西文化的差異」佔60%，「歷史故事、趣聞」佔67%，「數學能力的提升」佔25%，其中只有一位同學填「考試能力提升」。

或許這次回饋問卷的設計並不理想，畢竟是以「引導」的方式，讓學生選擇選項。因為我覺得以前開放式的讓學生回答覺得有哪些幫助時，學生的回答通常只有一點，但是學生「學習」、獲得的部分卻應該是多元的，所以我才以選擇的方式讓學生自己勾選，或許以後會有更好的問卷設計方式吧。在學生的回饋中，可以發現「歷史故事、趣聞」仍佔多數，想要以有趣的方式，將人類文化中的數學創作融入到數學教材中，這似乎是不可避免的。總之，此份學習單內容雖然不多，但從學生的回饋來看，似乎已經達到當初設計的目標了。

 

註解：

1.      參考錢寶琮《中國數學史》。

2.      參考鄒大海，〈《墨經》中的無限思想〉。

3.      此張學習單括號中的式子為解釋劉徽文字的內容。

參考文獻

Calinger, R. ed. (1995). Classics of Mathematics. New Jersey: Prentice-Hall, Inc.

Heath, T.L. ed. (2002). The Works of Archimedes. N. Y: Dover Publications.

李文林主編 (2000).《數學珍寶》，台北：九章出版社。

錢寶琮 (1932/1998).《中國算學史》（上篇），收錄於《李儼錢寶琮科學史全集》第一冊。瀋陽：遼寧教育出版社。

錢寶琮主編 (1992).《中國數學史》，北京：科學出版社。

郭書春 (1995).《中國古代數學泰斗劉徽》，台北：明文書局。

鄒大海 (1992).〈《墨經》中的無限思想〉。

蘇俊鴻 (1999).〈兩個證明的比較〉，《HPM通訊》第二卷第十二期。