最美的數學式

『美，是首要的標準；醜陋的數學在世界上是找不到永久藏身處的！』---G. H. Hardy

台灣師大數學系助教 謝佳叡

        美，絕對是數學的特質之一。當一個定理顯的醜陋時，某種程度也暗示著：有一更好的證明等著被發掘！前一陣子，偶拾一書，書名為《最美的數學公式（The Most Beautiful of Mathematical Formulas）》，作者L. Salem、F. Testard 及G. Salem 在序言裡開宗明義的闡述：『本書的目的在於揭示數學公式之美！』全書分成十大類，介紹約四十個數學公式、數學名詞的緣起、例證、多方面的應用及相關歷史發展，除了讓讀者品嚐這些公式、名詞發展的趣味外，也呈現符號化後數學公式的美。然而，作者卻未對『為何選擇這些公式』加以說明。這勾起筆者的好奇心，正值2000年總統大選，心想---何不來個『數學式子票選活動』？

貳、實施說明：

        決定將這個想法付諸行動時，首先必須面對的，就是問卷的設計和實施方式，包含：（一）應採用選擇式或是開放式的票選方式？（二）如何設計問題？（三）受測樣本如何選擇？（四）如何分析調查結果？而這些問題彼此亦相互關連，越去考慮就越難以著手進行。幾經思考後得到了一個結論：『又不是要當成嚴肅的研究報告，而且無論結果如何，都不會影響這些式子的地位與價值，何不放開心胸，Just for fun！』

一有這個念頭，這些問題就顯得容易著手了。

1. 票選方式決定採用事先提供選項，除了為了方便統計外（有點私心），也可減輕填寫者的困擾（不必再去思考、回憶有哪些數學式子而減低填寫意願）。當然了，受呈現式子的干擾是無法避免的，使得寫出的式子可能並非心目中真正的答案，這也使得『要列哪些選項？』成了這份問卷必須面對、也是最困擾的問題。數學公式成千上萬，加上定義、定理、等式……真如夜空繁星一般，不可勝數。為解決此一問題，本問卷的選項選定原則如下：
1. 儘量以符號呈現，捨棄文字的敘述與過於冗長的式子。
2. 型式簡單，一覽即知。
3. 不要列上同質性過高的式子，但容許各有特殊意義者或形式差異過大者。

實際的作法是由《最美的數學公式》一書中挑出15個符合上述者，再由筆者參考手邊書籍另行補列14個，合計29個。另留有空欄供填寫者自填，以彌補選擇式的方法所造成之不足。不可諱言地，如此的選項設計，設計者個人偏好之融入是無法避免的，而且從許多面向來看，這樣子的選項設計仍顯粗糙（例如不少受試者反應選項的同質性還是過高，如選項17和18本係同源、選項10是選項6畢氏定理的變型、三角公式選項過多、沒有向量公式等等），這些都是筆者當初未料及的（或說是能力不足）。不過也無妨，當成拋磚引玉之用也是本文的另一個目的。

2. 本問卷共有三個問題，每個問題至多填寫5個選項，不分順序，問題如下：
1. 你覺得最美的數學式子是哪些？
2. 你認為最有用的數學式子是哪些？
3. 你最想知道哪些數學式子的發展史？

當然，所謂『美』、『有用』的定義是因人而異，本問卷並未說明，由填寫者自行解讀；而第三題設計的目的，除了提供『HPM』的編輯小組作為參考外，也反映出填寫問卷者的需求與不足的面向。

3. 本次問卷對象為台灣師大數學系大學部一至四年級學生，每年級約100人，另有研究生40人。
4. 分析方式採『量』的統計，將三個問題的調查結果，分年級依得票數的高低呈現前十名排行，並統計大學部的總排行；最後一欄為研究生調查結果，因為該組調查人數較少，故排行不定取足十名。必須強調的是這裡所謂的『排行』，也單純針對台灣師大學生對這些式子的看法，絕無區別數學式子優劣之意，所列數學式每個皆是一部歷史，都是人類智慧的結晶，豈是吾等足以撼之。

由於選項設計、取樣對象皆是偏隅之選，統計人數也仍算少量，加上本文篇幅關係及個人能力有限，對於結果在此僅做一些現象的描述，不做詳細的分析探討，至於如何解讀數據背後的意義，就交由有興趣的讀者了。

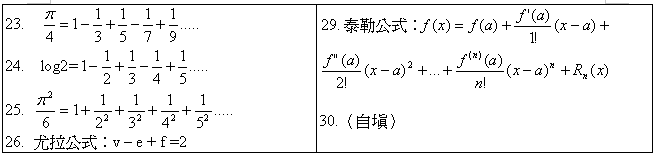
參、選項：

   

   

    （＊）現在所說的質數定理型式為： ，本問卷直接採用《最美的數學公式》書上的型式，特此說明。此式更精確的表示法為：

第n個質數

     （資料來源：Paulo Ribenboim所著《The little book of big primes》(Springer-Verlag 1991) p.141）

肆、統計結果：

    不妨找找看，你能發現什麼！

（一）大學部由泰勒公式與畢氏定理拔得頭籌，研究生則由尤拉公式奪魁。

（二）Fibonacci數列受歡迎的程度隨年級而降低；尤拉公式卻相反，這大概和大二有幾何課程有關。

（三）研究所高排行的級數式子，顯然還未被大學部所欣賞。

（四）票數最低的：大學部是 （3%）；研究所也是選項11.12.13的三角公式（0％）。

（五）值得一提的是，『十進位』也被列入自填部分，獲得了不少票數；此外餘弦定理、 也在自填的項目中出現。

（一）畢氏定理一路奪魁，泰勒公式緊追在後。而且除了這兩個也在『最美』的部分上榜外，其餘大都消失了，這說明了『美』和『有用』不一定相伴而行。

（二）上榜者除了泰勒公式外，其餘都在中學時就學到這些公式。

（三）總得票數最低的，是選項23.24.25.的級數公式（0％），以及27的質數定理（0％）。

（一）雖然泰勒公式和尤拉公式佔據了高排行，質數定理也居高不下，但在大二，泰勒公式卻不見了，取而代之的是Fibonacci數列居於榜首，頗耐人尋味。

（二）畢氏定理在大三以上就消失在榜上，或許與大三的教育課程學生必須時常接觸有關。

（三）大四的圓球體積公式突然竄起（不知是否與校外試教或數學史課程有關）。

（四）總得票數最低的，又落在選項11.12.13的三角公式（0％）。看來這個普遍為學生夢魘的三角函數公式，即使在數學系仍心有餘悸吧！

伍、相關資料比較：

   David Wells 在1988年，針對《The mathematical Intelligencer》的讀者（vol.10 No.4 p.30）也曾做過類似的調查。相同的，Wells也事先給了讀者24個選項，因為該雜誌的讀者群大都為專業數學家，故選項的設計就更加的深廣，形式也更多樣（包含定理與性質的敘述都在選項之列），回收的問卷也以數學家為主，被認為最美的前十名為：

後記：

        當時，一股衝動的做了這樣的一個調查，由於事先並未請教過一些先進的意見，許多很好的建議與指教都在調查實施之後才獲得，甚感可惜。為忠於原始調查資料，故所呈現的設計儘管粗糙也未加以更動。也期待有更完善的調查產生，或許也可來個『數學家票選』、『數學定理票選』活動，相信一定十分有趣。