為什麼是阿基米德開平方法？

西松高中 蘇惠玉老師

高中理科下冊〈1-3 平方根的近似值〉中提到：阿基米德在求圓周率需要開平方，用到的是下列的不等式：

辦公室的同仁問我：阿基米德是在什麼樣的情形使用的？

        事實上，阿基米德只給出 的近似值：

他並沒有做任何的解釋，說明這些近似值是怎麼得到的。惠爾慈（Hultsch）利用與希臘幾何學家同樣的分析方法，來說明阿基米德應該是如何得到這樣的近似值的。若將這兩個近似值分析及變化一下，就可以知道其關連性。 ，而 ，所以可得

而這等價於

但是，

因此，惠爾慈仿照希臘方式，可得到這一不等式： 。T. L. Heath認為，毫無疑問地，阿基米德實際上也發現並證明了同樣的結論。他認為下列的事實確定了這個假設的可能性：

(1)       海龍(Heron，公元1世紀)的某些近似值說明，他知道並且經常用公式 。

(2)       阿拉伯人阿爾卡西（Alkarkhi，公元11世紀）吸收了希臘原始原始資料之後，使用了公式

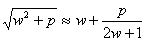
事實上，在更早的巴比倫人找平方根的近似值時，就已經用到了這樣的式子了。例如找 的近似值時，因為4比 小，而 ，所以 應該比 大。因此， 。而在目前所知中國最古老的數學書《算數書》的53題：

田一畝方幾何步？曰：方十五步三十一分步十五。術曰：方十五步不足十五步，方十六步有徐（餘）十六步。曰：并贏（盈）、不足以為法，不足子乘贏（盈）母，贏（盈）子乘不足母，并以為實，復之，如啟廣之術。

此題為求解方田一畝的邊長。其中一畝等於240步，240-225(15²)=15和256(16²)-240=16，解法為 。此為平方根近似值的另類解法，『等價於』逼近公式 。(例如， )。

        因此，Heath認為，幾乎不可能是偶然地有公式 ，這個式子給我們提供了想要的東西，從而得到阿基米德 的兩個近似值及其相互的關連。

參考文獻

Heath, T. L. (1912)， 《阿基米德全集（The Works of Archimedes）》，朱恩寬，李文銘等譯，陝西科學技術出版社。

Bunt, L. H. et al (1988), The Historical Roots of Elementary Mathematics. New York: Dover Publications, INC.

洪萬生(2000)，〈《算數書》初探〉，《師大學報：科學教育類》45(2): 77-91。