首次數B考題，沒有太大的問題。至少沒有數A有幾題選錯誤選項的比率異常高於選正確選項。我雖未參與此次數B考試閱卷工作，但與參與數B閱卷的人員閒聊之下，竟發現也出現和數A一樣的錯誤類型。其實我不太適合解說數B的題目，發現許多問題好像大家都會用應該或看起來怎樣就過去了，而我用比較嚴謹的看法反而將題目變難。不管怎樣仍本著盡量用最正確但簡單的方式講解，希望對中等程度學生有幫助。
對於素養題來看，個人覺得此題較契合我認知上的素養題。也就是整個問題的定義是用數學方式明確定義，而不是用文字描繪。可惜，當習慣用數學方式定義的人覺得一看就懂的事情，對於不熟悉這語言的人卻又看不懂了。此題答對率出奇的低，不過前$20\%$的考生與前$20\%\sim40\%$考生的鑒別度D1值相當的高，是所有考科的所有題目中最高的。這表示比起程度較好的考生，程度中上的學生大多不懂題意。關於本題的答對率與鑑別度，大考中心提供的分組資料如下（對各項目的說明，請參考111數A第一題的說明）：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 56 | 8 | 71 | 31 | 12 | 11 | 6 | 48 | 40 | 16 | 4 | 5 |
看了本題大考中心提供的選項分析資料，發現一個很有趣的現象，記錄下來分享給大家（對各項目的說明，請參考111數A第一題的說明）：
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | 16 | 22 | 14 | 21 | *27 |
| H | 0 | 9 | 10 | 6 | 18 | 57 |
| L | 0 | 21 | 29 | 22 | 21 | 8 |
當初做此題時（我覺得很難），很訝異這題會擺在多選的第一題。後來看到大考公佈答對率，這一題得分率為 $54\%$ 是多選中最高的。而成績前$20\%$的考生得分率為$82\%$（僅次於11題多點比較內積那一題），我原本預估高分組也不會這麼高的。以下是得分率與鑑別度(有關於多選題得分率的說明請參考111數A第9題的說明）：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 54 | 77 | 29 | 82 | 68 | 56 | 41 | 22 | 30 | 48 | 14 | 12 | 15 | 19 |
說實話，一開始沒弄懂此題，不知要怎麼做。原因是，我直覺以為打靶的靶子應該和射擊面是垂直的，所以一直思考靶子與平面所交的線段(長度為2)應該如何擺放。後來才猜想靶子是平躺的（一直搞不懂這樣怎麼打得到？）。這讓我想到前一陣子和一位研究做得相當好，在數學界頗有聲望的年輕數學家聊天。他告訴我，他看了今年數A的考題，覺得“十連抽”（13題）那題他完全讀不懂，看不出來要怎麼抽。近年來大家鼓吹素養生活情境題，看來我和那位在數學界有重要地位的年輕數學家，都屬於數學素養不夠的一群。
擺開情境的問題不說，這一題老師應該可以改一下給數A的學生做做看。不過選項(3),(4)要注意一下。這是近年來少見多選題選項不獨立的情況。害我在讀題的時候多看了好多遍，確認是否會錯意。所謂選項不獨立是指很明顯的兩個選項邏輯上是有關係的，例如這兩個選項就是互斥的（不可能同時對）。若將3個靶子依序標為 $A,B,C$ 然後選項分別改為：(3)可一次打中 $A,B$；(4) 可一次打中 $B,C$. 基本上是與原題問一樣的問題，卻可避免選項相關的問題。其實本題選項(3)(4)是最難的。一開始的想法是利用點到直線距離，將可打到每個靶子的斜率範圍一一求出比較。但這太複雜了，牽涉到二次不等式，最後還要比較根式的大小。看一下位置，知道要碰到$C$靶其斜率很小，且其切線斜率好求（選項(5)）。得到此切線再看 $(2,2)$ 和 $(4,6)$ 與它的距離大於$1$, 所以知道要打到這個靶子就打不到另外兩個，回答了原來選項的(3)是錯誤的。剩下可否一次打到$A,B$兩個靶子，看看圖形選項(2)的斜率拿來用，確實$(2,2)$與之的距離也小於$1$，因此解決了原來的選項(4)。
好難，從看懂題目到找到策略解決問題，大概花了15分鐘。實在很好奇同學，老師是怎麼處理這題的。網路上看了一下，大家幾乎都是畫圖得知，想想我真是白做工了。或許有人會認為畫圖得知也是數學素養的一部分，那真是再一次證明我的數學素養不足。好了言歸正傳，此題利用圖形判斷，再找到合適的方法驗證，是讓數A學生練習的好題目。不過選項應如前述修改一下（或改為計算題）。可考慮將選項(5)移前，以提示求切線。另外學生也可嘗試證明，若打到$C$就不可能打到$A,B$，以及若打到$B$一定也會同時打到$A$（較難）。
這一題，考生的答對率以及選項分析看起來還正常。要提它的原因是想提醒大家除了利用不等式處理問題外，也可用函數圖形的概念處理。我是不是很奇怪？前面打靶那一題，反對用圖形看出；而這題卻又希望大家能由圖形看出。其實兩者不同，前者關係到圖畫的精不精準，而後者與精不精準無關，完全在於解讀函數圖形。希望這函數圖形的觀點，能幫助學生更進一步了解函數圖形的意義，也希望對不等式的掌控較有困難的同學尋得另外處理問題的看法。選項(2),(3)是大家熟悉的平均數與標準差，這裡就不談。以下僅考慮與不等式有關的選項(1)(4)(5).
依題意，我們分別在坐標平面上畫出甲班的調整分數函數圖形 $y=0.8x+20$（以粗線表示）, 以及乙班的調整分數函數圖形 $y=0.75x+25$（以細線表示）. 注意兩直線交於點 $(100,100).$ 這圖形的意義很簡單，若要比較原始分數就看 $x$-坐標，若要比較調整過的分數就看 $y$-坐標。由於題目也要將原始分數和調整分數作比較（也就是比較 $x$-坐標與 $y$-坐標的大小），為了方便起見我們也畫出 $y=x$ 的圖形（以虛線表示）。如圖：
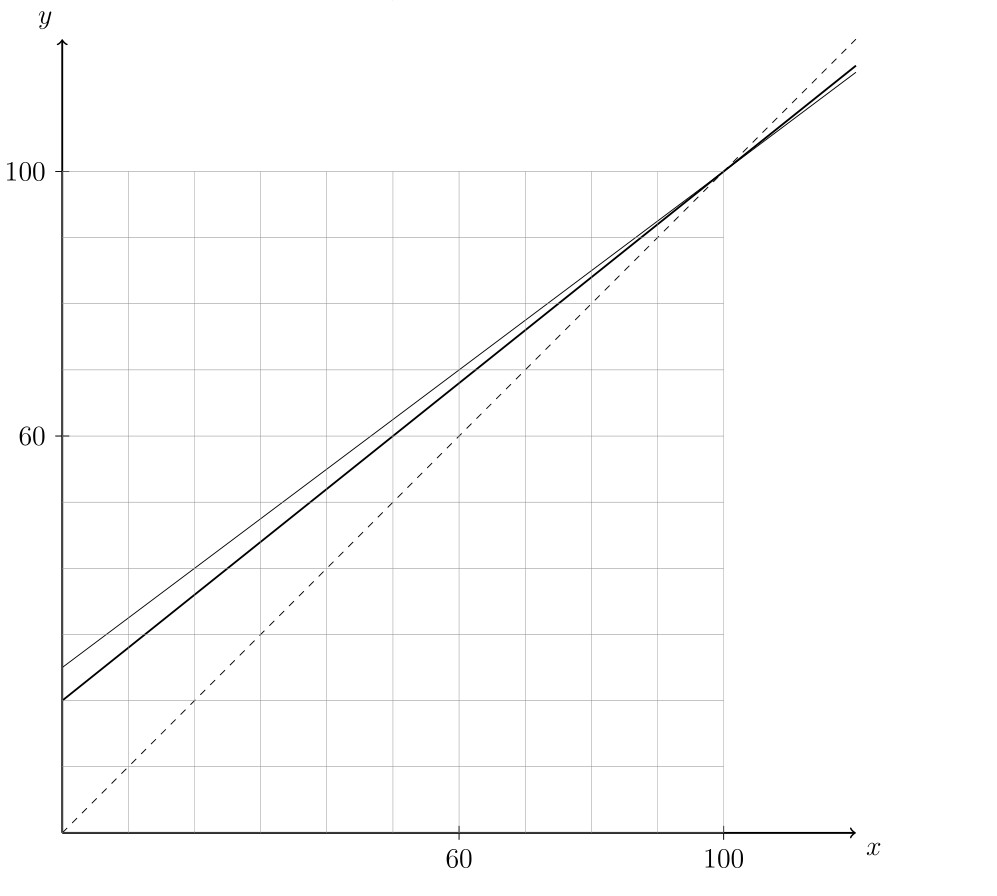
畫好圖形後，就可問學生能從圖形解讀什麼。例如乙班的圖形是遞增的（甲班也是），表示若以乙班兩個同學來做比較，分數較高者，在調整分數後依然會比較高。又在 $x\le100$ 時，固定 $x$ 發現乙班的 $y$ 值會大於甲班的 $y$ 值，表示原始分數相同的甲乙班同學，調整分數後，乙班的會高於甲班的。學生了解這些函數圖形的意義後，應該問他們能否回答選項(1)和選項(4)了。選項(1)當然由甲班的函數在虛線上方可得。而選項(4)不妨問學生是否由固定$y$值的水平線與甲班的函數圖形的相交情形以及與乙班的相交情形能知道什麼。學生應能辨識出調整分數後若甲班A同學與乙班A'同學成績相同，表示甲班A同學的原始成績較高，也因此可由遞增知乙班B同學調整成績後若低於A同學（表示也低於乙班的A'同學)，所以其原始成績會低於A'同學也因此低於A同學，故選項(4)是對的（其實者也可由固定$x$值來看，不過這樣的邏輯轉折比較多，學生可能較難弄懂）。選項(5)僅是邏輯問題，也就是說這個函數圖形只告訴我們原始分數與調整後分數的關係，根本無法讓我們知道有關人數的問題。由圖形知甲班原始分數不及格者還要加上原始分數介於50到60之間的同學，同理乙班的也要加上原始分數介於約47到60之間的同學。然而我們無從得知這兩班同學在這區間人數的多寡。
打靶那一題有這麼高的得分率，沒想到這題簡單的排列組合竟然全體考生僅有$7\%$的答對率，未免太低了吧(看來我對第8題仍耿耿於懷）！前$20\%$的考生也不到三成的學生答對。據大考中心資料，在數A跨考數B的考生中也僅有$9\%$的考生答對。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 18 | 0 | 27 | 4 | 1 | 0 | 0 | 18 | 23 | 3 | 1 | 0 |
不是很想談論排列組合的問題，不過看到這麼低的答對率（111數甲答對率最低的也是排列組合，第10題$14\%$），想說點東西，看看能否幫幫忙。其實我不是很贊成高一教排列組合，主要是學生數學成熟度還不夠，學一些較抽象的理論概念後，可以讓學生較能感受到怎樣的探討方式才能涵蓋全部情況，增加嚴密性的思維。老師應該也會覺得這部分很難教，教會了這個換一題就不會了。看到許多教學現場，老師教排列組合就是不斷的練習，詳細地告訴學生怎麼做。或許應該換個方式，教一些“錯誤”的方法，讓他們知道哪裡錯了。練習時，應該要求看到學生處理的方式，這樣才能知道他們錯誤的類型，增加可能的錯誤類型幫助他們。
閱卷工作這幾年來，幾乎沒看過高中生處理排列組合的問題，所以這裡僅能憑自己的感覺來想像學生可能犯的錯誤。學生往往都會有不同的想法，其他的可能情況，就靠老師與學生的互動了。學生常見的錯誤除了多算少算外，還有排列或組合搞不清楚。這一題要選學生站左邊或右邊（組合問題），然後要決定站那個位子（排列問題）。常看老師要學生記分辨排列或組合的口訣，真的沒必要，能以直覺方式了解它們的不同最好。另外還有可能的錯誤便是加法、乘法原理的誤用。
相信很多老師講解此題，直接就告訴學生用取捨原理。這裡我們用比較“笨”的方法進行。這樣狀況比較多，容易察覺學生可能出錯的地方。為了方便我們將站的位置編號，從左到右從1到6依序編號(1~3一邊；4~6另一邊)。同學也編號，女的是$A_1,A_2,A_3$, 男的是$B_1,B_2,B_3$, 其中 $A_3,B_3$ 不站一起。很自然的，學生會想的是怎樣將這些同學放在位子上。不過這有分你想先放那些沒有限制的同學$A_1,A_2,B_1,B_2$;還是有限制的$A_3,B_3$? 讓我們先做前者好了。先放$A_1$有6種選擇，接著放$A_2$。由於他們沒什麼限制所以$A_1$選好後，$A_2$有5種選擇，兩人合起來共$6\times5=30$種選擇。為什麼相乘呢？這很合理，今天甲若有$a$種選擇，而且甲選擇好後不管選哪一種，乙都有$b$種選擇，那當然總共有$a\times b$種選擇。但若甲選擇好了後，乙的選擇數會因甲選的不同而有所不同，那當然就不能相乘了。例如甲的選擇分成兩種情況，其中一種情況有$a_1$種選擇，且甲選此種情況之下乙都有$b_1$種選擇（因此在此情況兩人共有$a_1\times b_1$種選擇）；而另一種情況甲有$a_2$種選擇，且甲選此種情況之下乙都有$b_2$種選擇。這時兩人總共有$a_1\times b_1+a_2\times b_2$種選擇。所以目前計算$A_1,A_2$兩人合起來共$30$種選擇沒問題。好，我們繼續下去，讓$B_1$來選。$A_1.A_2$選定後，$B_1$怎麼選都不會和題目的要求抵觸，所以他都有$4$種選擇，因此$A_1,A_2,B_1$三人總共有$30\times4=120$選擇。接下來換$B_2$了，依然隨意放都不會抵觸，不過要注意，有些情況當$B_2$選擇後，會造成$A_3,B_3$剩下的選擇，都會與題設抵觸。或許學生認為沒關係，先選了以後再扣掉那些會抵觸的，很好!這樣他們就懂得用取捨原理了。也可考慮$B_2$就停下來不選，先將前面$A_1,A_2,B_1$的選擇分類。例如分成 $A_1,A_2,B_1$ 都在同一邊；$B_1$和$A_1,A_2$其中一個在同一邊，另一個在另一邊；$B_1$在一邊，$A_1,A_2$在另一邊。 這時候每一類有多少種，學生可能會算錯，最後加總驗算一下，若是前面算的$120$，那大概錯不了。分好類後最後僅剩三位，就好算了。例如$A_1,A_2,B_1$都在同一邊的情形，由於$A_3,B_3$一定在同一邊，所以他們僅能站在 $1,3$ 或 $4,6$。不過其他情形就又要分$A_3,B_3$是否在同一邊來討論，因為這兩種的個數又不一樣囉。總之，先放沒有限制的並沒有想像中的簡單，原因是他們雖沒限制，但最後需用分類的方式才能將有限制的放好。不過此時若發現會抵觸的情況較少，馬上考慮取捨原理會快很多。
我們看看先放有限制的$A_3,B_3$會怎樣。因為有限制，不能隨便亂放，所以就可先分類好，再隨便放沒限制的就可以了。我們可分成$A_3,B_3$在同一邊和不同邊兩類。同邊時，按題意$A_3,B_3$只能在 $1,3$ 或 $4,6$。排好後，其他人就可隨意排（也就是每種情形有 $4!$ 種排法）。不同邊時，其他人幾乎仍可隨意排，不過要排除男女分別都在同邊的問題，此時僅剩這種情況要排除，應該可理解搭配取捨原理馬上就可算完。同樣的，若不喜取捨原理，$A_3,B_3$不同邊時，我們可以想像讓六人分成兩組，一組有$A_3$, 另一組有$B_3$. 由於不能 $A_1,A_2,A_3$ 同一組，所以共有$5$種分組。記得分好組後同組的就可以隨意排，此時每種分組會有 $3!\times3!$ 種排法（而不是 $6!$, 否則分組幹嘛？）。這個做法結合組合與排列，應該鼓勵學生這樣做做看（原因不是它好不好算，而是從計算中讓學生理解組合與排列的差異）。學生應該從這裡可以看出若要直接算(即不用取捨原理），先從有限制的著手分類，會比從沒限制的著手分類好算多了。本題答對率這麼低，估計很多考生都由沒限制的直接算，或許這樣的解釋會讓他們印象深刻。
從前面探討我們可以看出，處理有限制的排列組合問題，可以考慮取捨原理將不合限制的情況排除。 本題要排除的狀況不複雜。不過有時要排除的狀況稍複雜，不想用取捨原理，可考慮先從有限制的物件擺放分類處理。分類時最容易出錯，注意要涵蓋所有狀況，也不要有重複的情況發生。計算每一類的個數時，適時搭配取捨原理以及對稱性（本題的對稱性學生應很容易理解）可以簡化一些計算。
