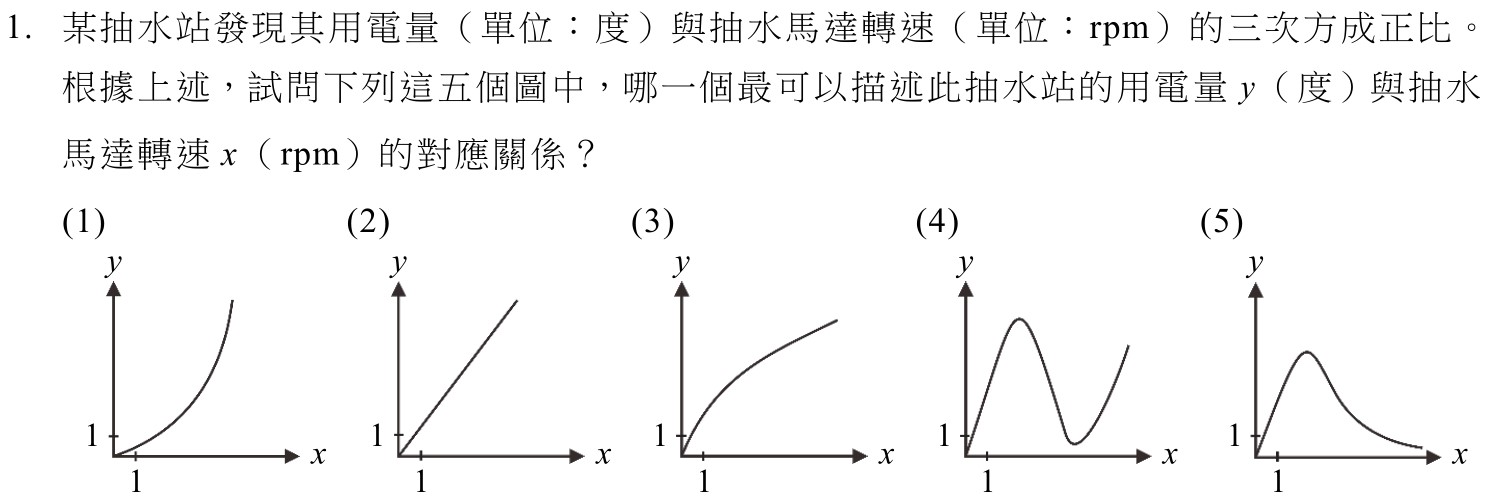
此次數B考題，一般普遍認為比去年數B難，成績公佈後，確實頂、前、均三標都比去年少了一級分，有趣的是後標和底標卻也各比今年數A的後標和底標少了一級分。數B考科是一個尷尬的角色，原先數B是設定讓數學需求度低的學生學習，但卻又有許多校系將數B列入個人申請比序參採科目。要達到評鑑的功效，題目自然就不能太簡單。老實說對於數學需求度低的學生這份卷子算是難，不過參加數B的考生絕不是只有數學需求度低的學生，所以這樣的考題就還OK了。就舉今年來說，幾個當初課綱在數B弱化了學習目標而導入讓學習數B學生“欣賞”數學的題材，都拿來考了且難度不低。這確實達到讓數A跨考數B的學生分數不要衝太高的目的，但這樣的難度也不會讓原本選讀數B的學生佔到什麼便宜。大家都心知肚明，學生數學程度的差異性大，對於數A跨考的考生，數學成績的差距足以彌補其他科目之不足。依現在的氛圍，數B考科已經儼然變成數A成績不佳的原本修習數A學生的庇護所。對於學習數B的學生在刻意安排降低學習內容以及數學訓練的成熟度後，還要和一些數學訓練及成熟度高的人一起競爭他們能力所不能及的競賽，真的對他們不公平。建議大考中心以及大學相關科系，能將數學B這個考科僅視為能力檢定的考科。它的五標僅作為學生申請的一個門檻依據，而不將其級分加入成績的比序。這樣大家也就不在乎有多少人滿級分了。讓課綱當初訂定數學B學習內容的“美意”，對於這群所謂數學需求度低的學生有實質上的幫助，而不是讓他們在考場上受到二次傷害。
單選題：此次單選部分，按照大考中心的難易度分類，易的題目（答對率$60\%$以上）有3題（第2,4,5題）；中易的題目（答對率$60\sim45\%$）有3題（第1,3,6題）；中難的題目（答對率$45\sim30\%$）有1題（第7題）。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 46 | 71 | 20 | 77 | 60 | 48 | 31 | 14 | 51 | 17 | 12 | 17 | 17 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | *46 | 13 | 16 | 24 | 2 |
| H | 0 | 71 | 2 | 6 | 21 | 0 |
| L | 0 | 20 | 28 | 26 | 23 | 4 |
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 39 | 23 | 43 | 31 | 29 | 29 | 20 | 16 | 12 | 2 | 0 | 9 |
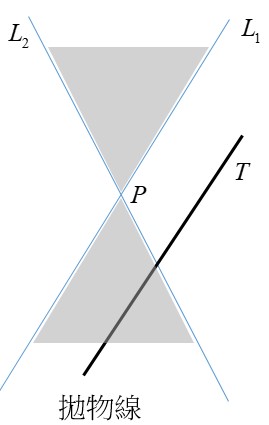
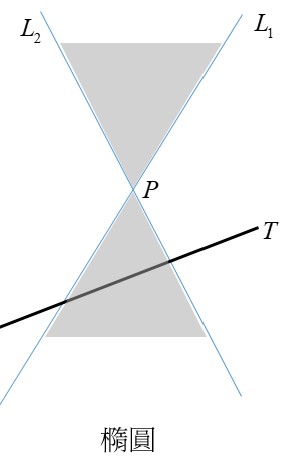
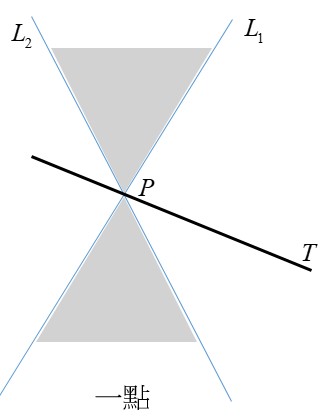
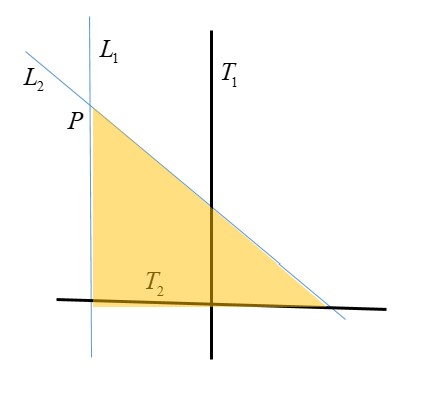也就是先畫出代表牆面的鉛直線 $T_1$，依題意墻面上的截痕是拋物線，所以依前面所述我們畫出與 $T_1$ 平行的 $L_1$，再畫 $L_2$ 與 $L_1$ 夾銳角($60^\circ$)。由於地面與牆面垂直，我們可畫出代表地面的水平線 $T_2$ （與 $T_1$ 垂直）。儘量延伸 $T_2$，我們會發現它與 $L_1,L_2$交於 $P$ 點的同側 （這是因為夾角為銳角），所以在地面的截痕為橢圓，又$L_1,L_2,T_2$所圍的三角形不是以$T_2$為底的等腰三角形，所以此截痕不會是圓（即兩軸不等長）。為什麼前面說要儘量延伸 $L_1,L_2$ 呢？例如本題若將夾角改為鈍角（廣角的手電筒）那麼將$L_2$ 延伸出去如圖
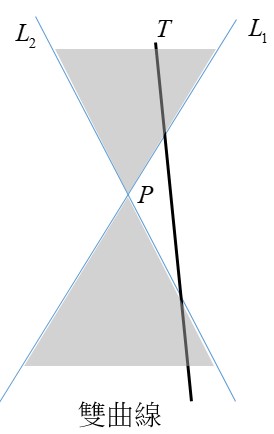
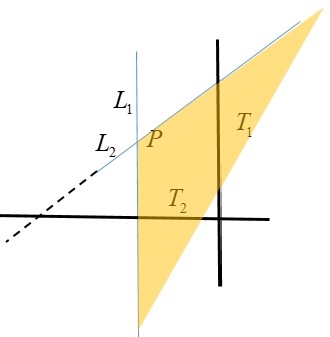學生才能知道其實 $T_2$ 與 $L_1,L_2$ 都相交，只是交在 $P$ 點的異側，所以截痕會是雙曲線的一支。
其實圓錐截痕還有以下退化的情形：
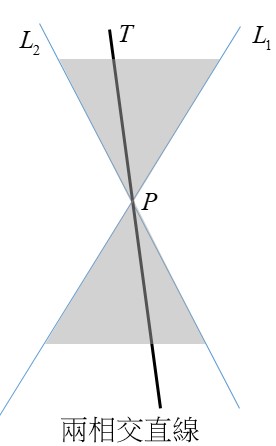
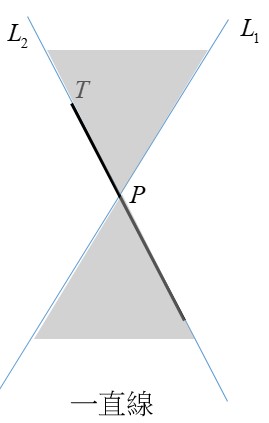
一開始我只注意到“數學”上的條件（即“半滿”）而誤以為水面會將杯子的上下底各分割一半，因此錯將水面所代表的直線 $T$ 畫通過 $P$ 而錯答為兩相交直線。其實此題談的是“物理”的性質（即水面保持“水平”）。我們可以先畫代表置於水平桌面杯子側面邊緣的水平直線 $L_1$，再畫另一邊的側面邊緣 $L_2$ （記得儘量延伸），再將代表水面的水平直線 $T$ 如圖畫上：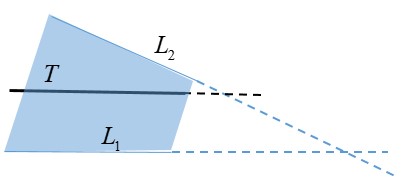
就可以看出截痕為拋物線了。
多選題：此次多選部分，按照大考中心的難易度分類，易的題目（得分率$60\%$以上）有1題（第8題）；中易的題目（得分率$60\sim45\%$）有1題（第10題）；中難的題目（得分率$45\sim30\%$）有1題（第9題）；還有兩個（得分率低於$30\%$）難的題目（第11,12題）。
| # | P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 29 | 45 | 16 | 52 | 33 | 26 | 19 | 14 | 8 | 29 | 19 | 7 | 7 | 5 |
| 12 | 28 | 49 | 15 | 60 | 30 | 19 | 15 | 15 | 12 | 34 | 30 | 11 | 4 | 0 |
為什麼拿11,12題的得分率一起做比較呢？不是因為兩題皆為難題，而是第11題的整體得分率，比第12題的整體得分率高了$1\%$，但高分群不管是成績在前三分之一的得分率Ph或前$20\%$的得分率Pa，第11題都比第12題低。就連全對率T也是如此。第12題得分率低是可以預期的，
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | *61 | 31 | 49 | *63 | 54 |
| H | 0 | 73 | 11 | 34 | 75 | 53 |
| L | 0 | 43 | 52 | 58 | 50 | 50 |
本題成績表現在後面三分之一的低分組（L）的選項分析，不具參考價值（每個選項幾乎都有一半的考生選，看來大多是猜答）。至於表現在前三分之一的高分組(H)考生，一般容易的選項幾乎都會有八成（甚至九成）以上的高分組考生答對（即對的選項圈選的比率會高於 $80\%$，而錯誤的選項圈選的比率會低於$20\%$）。從這個角度來看對於大部分高分組考生，只有選項(2)是容易的。這頗令人訝異，因為選項(3)問的是$P$點是否在圓內？由題意知道此圓的半徑為$a$，應該沒問題；而$P$到圓心的距離為 $a+c>a$ ，自然$P$在圓外這樣基本的觀念竟然有三分之一以上的高分組考生不知道，是不是很令人疑惑?或許大家太關注於圓的方程式，而忽略了強調圓的幾何意義，以致於不會判斷一個點是否在園內。課綱要求不去利用圓心與半徑關係探討兩圓的關係，造成學生對於圓的基本幾何概念薄弱或許是一個因素。另外，我對選項(1)有點意見。照理說符合條件的$A$點有兩個選擇，即 $b=a$ 或 $b=-a$。問題是要排除 $b=-a$ 會造成與題設 $a>c$ 矛盾，並不是馬上可以看出來的（反而選項(2)(3)較直接）。然而若學生一開始就認為 $A$ 點在第一象限，根本不會花時間檢查這一點，反而小心一點的考生要花時間排除 $b=-a$ 的情形。既然這樣的選項，無法評量考生是否知道 $A$ 點原本有兩個可能，題設便應該一開始就假設 $A$ 點在第一象限（這樣選項(1)依然是個合理的問題）。知道 $A,P$ 點坐標分別為 $(a,a),(c,c)$，便有很多方法處理選項(4),(5)。例如利用 $\overset{\displaystyle{\rightharpoonup}}{AP}=(a-c,a-c)$ 且其長度為 $a+c$，或是用 $\overline{OA}$ 等於 $\sqrt{2}a$ 也等於 $\sqrt{2}c+a+c$ 處理。在數A高分群的考生中對於處理這些抽象符號的運算大多沒什麼問題，選項(4)(5)高分群表現不佳，是不是修習數學B的學生（即使是高分群的學生）在抽象符號的運算這方面仍有待加強？另外依據過去閱卷以及教學現場觀察的結果，我發現學生解題，通常是看到題目所假設的條件，也不管題目問什麼，就先將這些條件能推演的結果一個一個列出來，再回來回答問題。這樣的習慣很不好，尤其在處理多選的問題時，往往有些選項是有提示性的；先不管選項問什麼不只花費了許多不必要的時間還有可能做白工。個人估計，此題會不會有許多考生以為 $a,c$ 有固定解，所以花了很多時間想將之解出。然而由於解不出，因此就不知如何代入選項了。其實選項中已明白告知 $a,c$ 有一定的比例關係。所以希望老師多多注意學生是否有這樣的問題，要學生多注意題目各選項間的連貫性，有了問題整體概念再作答，不要盲目作答。
選填題：此次選填部分，按照大考中心的難易度分類，第13題是介於中偏易和中偏難之間的題目（答對率$45\%$）；第14,15題為中偏難；而第16,17題得分率低於 $30\%$ （甚至低於 $20\%$）是難題。第16題摺紙問題，大家可能受國中處理過類似問題所影響，想用幾何方法處理。其實若知道架坐標處理，應該不難。第17題是排列組合問題，近年來大考的排列組合問題都不難，可是考生表現都不佳。這裡就拿選填的兩題排列組合問題（第14,17題）來討論。
| # | P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 38 | 72 | 7 | 82 | 53 | 34 | 17 | 3 | 65 | 29 | 19 | 17 | 14 |
| 15 | 38 | 78 | 6 | 87 | 59 | 30 | 11 | 4 | 72 | 28 | 29 | 19 | 7 |
第14,15題皆為中偏難，高分組的表現尚可（對他們屬易），但低分組的表現與之落差很大（少了猜答機會，這是選填題普遍情況）。第14題是操作型的問題，而第15題較需觀念作答。
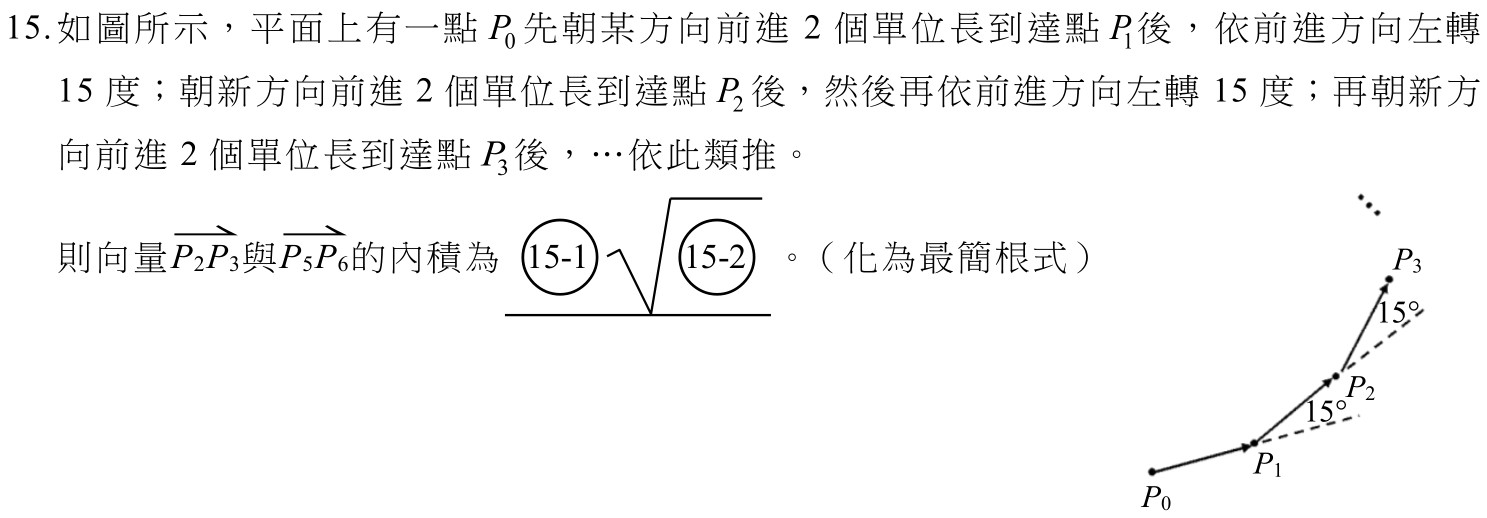
排列組合的問題，不必強調太技巧性的算法（例如，看出 $a,c$ 必需同奇同偶，所以是$10$個奇數中選兩個加上$10$個偶數中選兩個）；但也不要只叫學生排排看就好。可以告訴學生儘量用分類的方法計數。所謂分類就是要每個元素都要被分到一類，而且不同類不會有共同的元素。如此就能確保算出的個數不多也不少。當然了，分類的方法可能有很多，另一個要點就是，每一類的個數都好算。就拿14題來說，我們可以先想想如何將這些等差數列分類。這就關係到如何決定一個等差數列。學生應該都知道，只要知道公差以及某一項就可決定一個等差數列。所以我們可以用公差來分類，然後再利用其第一項（或第二項、第三項）來計算每一類有多少個符合題設的等差數列。例如公差是$1$, 的就有第一項是 $1,2,\dots,18$ 這 $18$ 個數列；公差是$2$, 的就有第一項是 $1,2,\dots,16$ 這 $16$ 個數列；公差是 $3$ 就有 $14$ 個；...。由這些例子應該可以猜出規律，就是公差是 $d$，就有 $20-2d$ 個數列。所以最後一類應該是公差是 $9$ 的有$2$ 個。檢查一下沒有錯就可已確定共有 $18+16+\cdots+4+2=9(18+2)/2=90$ 個。
當然了，我們也可以用第一項（或第二項、或第三項）來分類。由於這是三項的等差數列，用等差中項（即第二項）來分類（每一類再用公差來計算其個數）應是不錯的選擇。第二項為 $2$ 的只有公差為 $1$ 的 $1$ 個數列；第二項為 $3$ 的有公差為 $1,2$ 的 $2$ 個數列；第二項為 $4$ 的有 $3$ 個數列；...。由這個規律看起來好像第二項為 $b$ 的有 $b-1$ 個數列，不過要注意例如在第二項為 $19$ 的情況只能有公差為 $1$ 的這一種，所以很顯然的，中間有轉折，公差不能越來越大下去。再仔細檢查，第二項為 $10$ 的有公差為 $1,2,\dots,9$ 的 $9$ 個數列（公差10的話，第一項會是$0$）；但是第二項為 $11$ 的情況就變成仍然有公差為 $1,2,\dots,9$ 的 $9$ 個數列（公差10的話，第三項會是$21$）。接下學生應可理解第二項超過$11$後，隨著第二項變大，有同樣第二項的數列個數就變少，也就是第二項為 $12$ 的有 $8$ 個：第二項為 $13$ 的有 $7$ 個；每類個數一直遞減到第二項為 $19$ 的有 $1$ 個。因此總共有 $1+2+\cdots+9+9+8+\cdots+1=90$ 個。也可讓學生試試看以第一項來分類，能否歸納出計算每一類個數的方法。這樣用第一項的分類法，或許有的學生會覺得歸納出每類的個數困難度較高。我們不是每種分類法都要會算，重要的是讓學生知道，有時分類的方法會影響計算的難易度。用某一分類法計算時，若覺得複雜，換一個分類的方式或許會有幫助。接下來讓我們用分類的方法算一算最難的第17題。
第17題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 25 | 3 | 35 | 8 | 4 | 3 | 2 | 22 | 27 | 4 | 1 | 1 |
有老師提及一個很快速的看法，本題的例子已給很大的提示：考慮 $n=3$ 的情形，可將要計算的序列分成 $00X$ 和 $X00$ 兩種類型，其中 $X$ 可以是 $0,1,2$ 中任何數。所以 $00X$ 和 $X00$ 各有三種。過去在計算個數時由於 $00X$ 中的 $000$ 與 $X00$ 中的 $000$ 重複計算因此只有 $3+3-1=5$ 種，然而本題（反其道而行）反而 $000$ 要算兩次不扣除，所以有 $6$ 次。同樣的 $n=5$ 時可考慮 $00XYZ$, $X00YZ$, $XY00Z$, $XYZ00$ 四種情形，每種情形有 $3^3=27$ 個，又不扣掉重複的部分，故共有 $4\times 27=108$ 個。這個方法真是又快速又準確。不過我們不是只要教學生會做這一題就了事，試想在考試這麼簡短的時間，能精準掌握這樣的方法且確認無誤而敢使用的人幾乎微乎其微。還是教學生正常分類的方式計數為要。
讓我們用最簡單直覺的方式分類，也就是以5位數中 $0$ 的個數來分類，然後再在每一類中依 $0$ 出現的樣式來計算 $00$ 出現的次數。從最簡單的 $5$ 個 $0$ 開始。這一類當然只有一個五位數 $00000$，所以依題意 $00$ 出現 $4$ 次。接著就是 $4$ 個 $0$ 這一類，因為有 $5$ 位數要放 $4$ 個 $0$，所以這一類又可分成以下 $C_4^5=5$ 個子類：$0000X,X0000$, $000X0,0X000$ 以及 $00X00$。因為 $X$ 僅能是 $1$ 或 $2$，每一種皆有 $2$ 個五位數，但前兩個 $0000X,X0000$ 其 $00$ 出現 $3$ 次；後三個 $000X0,0X000$ 以及 $00X00$ 其 $00$ 出現 $2$ 次。故總共 $00$ 出現 $2\times (2\times 3+3\times 2)=24$ 次。接著是有 $3$ 個 $0$ 這一類：由於 $5$ 個位數要有 $3$ 個 $0$，照理說會有 $C_3^5=10$ 個子類，不過我們排除沒有出現 $00$ 的情況（即 $3$ 個 $0$ 皆分開的 $0X0Y0$ 這一子類），可分成三個 $0$ 在一起的 $000XY,X000Y,XY000$ 這 $3$ 個子類，以及剩餘有兩個 $0$ 在一起且與另一個 $0$ 分開的 $10-1-3=6$ 個子類（即 $00XY0,00X0Y,0X00Y,X00Y0,0XY00,X0Y00$）。注意，我們僅需知道每種 $0$ 連續出現的類型的個數，不必浪費時間真正列出這些子類（除非擔心算錯）。因每一個子類有 $2^2=4$ 個，又三個 $0$ 在一起的那 $3$ 個子類 $00$ 出現 $2$ 次；而兩個 $0$ 在一起且與另一個 $0$ 分開的 $6$ 個子類 $00$ 出現 $1$ 次，故這一類 $00$ 出現 $4\times(3\times 2+6\times 1)=48$ 次。最後僅剩有 $2$ 個 $0$ 這一類：我們僅要算兩個 $0$ 在一起有 $4$ 個子類（即$00XYZ$, $X00YZ$, $XY00Z$, $XYZ00$，仍不必列出，這裡列出只是為了解釋）。每個子類有 $2^3=8$ 個，故這類中 $00$ 出現的次數為 $8\times(4\times 1)=32$ 次。全部算完後加總，共有 $4+24+48+32=108$ 次。
當然了，我們也可直接用 $00$ 出現的次數分類，即分成 $00$ 出現4次（五個$0$）；$00$ 出現3次 （四個$0$皆在一起）；$00$ 出現2次（三個$0$在一起或兩個$0$在一起兩次）；以及 $00$ 出現1次這 $4$ 類。再在每一類中依 $0$ 的個數計算 $00$ 的次數。例如 $00$ 出現1次的，又可分成有三個$0$和兩個$0$，這兩種。三個$0$的有 $00XY0,00X0Y,X00Y0,0X00Y,0XY00,X0Y00$ 這 $6$ 個子類；兩個$0$的有 $00XYZ$, $X00YZ$, $XY00Z$, $XYZ00$ 這 $4$ 個子類。所以 $00$ 出現1次的共有 $2^2\times 6+2^3\times 4=56$ 個。其餘類別用類似方法，我們有 $00$ 出現4次的有 $1$ 個；$00$ 出現3次的有 $4$ 個：$00$ 出現2次的有 $18$ 個。所以總共 $00$ 出現的次數為 $4\times 1+3\times 4+2\times 18+1\times 56=108$
關於第20題，若了解題意照著做當然不難。不過前面所述，在電線桿上的點之間的比例和畫在畫布上的比例是一致的，但為何三根電線桿底座間距相等，畫在畫布上間距卻會不同呢？為何沒有保持等比例呢？學生或許會有這樣的疑惑與困擾。最後，就讓我們大致探討一下這個問題。單點透視法一個要注意的概念就是一般來說它不會保持原來長度間的比例關係。否則“消失點”（可以把它想像為類似無窮遠點的概念）就沒辦法畫在有限的畫布上。從這個概念來看，原來一樣間距的點，畫在畫布上若越靠近消失點就會顯得越短。所以三個電線桿底座雖間距相等，但它們所對應的點$A_1,A_2,A_3$，由於 $A_1,A_2$ 比較靠近消失點，所以 $\overline{A_1A_2}$ 應該會短於 $\overline{A_2A_3}$。另一個有關於單點透視法要注意的概念就是，平行線未必仍保持平行。像題目中電線桿底座的連線以及頂端的連線是平行的（因為電線桿高度相等），不過畫在畫布上它們相對應的直線 $L,M$ 卻不平行。然而題目中三個互相平行的電線桿，依題意畫在畫布上依然平行（皆與$y$軸平行）。就是因為它們依然平行，讓它們保有特殊的性質。還有一個關於單點透視法要注意的概念就是原來不同的點可能畫在畫布上同一點，要把三維空間的物體畫在二維平面上，這個還蠻好理解的，不過與本題沒有太大關係，就不多談了。剛才談的是空間的世界利用單點透視法畫在平面上無法保持的性質；至於單點透視法仍保有的性質就是：若原來空間中兩點 $P,Q$ 畫在畫布上為相異點 $P',Q'$，則直線 $PQ$ 上的點畫在畫布上依然會在直線$P'Q'$上。這也是本題所用到的概念。假設我們是垂直面對三個電線桿所在平面，在畫布上畫下第一、第三根電線桿後，如何畫上第二根電線桿呢？由於電線桿的頂點、底部的連線段以及第一、第三根電線桿圍成了一個矩形，其對角線的交點就是第二根電線桿的中點。所以我們只要在此交點上畫一個與第一、第三根電線桿平行的線即可畫出第二根電線桿的位置。如圖示：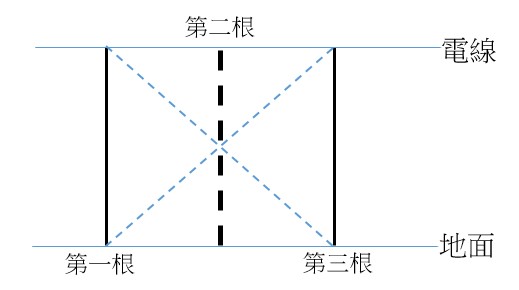
同樣道理，如本題，當視角沒有正對三個電線桿所在平面（且離第三根比較近）時，我們依然可用前面所述的方法由第一、第三根電線決定第二根電線桿在畫布所在的位置。原來的兩個對角線對應到畫布上的線段$A_1B_3$與線段$A_3B_1$，也因此第二根電線桿的中點（即兩對角線交點）就會對應到畫布上直線$A_1B_3$與直線$A_3B_1$的交點（令之為 $R$），也因此依題意通過$R$畫與直線$A_1B_1$（及直線$A_3B_3$）平行的直線就是$A_2,B_2$所在的直線。
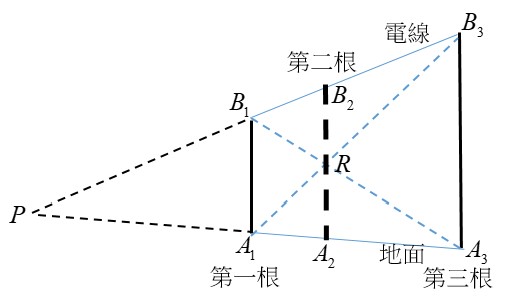由於直線$A_1B_1$與直線$A_3B_3$平行且$\overline{A_1B_1}:\overline{A_3B_3}=1:2$ 利用相似形，我們知道 $A_2$ 會在線段 $A_1A_3$ 上距離 $A_1$ 三分之一處（即 $\overline{A_1A_2}:\overline{A_2A_3}=1:2$），而不是中點。這也符合前面所述 $\overline{A_1A_2}$ 應短於 $\overline{A_2A_3}$。
不過同樣利用直線$A_1B_1$與直線$A_3B_3$平行以及相似形，可得$R$依然會是$A_2,B_2$的中點。也就是說原來第二根電線桿的中點，畫在圖上依然是中點。事實上$A_1,B_1$的中點和$A_3,B_3$的中點連線會通過消失點$P$以及$A_2,B_2$的中點$R$。這也和原來三根電線桿的真實情況相吻合。因為三根電線桿等高，底座又在同一直線上，所以底座的直線與頂端所在直線是平行的，且與三根電線桿的中點連線平行。所以這三條平行線在單點透視法中所畫的直線會交於消失點$P$。現在大家應可大致了解，原來平行的三根電線桿利用單點透視法畫在畫布上由於依然平行，所以利用相似形概念可知，同一電線桿上的點畫在畫布上，其位置的比例關係是不變的。
結語：從這次數學B的考題，以及學生表現，忍不住想下個結語說說自己的看法。數學B宣稱是讓未來數學需求度低的學生修習，其實直白的說，這些學生大多都是數學能力較差的學生。課綱要凸顯數學B與數學A的不同，所增加的題材雖可說是希望學生以“欣賞”的角度讓學生了解一些以後可能會接觸的數學相關概念；但這些數學概念對數學成熟度不夠的學生仍是困難的。所以這些題材“欣賞”可以，拿來考試，大多數學生可能就“無福消受”了。就舉單點透視法來說，學生空間概念已不足，又要學空間到平面的轉換豈不更困難（當初不學投影不就是因為這原因嗎？）。雖然此次題目，不需真正了解太多概念，只要照著做就好；但是太多的點和線，一下在原來的空間、一下在圖上，沒有完整的概念當然容易搞混。所以在閱卷場上，看到考生代錯點、弄錯直線的比比皆是。近幾次的課綱演變，都有著一個怪異現象，就是會有一些新的題材加入，而下一個課綱會捨去或弱化這些新的題材（例如信賴區間、插值多項式等），但卻又加入另一些新的題材。然而在內容與教學現場沒有充分溝通之下這些新的題材都把大家搞得烏煙瘴氣的。造成不同代的學生都還要花一些時間去學一些前一代和後一代都沒學卻又很難搞懂的東西。弄得老師也苦、學生也苦。個人建議回歸基本內容，尤其是數學B更不需學多學雜。只要基本概念正確、邏輯推演能力夠成熟，將來遇到所需的數學時，自然能弄懂。數學不正是因為這樣才能在各方面有所應用嗎？而不是為了某個應用，而刻意的片面學習該處的數學。