
此次分科數甲考題,除了幾題計算稍顯複雜外,基本上沒有太難的題目。不過仍有幾題答對率低於預期,尤其是幾題不難的問題可能牽涉到符號操作,而不是具體的數字計算,作答的情況非常不理想。例如單選的2,3題以及多選的4,6題,都是沒有具體的數字可以計算,對大部分學生來說應該是困難的。造成不必計算的部份無法得分,而需計算的部分又有點複雜也得不到好處,這可能就是成績不如預期的原因。
單選題一般來說應是穩定軍心用的,不過沒想到2,3兩題考生的表現並不是如此,應該是學生對符號操作的能力欠佳有關。關於單選的三題,考生作答的 PD 值如下:(關於 PD 值請參考大考中心“一起來認識學測與指考的試題答對率”)



讓我們回到今年的第3題。題目選項已表明要考慮積分的區間是 $[0,3]$。高中教的黎曼和僅考慮將區間均分的情況,所以一般來講每個分割的間距$\triangle x$應是每單位長分成$n$等分,即$\triangle x=\frac{1}{n}$(如上面110那題);或是整個區間$[0,3]$分成$n$等分,即$\triangle x=\frac{3}{n}$。知道可能的$\triangle x$後接下來便是要知道每個分割區間的端點,以便將區間上的點代入被積分的函數。若 $\triangle x=\frac{1}{n}$,則在區間[0,3]所分割出的$3n$等分中各區間的端點依序為$0,\frac{1}{n},\frac{2}{n},\dots,\frac{3n-1}{n},\frac{3n}{n}$;而若 $\triangle x=\frac{3}{n}$,則在區間[0,3]所分割出的$n$等分中各區間的端點依序為$0,\frac{3}{n},\frac{6}{n},\dots,\frac{3n-3}{n},\frac{3n}{n}$。也就是說,若$\triangle x=\frac{1}{n}$,則黎曼和應該要有$3n$項;而若$\triangle x=\frac{3}{n}$,則黎曼和應該要有$n$項。看看題目,發現僅有$n-1$項(這有點奇怪),不過和$n$項僅差$1$項(事實上只要差固定的有限項)最後算極限時差距會趨於$0$所以極限會一樣,因此本題應是以$\triangle x=\frac{3}{n}$來分割的黎曼和。了解這點就不難發現選項(3)才是正確的。
其實學生到高三已學會$\Sigma$這個summation符號,應該讓學生用$\Sigma$來表示黎曼和,較容易看出此極限是哪一個定積分(或許這也是考題故意不用$\Sigma$來表示的原因)。原式可表為 $\displaystyle\sum_{k=1}^{n-1}\frac{3}{n^2}\sqrt{4n^2+9k^2}$。因為有$n-1$項所以知道$\triangle x=\frac{3}{n}$,每個分割區間的端點為$\frac{3k}{n}$,故原式可寫成$\displaystyle\sum_{k=1}^{n-1}\frac{3}{n}\sqrt{4+\left(\frac{3k}{n}\right)^2}$。而此和與$\displaystyle\sum_{k=1}^{n}\frac{3}{n}\sqrt{4+\left(\frac{3k}{n}\right)^2}$僅差一項$\frac{3}{n}\sqrt{4+3^2}$,因此當$n$趨近於$\infty$時會趨近於同一極限$\displaystyle\int_0^3\sqrt{4+x^2}\,dx$。
這題的轉折$n-1$項(而不是$n$項)以及每個分割的長度$\triangle x=\frac{3}{n}$(而不是$\triangle x=\frac{1}{n}$),可能就是造成得分率低的原因。我們從以下考生的選項分析可見端倪。
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | 3 | 9 | *21 | 47 | 19 |
| H | 1 | 1 | 3 | 32 | 54 | 9 |
| L | 1 | 5 | 16 | 12 | 41 | 26 |
多選題中考生的表現,依大考中心的分類,除了第5題為中偏易外,其餘為中偏難到難。這裡就大致談一下較難的那幾題。考生成績的 PD 值如下:
會特別談這一題是看到很多老師在解說此題時,直接就考慮$a=2$, $b=5$ 的情況。或許老師這樣處理的用意,是考量前面提的學生對符號操作不熟悉,所以用具體數字教學生處理。但這是不正確且非常危險的。首先學生可能誤以為由題設,$a,b$就一定是$2$和$5$,再加上若真的用$a=2,b=5$作答此題,每個選項都能答對,更會誤導學生以為這是正確的解法。事實上題目是要考慮所有符合題設的$a,b$,當然不能用特定的$a,b$來決定其他的情況是否會對。或許有老師認為「$a=2,b=5$是符合題設的最小區間,若對於最小區間是對的,那對更大的區間當然也就對了。所以這樣的解法沒有問題」。這乍聽之下好像滿合理的,不過事實上仍不正確。選項(3)就很可能出問題。例如題目改為$-2,2$滿足$|x-a|\le b$。此時滿足的最小區間為$a=0,b=2$,而且$-1,1$仍滿足$|x-a|\le\frac{b}{2}$。但當$a'=2,b'=4$時,$-2,2$滿足$|x-a'|\le b'$,可是$-1,1$就不滿足$|x-a'|\le\frac{b'}{2}$了。所以對最小的區間成立,並不代表對一般的區間仍成立。更何況若原來題目是考慮$|x-a| < b$,那就找不到$a,b$會是會是所謂的最小區間了,那怎麼辦?所以還是要回歸用抽象的符號讓學生操作。
整個操作並不難,大家應該都了解 $|x-a|\le b$ 等同於$ a-b\le x\le a+b$。接下來就是單純的不等式問題了。也可鼓勵學生用區間的概念來看這個不等式。有了區間概念就知道本題主要的關鍵就是 $-3,7$,額外 $-1,4$ 的條件是多餘的,反而會造成干擾。看到有些老師解題時還把$-1,4$拿來驗證,就失去了讓學生了解區間概念的機會了。至此我們知道本題的條件就只有 $7\le a+b$ 以及 $a-b\le -3$ 而已。由此不等式,可以解得 $b\ge 10$,而若 $b=a$ 馬上得 $0\le -3$ 的矛盾,選項(1)、(4)、(5)應該算簡單。選項(2)只是問是否 $-7\ge-a-b$ 以及 $3\le-a+b$。因為和原不等式一致所以正確。而選項(3)問的是可否推得 $\frac{7}{2}\le a+\frac{b}{2}$ 以及 $a-\frac{b}{2}\le -\frac{3}{2}$,這當然就不對了。其實選項(5)有很好的提示作用,可以幫我們找到選項(3)錯誤的反例。選項(5)告訴我們當 $b=a$ 時 $|x-a|\le b$ 不可能有小於 $0$ 的數在之中,所以選項(3) $|x-a|\le \frac{b}{2}$ 在 $a=\frac{b}{2}$ 的情況就會錯。此題選項若將(4)(5)置前不知是否對考生有幫助。
剛看到此題時,就覺得考生作答情形一定不妙。若對線性獨立概念熟悉的學生了解題目的本意作答起來應該沒問題;不過對它不熟悉的學生很可能連題目問什麼都不知道。結果本題確實是多選題中得分率最低的。從下面選項分析來看,每個選項被圈選的比率都達一半以上,考生應是是猜答的居多。
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | *57 | 51 | 50 | *62 | *50 |
| H | 0 | 75 | 40 | 32 | 68 | 53 |
| L | 1 | 41 | 61 | 65 | 58 | 50 |
行列式是否等於$0$與向量是否線性獨立有關。我們先用線性獨立的觀點看這個問題。選項(1)假設兩向量垂直,所以是線性獨立的,因此行列式不為$0$,正確。選項(2)即使 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 是平面 $z=0$ 上的兩平行向量,當然一樣可找到不在平面 $z=0$ 的向量與它們垂直所以此選項錯誤。選項(3)$\displaystyle\overset{\rightharpoonup}{w'},\overset{\rightharpoonup}{w}$ 外積不是零向量,表示它們不平行但又同時與$\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$垂直,所以$\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$一定平行,也就是說行列式為$0$,此選項錯誤。選項(4)由假設空間中所有向量皆可表為 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v},\overset{\rightharpoonup}{w}$ 的線性組合知 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v},\overset{\rightharpoonup}{w}$ 為線性獨立,所以 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 不平行,行列式不為 $0$,選項正確。選項(5)假設 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 不平行,而 $\overset{\rightharpoonup}{w}$ 與它們都垂直,所以 $\overset{\rightharpoonup}{w}$ 不會是平面 $z=0$ 上的向量,因此這三個向量是線性獨立,故得矩陣 $A$ 的行列式不為 $0$,此選項正確。
因為高中課程並未對線性獨立的概念有太多著墨,如何讓學生了解此題的評量重點有點難度,還好談的是二階行列式,學生應可以用平行的概念處理。先讓學生了解,整題主要評量的是若 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 這兩個在平面 $z=0$ 的向量是平行的,則可有許多不平行的向量同時與 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 垂直,而若 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 不平行,則僅有與向量 $(0,0,1)$ 平行的向量會同時與 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 垂直。接下來比較難的便是邏輯問題了,也就是對於「若...則...」這樣的敘述方式是否了解。例如選項(2)、(3)談的都是假設有與 $(0,0,1)$ 不平行的向量同時與 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 垂直,所以 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 必需平行。選項(5)由 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 不平行知 $\overset{\rightharpoonup}{w}$ 必為 $(0,0,t)$ 其中 $t\ne0$ 所以 $A$ 的行列式為 $t\left|\begin{array}{cc} a & b \\ b & a \end{array}\right|$,故不為 $0$。比較難的還是選項(4),因為由假設可知 $t\ne 0$,否則三個向量都在平面 $z=0$ 上,無法表示所有坐標空間的向量,但是知道 $t\ne 0$ 後,可能因當初處理選項 (2)時知道 $t\ne 0$ 未必可推得行列式$\left|\begin{array}{cc} a & b \\ c & d \end{array}\right|\ne 0$,因此反而沒有選這個選項。事實上此選項的題設比選項(2)的題設 $t\ne 0$ 條件強得多。即使 $t\ne0$ 但 $\overset{\rightharpoonup}{u},\overset{\rightharpoonup}{v}$ 平行,仍無法表示所有坐標空間的向量。總之,這個地方,維度的概念仍是需要的。
前4個選項還好,最後一個選項相信許多考生會列式但覺得計算複雜。這次考題大家喊計算複雜,這個選項應該是其中之一。看看選項分析,令人訝異的是選項(4)答得很好,表示考生大多有對稱的概念;不過類似概念的選項(3)卻有超過一半的考生誤選,考生作答的狀況實在難以理解。
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | *61 | 30 | 54 | *72 | 47 |
| H | 0 | 79 | 13 | 44 | 80 | 38 |
| L | 1 | 40 | 48 | 63 | 64 | 55 |
在此想談談選項(5)這個複雜的計算,除非見過,要在考場上臨時想到什麼快速的方法計算,實非易事。不過在講解時,不妨花一點時間討論一下它的計算,讓學生對二項式的性質有更進一步的了解。我們從算 $E(X_1),E(X_2)$ 開始談。只投一次,期望值為 $\frac{1}{2}\times 5+\frac{1}{2}\times 7=6$。因為對稱的關係,這正是投一正面,一反面所得數字的平均數。投兩次的話,期望值為 $\displaystyle C^{2}_{0}(\frac{1}{2})^2\times(2\times 5)+C^{2}_{1}\times(\frac{1}{2})^2\times 12+C^{2}_{2}(\frac{1}{2})^2\times (12-2\times5)$。由於二項式係數的對稱性(即 $C^{2}_{0}=C^{2}_{2}$)以及投兩次正面,兩次反面所在時鐘位置的對稱性(即 $10$ 和 $2$ 的平均數為 $6$)我們可以把此期望值整理成 \[\left(C^{2}_{0}(\frac{1}{2})^2\times6+C^{2}_{1}\times(\frac{1}{2})^2\times 6+C^{2}_{2}(\frac{1}{2})^2\times6\right)+C^2_1\times(\frac{1}{2})^2\times 6=6(\frac{1}{2}+\frac{1}{2})^2+3=9.\]注意中間項,即一正一反的情況所在位置是 $12$ 比平均數多 $6$,所以為了湊二項式,就把這部分 $C^2_1(\frac{1}{2})^2\times 6$ 提出來。現在應該大概知道怎麼回事了。 同樣的投三次,期望值為 $C^3_0(\frac{1}{2})^3\times2+C^3_1(\frac{1}{2})^3\times 5+C^3_2(\frac{1}{2})^3\times7+C^3_3(\frac{1}{2})^3\times10$。一樣用對稱性知會等於 $C^3_0(\frac{1}{2})^3\times6+C^3_1(\frac{1}{2})^3\times 6+C^3_2(\frac{1}{2})^3\times6+C^3_3(\frac{1}{2})^3\times6=6(\frac{1}{2}+\frac{1}{2})^3=6$。
從這裡我們可歸納出,當投擲 $n$ 次,若 $k\ne\frac{n}{2}$,則由於投出 $k$ 次正面($n-k$次反面)與投出 $k$ 次反面($n-k$次正面)其機率相同,且二者所在時鐘位置的平均值為 $6$ 故在計算期望值中此二項的值會等於 $C^{n}_{k}(\frac{1}{2})^n\times6+C^{n}_{n-k}(\frac{1}{2})^n\times6$。因此當投擲次數為奇數時,期望值為 $6$;而當投擲次數為偶數 $2m$ 時,投擲$m$次正面,$m$次反面的情況在計算期望值時此部分的值為 $C^{2m}_{m}(\frac{1}{2})^{2m}\times(12)$,故可推得期望值為 $6(\frac{1}{2}+\frac{1}{2})^{2m}+C^{2m}_{m}(\frac{1}{2})^{2m}\times6$。 也因此我們算得 $E(X_8)=6(1+C^8_4(\frac{1}{2})^8)$。
一般複數的題目大都表現不好,這次也不例外。選項分析中可看出,除了選項(1)代值檢查的簡單問題外,其他錯誤的選項都有近六成的考生圈選。依然是猜答的成分居多。| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | 27 | *69 | *57 | 57 | 60 |
| H | 1 | 15 | 84 | 57 | 41 | 56 |
| L | 1 | 42 | 56 | 57 | 67 | 60 |
講解此題時老師可以讓學生試著用 $z=a+bi$ 代入解 $a,b$ 的方式處理看看,讓學生理解像這類僅牽涉乘法與共軛的複數問題,用極式處理的好處。選項中提及絕對值與主輻角就是提醒考生用極式處理。但考生表現仍不佳,可見大多數學生對極式的運算很不熟悉。會拿此題出來探討,主要還是看到選項(5)連前$33\%$的高分組考生都有近六成圈選,實在令人訝異。高分組中有近六成的考生選擇選項(3),表示他們知道若 $\alpha$ 滿足式子,則 $i\alpha$、$i(i\alpha)=-\alpha$ 以及 $-i\alpha$ 都會滿足。那麼為何選項(5)還有同樣比率的考生覺得僅有 $3$ 個非零複數會滿足式子呢?難不成他們是被代數基本定理誤導,以為這是三次多項式所以會有三個複數根。但若真是如此,那麼 $0$ 也是一個解,不就應該僅有兩個非零複數會滿足啊?不管如何,老師應該可以在此讓學生知道 $z^3-4i\overline{z}$ 並不是一個複係數的多項式。因為式子裡有 $\overline{z}$,沒有一般多項式的除法原理,所以無法套用代數基本定理。最簡單的例子就是 $z-\overline{z}$,雖然 $z$ 僅有一次,但所有實數都滿足 $z-\overline{z}=0$,所以它有無窮多解。另一方面 $z\overline{z}=-1$,就沒有任何複數會符合,所以無解。
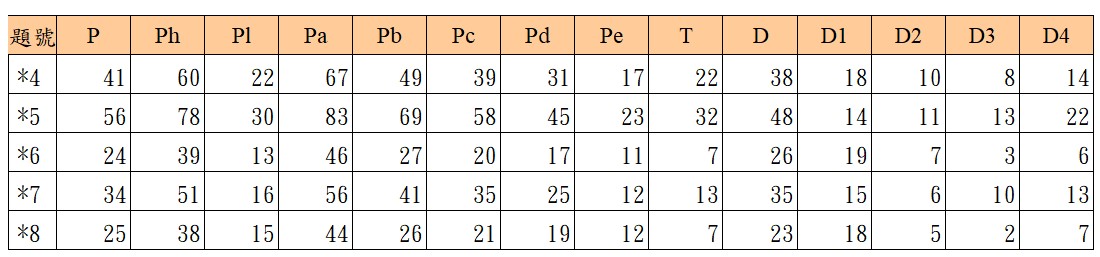
選填題由於猜答不易,得分率往往相對偏低。依大考中心的分類,第10題為中偏難,其餘兩題視為難,尤其第11題答對率僅$2\%$,真的令人吃驚。我們大致談一下這兩個難題。首先,考生成績的 PD 值如下:

直角因為有很好的幾何性質,所以此題作法還蠻多的。不過也因為有很多性質好用,學生反而不知要用哪一個,而不知所措。其實看到直角,也可鼓勵學生用坐標試看看。坐標的代數做法較直接,比較沒有幾何不知用那個方法的困擾。不過用坐標處理問題,一定要鼓勵學生適時使用向量這個工具,而不是只有點,直線這樣的概念。或許是108課綱把坐標平面上的直線與圓和向量分在不同學年,學生較難將兩者連結。這兩年下來,發現學生在處理點、線問題時還是習慣使用高一的方法,而不知很多情況用向量的看法更好處理。
此題如何架坐標呢?由於 $\angle C$ 是直角,當然是把 $C$ 點視為原點。然後依個人喜好定 $A$ 點、$B$ 點那個在 $x$ 軸、$y$ 軸。讓我們定 $A,B$ 的坐標分別為 $(0,\sqrt{3})$, $(2,0)$。接下來的工作就是找到 $M, N$ 兩點的坐標了。先找 $N$,因為 $\triangle ANC$ 是頂角為 $120^\circ$ 的等腰三角形,$N$ 到底邊 $\overline{AC}$ 的高在 $\overline{AC}$ 的中垂線上且長度為 $\displaystyle\frac{\sqrt{3}}{2}\tan30^\circ=\frac{1}{2}$。所以我們只要在 $\overline{AC}$ 的中點 $(0,\frac{\sqrt{3}}{2})$ 往 $\triangle ABC$ 的外部,沿著與 $\overset{\rightharpoonup}{CA}=(0,\sqrt{3})$ 垂直的方向移動 $\frac{1}{2}$ 的距離,即向量 $(-\frac{1}{2},0)$,就可得到 $N$ 點坐標 $(-\frac{1}{2},\frac{\sqrt{3}}{2})$。同理,在 $\overline{AB}$ 的中點 $(1,\frac{\sqrt{3}}{2})$ 往 $\triangle ABC$ 的外部,沿著與 $\overset{\rightharpoonup}{AB}=(2,-\sqrt{3})$ 垂直的方向移動 $\frac{\sqrt{7}}{2\sqrt{3}}$ 的距離,即向量 $\frac{1}{2\sqrt{3}}(\sqrt{3},2)$,就可得到 $M$ 點坐標 $(\frac{3}{2},\frac{5\sqrt{3}}{6})$。
每次都不太想談排列組合的問題,不過後來都有某些原因(大多是答對率太低)不得不談。這次還是無法例外,答對率 $2\%$,真是太可怕了。沒有拿出來關心一下好像很不應該。不知這是否是歷年來答對率最低的一題,不過真的參不透為什麼會這麼低。 或許是本卷計算太多,大部分考生沒有充分時間處理這一題。但也有人認為,題目的情境是機率,但最後問的竟是排列,處理方式策略不同當然影響答對率。個人也覺得這個因素影響頗大。畢竟處理機率問題很少會分成兩個樣本空間處理,而這題的排列問題分成從9張牌抽(8僅有一張)和從10張牌抽(兩個8同時出現)兩種情況處理會容易多了。當然了本題答對率這麼低真正的因素很難斷定,但個人還是認為數學歸數學,減少不必要的情境干擾比較好。
回來談題目數學本身。本題談的是“或”的問題,也就是滿足條件(1)或條件(2)的排列有幾種。這樣的問題比較難,由於一般來說“且”比較好算(畢竟個數比較少),所以通常我們會用“取捨原理”(這是課綱的說法,我習慣用“排容原理”)來處理“或”的問題。也就是說若符合條件(1)的集合為 $A$,符合條件(2)的集合為 $B$,則符合條件(1)或條件(2)的個數應為 $\#(A)+\#(B)-\#(A\cap B)$。不過本題在策略上計算 $A$ 的個數時有點複雜(其實牽涉到處理 $A\cap B$),所以應該換一個角度思考。常常建議老師教導排列組合問題時,讓學生學習到“分類”的概念。多嘗試幾種不同的分類方式,讓學生了解如何找到好的分類。分類就是將集合分割成不相交的情況,其實意味著避免用到“取捨原理”。例如本題在處理時分類成有兩個 $8$ 和 沒有兩個 $8$ 兩類,就容易多了。事實上我們是將 $A\cup B$ 分割成 $A\setminus (A\cap B)$(即 $A$ 扣掉 $A\cap B$ 的部分)以及 $B$ 兩部分,就可以各別算它們的個數加起來得到答案了。此題 $B$ 的部分原本就好算,而 $A\setminus (A\cap B)$ 也是大家熟悉的從 $1,2,\dots,9$ 這九張牌中,排出大於 $6400$ 的個數。總之,別忘了在處理“或”的問題時還有這一招。
今年手寫題的表現,依然令人心寒。大家都說今年計算複雜,但是沒有親自閱卷實在無法體會,很大部分考生千奇百怪的計算錯誤。撇開後面確實較複雜的計算,連 12 題正確計算的考生已經不多了。
我們就談談 12, 13 題閱卷時看到的情況。其他題目也是一些程序性的問題(答題的考生就更少了),就不多談了。
在計算 $\overset{\rightharpoonup}{CO}$ 與 $\overset{\rightharpoonup}{CP}$ 夾角的餘弦值,就改到數量頗驚人的卷子在計算 $\overset{\rightharpoonup}{CO}$ 與 $\overset{\rightharpoonup}{CP}$ 的內積時就出錯了,更別說還要接著計算 $\overset{\rightharpoonup}{CO}$ 與 $\overset{\rightharpoonup}{CP}$ 的長度,最後還有一個除掉長度乘積的計算,能正確計算此餘弦值的考生已經不多了。更訝異的是有相當多的考生是用餘弦定理處理此餘弦值的,除了計算稍微複雜外,題目已用向量表達,學生避開向量處理,很難理解其背後因素。是否與我前面所提,將平面坐標圓與直線單元與向量單元分成不同學年,造成缺乏這方面整合的能力。這在第 13 題就更明顯了。處理 $y=f(x)$ 在 $P$ 點的切線 $L$ 後,接下來只要說此直線 $L$ 也是圓 $\Omega$ 在 $P$ 點的切線。圓心 $C$ 到 $P$ 點所形成的向量 $\overset{\rightharpoonup}{CP}$ 剛才已經知道了,不就說明 $\overset{\rightharpoonup}{CP}$ 與 $L$ 垂直即可?不過見到絕大多數的解法是用了一些(各式各樣)不知那裡學到的切線公式。當然在這裡並不是要去區分哪一種解法好,不過108課綱在條目 G-11A-1 平面向量單元備註上提及:「請注意連結 10 年級所學的基礎」,若老師能在此單元中幫學生將過去圓與直線相關問題相連結,應能讓學生對向量的用處有更進一步的認識。