
第一次的分科數乙,大家普遍認為簡單。從公佈頂標的原始成績來看,維持在過去數乙的85分上下(過去僅最難的104數乙落在69,以及109數乙落在77)。若整體學生程度變化不大,與往年相較並不能算是特別簡單(106數乙頂標高達92)。依照大考中心難易度分類,此次除了手寫題外,選擇(填)的14題中:易的題目(答對率 $\ge60\%$)有7題;中偏易的題目(答對率 $59\%\sim45\%$)有3題;中偏難的題目(答對率 $44\%\sim30\%$)有3題;難的題目(答對率 $\lt30\%$)有1題。其實本試卷,相對來說還是有一些難題,不過由於題目的設計與編排讓它變簡單了。老師在講解題目時,仍建議不要只以答對這些題目為目標,而是儘量探討讓學生理解題目背後的原理,以免稍微更動一下題目,就不會做了。
解析:循環小數的運算,應屬評量數乙無窮等比級數單元。事實上只要知道循環小數的分數表法 $0.{\overline 5}=\dfrac{5}{9}$ 就可得所求為 $5+\dfrac{25}{9}=7+\dfrac{7}{9}=7.\overline{7}$,也不必真正了解無窮等比級數。比起 數乙參考試卷(二)的第1題 應是容易許多。
本題全體的答對率(P)為 $77\%$ 為全卷第二高(僅次於第16題),不過前 $33\%$ 的答對率(Ph)為 $97\%$ 是全卷最高的。從鑑別度中可看出 D4 為 39,也就是說考生中原始成績後 $21\%\sim40\%$ 的答對率(Pd)高出後 $20\%$ 的答對率(Pe)多達 $39\%$。也就是說本題很明確地鑑別出這兩群的考生。從選項分析大約可以看出後 $33\%$ 的考生對於本題的作答情況。
大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 77 | 97 | 47 | 98 | 95 | 88 | 72 | 33 | 50 | 3 | 7 | 16 | 39 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | 15 | 4 | *77 | 3 | 1 |
| H | 0 | 2 | 1 | 97 | 0 | 0 |
| L | 0 | 36 | 9 | 47 | 5 | 3 |
從選項分析可以看到後$33\%$的低分組(L)選答選項(1)高達$36\%$。也就是說他們“偷懶”無視「循環」符號直接將 $1.5$ 乘上 $5$(若勤勞一點多寫一位 $1.55\times5=7.75$ 說不定就答對)。對於不想記憶循環小數分數表法的學生,或許可以鼓勵他們回歸處理等比級數的方法,即乘上公比 $r$ 或 $\dfrac{1}{r}$ 再相減消去共同項。例如本題可設 $S=1.\overline{5}\times5$,因此乘上 $10$(若循環節為$n$則乘$10^n$)得 $10S=15.\overline{5}\times5$。相減得 $9S=14\times5$,再直接將$70$除以$9$,就能得到 $S=7.\overline{7}$。若學生喜歡純數字操作,要他們理解由於乘法計算一般都是從最低位數開始,所以遇到循環小數(尤其循環節長的情況)通常不能直接用乘法處理。不過若是乘上 $10$、$100$ 這種乘上 $10^n$ 的情形,就可以用進位處理。至於除法(這裡指的是除以有限小數),由於計算都是從最高位數開始,所以便可直接處理。例如本題由於剛好是循環小數乘以 $5$,我們再多乘以 $2$,就可以進位得到 $15.\overline{5}$(因為總共乘以 $10$)。最後再直接用除法將 $2$ 除回去,得到 $7.\overline{7}$。
解析:此題僅評量圓方程式,以及方程式圖形上的點之意義。選項(1)就是正確答案,很難理解為何答對率僅 $60\%$。選項中僅有3個是圓,即使不知其餘一個橢圓、另一個是拋物線(不屬數乙課程),仍令人不解為何不選選項(1)。從選項分析可看出前 $33\%$ 的高分組(L)有 $7\%$ 選擇選項(2),而低分組(L)最多人選這個選項。是否誤解圓指的是圓的內部?不管如何,坐標平面上一個方程式的圖形指的是「符合此方程式的點坐標所成的圖形」,這一點務必要讓學生理解。如此學生應該就能理解為何半徑為 $r$ 的圓其方程式一定可寫成 $(x-a)^2+(y-b)^2=r$ 這樣的形式且圓心 $(a,b)$ 不符合此方程式,所以不在此方程式的圖形上。
大考中心提供的答對率、鑑別度分組資料如下:| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60 | 91 | 25 | 95 | 84 | 64 | 39 | 18 | 66 | 11 | 20 | 25 | 21 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | *60 | 19 | 7 | 5 | 9 |
| H | 0 | 91 | 7 | 1 | 0 | 0 |
| L | 0 | 25 | 27 | 14 | 12 | 21 |
解析:評量條件機率的問題。原本要計算“A大於B”以及“B為6且A大於B”這兩個事件的元素個數,屬於有系統的計數單元;不過出題者善意地利用列表方式顯示了各種情況的大小關係,所以嚴格來說本題僅評量條件機率的定義。也就是說若令「A大於B」的事件為$S$以及,「B為6」的事件為$T$,則在“A大於B”的條件下,“B為6”的條件機率為$\dfrac{p(S\cap T)}{p(S)}$。因為題目說兩個骰子是公正的,所以樣本空間中每個元素發生的機率皆相同,因此我們只要算出$S$的元素個數為$18$,$S\cap T$的元素個數為$2$,就可算出答案為 $\dfrac{1}{9}$。
本題答對率僅$65\%$可見許多學生對條件機率定義仍不清楚。從選項分析中可以看出後$33\%$的低分組(L)考生,大多數(占$46\%$)選擇了選項(4) $\dfrac{1}{18}$(即$p(S\cap T)$)。這也應驗了一般認為學生對於「在$S$的情況下,發生$T$的條件機率」以及「$S$與$T$同時發生的機率」,兩者容易混淆的說法。 講解時建議可以利用題目列表的機會,也讓學生計算在“B為6”的條件下,“A大於B”的條件機率。應能讓學生更清楚“條件機率”和“且”之不同。 大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 65 | 95 | 29 | 98 | 88 | 72 | 48 | 19 | 66 | 10 | 16 | 24 | 29 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | 5 | *65 | 4 | 24 | 1 |
| H | 0 | 1 | 95 | 0 | 4 | 0 |
| L | 0 | 10 | 29 | 11 | 46 | 4 |
老師講解此題時,建議不要列表,直接問條件機率為何。有系統的計數這個單元,原本就是希望學生能善用分類的方式計數。可利用本題讓學生了解如何善用好的分類方式在計數上。由於題目要算與B有關的機率,本題自然是利用B來分類較為方便(即表中以列來計數)。當然了,本題樣本空間中每個元素發生機率相同才可簡化成計數問題。我們也可同此題列表,但考慮的是不公正的骰子,給予各點數發生的機率,最後問同樣的問題以評量更進一步機率的概念。
解析:或許此題可歸類於評量空間概念,但相信許多考生不理解這一題在考什麼。 主要是較難和高中學習內容條目相呼應,考生很可能不知如何處理本題。應該算是純粹數學素養的問題,題目所探討的問題個人認為是本卷最難的一題。不過因為安排在單選題讓問題受限,再加上題目敘述上,容易讓考生直觀(但未必正確)就能選到正確的選項,使得本題達到單選題最高的答對率($78\%$)。由於無從判斷考生對此題的理解程度,這裡就不列出鑑別度與選項分析。
原題若改問與點 $A$(或其他頂點)距離最遠的頂點,可能較能達到原本想評量的目的。在此我們故意去掉題目中 “$\overline{OG}\gt1$” 的假設,探討依題意對頂點依序標號所有的可能性。為了不涉及正立方體的轉動,我們固定此正立方體以及其中一個頂點 $O$,想要了解依題意對頂點依序標號的方式,到底距離點 $O$ 最遠的頂點有哪些可能的標號?總共會有幾種標號的方法?如此一來,這是屬於“有系統計數”的問題,我們可以用適當的分類來處理此問題。首先注意由於 $\overline{OA}=1$,點 $A$ 必需與點 $O$ 相鄰。同理,點 $B$ 必需與點 $A$ 相鄰。換言之 $A$、$B$兩點會和點 $O$ 在此正方體的同一面上。因此我們可以將問題分成點 $C$ 與 $O,A,B$ “不共面” 以及 “共面” 兩種情況來討論。
我們也可用坐標方式探討這個問題。為了方便起見,可設頂點 $O$ 的坐標為 $(0,0,0)$,且與 $O$ 相鄰的頂點坐標分別為 $(1,0,0)$、$(0,1,0)$、$(0,0,1)$。應該不難理解相鄰的兩個頂點其坐標會差 $\pm(1,0,0)$、$\pm(0,1,0)$ 或 $\pm(0,0,1)$。換言之,相鄰的兩個頂點其坐標 $(a,b,c)$ 三個位元之和 $a+b+c$ 奇偶會相異。也因此,依題意 $O,A,B,C,D,E,F,G$ 依序相鄰且原點 $O$ 其坐標的三個位元之和是 $0$ 為偶數,可知點 $A,C,E,G$ 三個位元之和應為奇數;而點 $B,D,F$ 三個位元之和應為偶數。但坐標為 $(1,1,1)$ 的頂點距離原點 $O$ 最遠,且其坐標三個位元之是奇數 $3$。因此除了點 $A$ 確定與 $O$ 相鄰外,其餘三點 $C,E,G$ 皆有可能標示為與點 $O$ 最遠的點。這和剛才用幾何探討的結果相吻合。
解析:此題探討將二維數據變換對迴歸直線的影響。114學測數A第12題也探討相關問題,不過該題複雜多了。本題除了情境有點奇怪外,在數學上充分評量了迴歸直線重要的基本概念。不過在考場上為了保險起見,因為數據量不大,應該有許多考生不顧前面的資訊,直接算迴歸直線吧!浪費了出題者善意的鋪陳,有點可惜。 本題答對率 $34\%$ 和預期相當。雖不是全卷答對率最低的一題,不過前$33\%$的高分組答對率(Ph)為 $48\%$,是這一組(H)全卷答對率最低的一題。甚至細分到前$20\%$最高分組也發生同樣情況,答對率(Pa)$59\%$ 也是全卷最低的。可見本題是本卷鑑別高分群的重要題目。 大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 34 | 48 | 26 | 59 | 30 | 27 | 28 | 24 | 22 | 19 | 3 | -1 | 4 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | 27 | 15 | *34 | 18 | 6 |
| H | 0 | 30 | 6 | 48 | 13 | 3 |
| L | 0 | 19 | 26 | 26 | 20 | 9 |
從選項分析中可以看出前$33\%$的高分組(H)考生,有 $30\%$ 選擇了選項(1)。可見高分組考生有認真看題目,但被誤導以為資料重排不會改變迴歸直線(大部分的低分組為何沒有被誤導?)。 要注意,這裡的重排不是每組 $(x,y)$ 一起重排;而是將 $x$、$y$ 拆開各自重排(雖然不大理解這樣重排的意義何在,不過我們只關心這裡的數學問題)。因為 $x$、$y$ 的相關性已經改變,迴歸直線應該也會改變。事實上重排的方式是將 $x$、$y$ 分別以遞增的方式重排,一般來說會增強 $x$、$y$ 的相關性。也就是說很可能相關係數會更接近 $1$,也因此比較可能的是新的迴歸直線斜率會大於原來的斜率 $\dfrac{5}{4}$。我們具體求證一下。為了方便起見,令原來的二維數據為 $(x_i,y_i)$;而新的數據為 $(x_i',y_i')$。因為一維數據重排不會影響平均數,所以我們有 $\mu_x=\mu_{x'}$ 以及 $\mu_y=\mu_{y'}$。也因此標準差也不會改變,亦即 $\sigma_x=\sigma_{x'}$ 以及 $\sigma_y=\sigma_{y'}$。因為新舊資料的迴歸直線斜率分別為 $r_{x,y}\dfrac{\sigma_y}{\sigma_x}$ 以及 $r_{x',y'}\dfrac{\sigma_{y'}}{\sigma_{x'}}$,所以我們只要比較兩組資料的相關係數 $r_{x,y}$ 和 $r_{x',y'}$ 的大小關係即可。 從相關係數 \[r_{x,y}=\frac{1}{8\sigma_{x}\sigma_{y}}\left(\sum_{i=1}^8x_iy_i-8\mu_x\mu_y\right),\quad r_{x',y'}=\frac{1}{8\sigma_{x'}\sigma_{y'}}\left(\sum_{i=1}^8x'_iy'_i-8\mu_{x'}\mu_{y'}\right)\] 我們可以看出 $x$、$y$ 拆開各自重排確實會改變相關係數,而且比較 $r_{x,y}$ 和 $r_{x',y'}$ 的大小,僅需比較 $\displaystyle\sum_{i=1}^8x_iy_i$ 和 $\displaystyle\sum_{i=1}^8x'_iy'_i$ 即可。而比較新舊兩組資料可發現相異的數據分別為 $(x,y):(3,5),(4,4),(5,8),(8,7)$ 以及 $(x',y'):(3,4),(4,5),(5,7),(8,8)$。所以由 $3\cdot5+4\cdot4+5\cdot8+8\cdot7=127$ 小於 $3\cdot4+4\cdot5+5\cdot7+8\cdot8=131$,可得 $r_{x,y}\lt r_{x',y'}$,也因此知 $m\gt\dfrac{5}{4}$。最後由於兩條迴歸直線都會通過在第一象限的點 $(\mu_{x},\mu_{y})=(\mu_{x'},\mu_{y'})$ 且新的迴歸直線斜率比較大,因此其 $y$ 截距 $b$ 會小於舊的迴歸直線的 $y$ 截距 $-\dfrac{1}{4}$。
解析:評量 $\Sigma$ 符號以及對數性質。只要熟悉,應該就能處理。整體答對率為 $56\%$。不過高分組答對率(Ph)為 $91\%$ 和第二題相同。整題答對率會低於第二題就是因為低分組答對率降低,這一方面應再加強。本題稍未注意底數不同或忘了符號,會誤選選項(1)、(5)。從選項分析來看,高分組僅有少數掉入陷阱。不過低分組考生最多數(占$34\%$)選擇了選項(3),實在令人不解。大考中心提供的選項分析如下:
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | 8 | 7 | 16 | *56 | 13 |
| H | 0 | 4 | 0 | 0 | 91 | 3 |
| L | 1 | 10 | 17 | 34 | 20 | 19 |
雖然對數有其方便性,但若學生對指數較熟悉,依然可鼓勵他們利用指數來處理對數問題。本題可令 $\displaystyle a=\sum_{k=1}^5\log_7\frac{2k-1}{2k+1}$,得 $7^a=\dfrac{1}{3}\times\dfrac{3}{5}\times\cdots\times\dfrac{9}{11}=\dfrac{1}{11}$。再取常用對數得 $a\log7=-\log11$。
解析:本題只是二階方陣的運算,雖然問題牽涉到一些運算的性質,不過直接計算也花不了太多時間。至少前三選項應該很快的可以作答,從選項分析來看前$33\%$的高分組(H)這幾個選項答得不錯;不過選項(2)簡單的加法對於後$33\%$的低分組(L)竟然有四分之一的考生答錯。大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 67 | 96 | 30 | 98 | 91 | 78 | 48 | 21 | 55 | 66 | 7 | 13 | 30 | 27 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | *83 | *90 | 17 | 22 | *70 |
| H | 0 | 99 | 100 | 1 | 3 | 94 |
| L | 0 | 62 | 76 | 42 | 48 | 41 |
從答對率的資料來看,此題的全對率(T)僅$55\%$也不盡理想。或許許多考生覺得計算有點多,而跳掉一些選項吧!在此,我們利用方陣的運算性質來探討減少一些計算。首先二階方陣加法有結合律 $(A+B)+C=A+(B+C)$ 和交換律 $A+B=B+A$。注意因為有結合律,所以一般來說三個以上的方陣加法都不寫括號。而乘法也有結合律 $A(BC)=(AB)C$(本題因為只談兩矩陣相乘所以不需用到結合律);但沒有交換律。至於加法與乘法之間,仍然有分配律。所以本題 中 $(A+B)^2$,因為沒有乘法交換律,利用分配律僅能寫成 \[(A+B)^2=(A+B)(A+B)=A(A+B)+B(A+B)=A^2+AB+BA+B^2.\] 同理知 $(A-B)^2=A^2-AB-BA+B^2$。故本題我們僅要計算 $A^2,AB,BA,B^2$ 就可回答所有問題。直接計算得 $A^2=A$, $AB=B$, $B^2=B$ 以及 $BA=A$。因此選項(3)錯誤;選項(5)由 $(A+B)^2=A^2+AB+BA+B^2$ 知其等於 $A+B+A+B=2(A+B)$。選項(4)因為 $(A-B)^2=A^2-AB-BA+B^2$ 會等於 $A-B-A+B$ 為零矩陣,當然不等於 $A^2-2AB+B^2=A+B$。從前面計算可以發現 $A-B$ 不是零矩陣但 $(A-B)^2$ 是零矩陣。所以方陣乘法會有非零矩陣平方後為零矩陣的情況發生。事實上在2階方陣中除了零矩陣外,所有形如 $\begin{bmatrix} a & -\dfrac{a^2}{b} \\ b & -a \end{bmatrix}$ 的矩陣($b\ne0$),都會滿足其平方為零矩陣。
解析:這一題評量鈍角三角形,以及正、餘弦定理。考點很多,對於學生來說,應該是較麻煩的一題。本題全對率(T)僅$13\%$,而高分組(甚至前$20\%$的最高分組),本題答對率在全卷僅高於第5題。一般來說高分組的學生,對於第5題的統計問題較不熟悉,不過對於三角的問題應該不陌生。若再進一步看一下選項分析,每個選項高分組的作答情形都很不理想。是不是因為 $\angle C$ 為 $29^\circ$ 不是特別角,而不知和 $30^\circ$ 作比較?或是將正弦、餘弦遞增遞減情形搞混?會不會是每個選項都是不等式,學生不會分析判斷?這些或許老師們可以多留意了解。大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31 | 54 | 14 | 65 | 36 | 23 | 17 | 13 | 13 | 40 | 29 | 13 | 6 | 4 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | *75 | *51 | 41 | 47 | 40 |
| H | 0 | 93 | 64 | 29 | 23 | 28 |
| L | 0 | 54 | 48 | 56 | 61 | 49 |
前三個選項可以用餘弦定理和正弦定理處理,不過這樣的看法,選項(3)的難度頗高。然而若用以下的圖示,應該很快地看出這三個選項只是評量“鈍角三角形”(為了讓鈍角的效果比較明顯,這裡讓 $\angle A$ 超過 $91^\circ$)。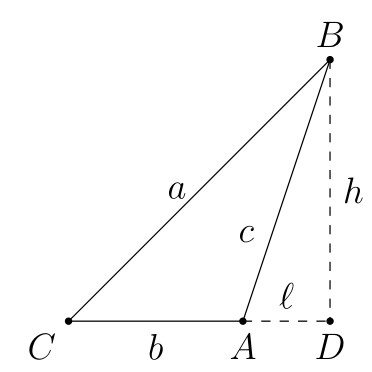 這裡 $D$ 是 $B$ 到直線 $AC$ 的投影。為了方便起見,我們令 $\overline{BD}=h$ 以及 $\overline{AD}=\ell$。由 $\triangle BDA$ 和 $\triangle BDC$ 皆為直角三角形,可得 $a^2=(b+\ell)^2+h^2$ 以及 $c^2=\ell^2+h^2$。所以 $b^2+c^2=b^2+\ell^2+h^2\lt (b+\ell)^2+h^2=a^2$,選項(1)正確。又 $a\sin\angle C=h\lt c$,故選項(2)也正確。而 $a\cos\angle C=b+\ell\gt b$,可知選項(3)錯誤。其實選項(1)和(3)是相關的,如果確認選項(1)(2)是對的,不妨讓學生練習一下用反證法,證明選項(3)是錯誤的。也就是假設 $\dfrac{b}{a}\gt\cos\angle C$ 是對的,利用選項(2)的結論以及 $\sin^2\angle C+\cos^2\angle C=1$,會得到與選項(1)相矛盾的結果。
這裡 $D$ 是 $B$ 到直線 $AC$ 的投影。為了方便起見,我們令 $\overline{BD}=h$ 以及 $\overline{AD}=\ell$。由 $\triangle BDA$ 和 $\triangle BDC$ 皆為直角三角形,可得 $a^2=(b+\ell)^2+h^2$ 以及 $c^2=\ell^2+h^2$。所以 $b^2+c^2=b^2+\ell^2+h^2\lt (b+\ell)^2+h^2=a^2$,選項(1)正確。又 $a\sin\angle C=h\lt c$,故選項(2)也正確。而 $a\cos\angle C=b+\ell\gt b$,可知選項(3)錯誤。其實選項(1)和(3)是相關的,如果確認選項(1)(2)是對的,不妨讓學生練習一下用反證法,證明選項(3)是錯誤的。也就是假設 $\dfrac{b}{a}\gt\cos\angle C$ 是對的,利用選項(2)的結論以及 $\sin^2\angle C+\cos^2\angle C=1$,會得到與選項(1)相矛盾的結果。
或許前三個選項是國中數學,大家比較生疏。選項(4)(5)應該是大家熟悉的餘弦與正弦定理了吧!(別忘了卷末有附這兩個定理公式)很訝異這兩個選項高分組考生答得並不好。看到 $\dfrac{a^2+b^2-c^2}{ab}$ 應該會想到餘弦定理,知道它等於 $2\cos\angle C$。而 $\cos\angle C=\cos29^\circ\gt\cos30^\circ=\dfrac{\sqrt{3}}{2}$ 應該也不難看出吧!同樣的,看到外接圓半徑,應該會想到正弦定理,即半徑等於 $\dfrac{c}{2\sin\angle C}$。而 $\sin\angle C=\sin29^\circ\lt\sin30^\circ=\dfrac{1}{2}$,所以推得 $\dfrac{c}{2\sin\angle C}\gt c$ 應該也非難事。本題很多人注意到 $\angle B=60^\circ$,不過這個訊息應該沒什麼必要。若將 $\angle A$ 改為 $92^\circ$,五個選項的答案還是一樣的。不過我們倒可將 $\angle A$ 改為 $89^\circ$,問問學生這五個選項的答案發生哪些變化。
解析:機率與期望值問題,依過去考生表現一直不盡理想。出題者應該也如此預期,所以將本題置於多選題的最後一題。不過這次考生的表現不錯,全體的得分率達到 $63\%$,從大考中心的標準來看是易的題目。 從各組得分率看,前面較高分各組得分率都比偏易的第7題低了許多(尤其是在前 $20\%\sim60\%$ 的得分率,即 Pb,Pc);不過後面低分的兩組得分率反而比第7題高。所以本題題目的本質上,應該不算容易。由於各選項作答情形沒有太反常的現象,這裡僅列出大考中心提供的答對率、鑑別度分組資料。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 63 | 90 | 36 | 94 | 80 | 65 | 51 | 27 | 45 | 54 | 14 | 15 | 14 | 24 |
本題可以有很多變化,為了探討更一般情況我們令牌子的個數為 $n$,其中有 “大獎” 的牌子個數為 $m$,其餘 $n-m$ 個牌子 “無獎”。為了敘述方便,我們改為兩人依序抽獎:第一人抽獎如同題目的選擇(一),抽獎後牌子不放回 。接著讓第二人抽,所以第二人就如同題目中的選擇(二)。如果主持人沒有動手腳,在第一人抽獎後加牌或減牌,大家應該都知道不管先抽或後抽,抽到大獎的機率都是 $\dfrac{m}{n}$。為什麼呢?第一個抽獎得大獎機率是 $\dfrac{m}{n}$ 沒問題。至於第二個抽獎者,若第一人得獎(已知機率為 $\dfrac{m}{n}$),則第二人得大獎機率為 $\dfrac{m-1}{n-1}$;而若第一人未得獎(已知機率為 $\dfrac{n-m}{n}$),則第二人得大獎機率為 $\dfrac{m}{n-1}$。所以總結第二人得大獎的機率為 \[\frac{m}{n}\times\frac{m-1}{n-1}+\frac{n-m}{n}\times\frac{m}{n-1}=\frac{m}{n}(\frac{m-1}{n-1}+\frac{n-m}{n-1})=\frac{m}{n}.\] 現若如本題,主持人在第一人抽獎後加了一張 “小獎” 的牌子,則第二人抽到大獎的機率會有變化。因為抽到小獎的機率為 $\dfrac{1}{n}$,猜測其餘機率 $\dfrac{n-1}{n}$ 中的 $\dfrac{m}{n}$ 會得大獎,即第二人中大獎的機率應為 $\dfrac{m(n-1)}{n^2}$。讓我們驗證一下:若第一人得獎,則第二人得大獎機率為 $\dfrac{m-1}{n}$;而若第一人未得獎,則第二人得大獎機率為 $\dfrac{m}{n}$。所以總結第二人得大獎的機率為 \[\frac{m}{n}\times\frac{m-1}{n}+\frac{n-m}{n}\times\frac{m}{n}=\frac{m}{n}(\frac{m-1}{n}+\frac{n-m}{n})=\frac{m(n-1)}{n^2}.\] 本題中 $n=5$, $m=2$,故第一人得大獎 $1000$ 元的機率為 $\dfrac{2}{5}$,未中獎得 $0$ 元的機率為 $\dfrac{3}{5}$。也因此第一人所得獎金的期望值為 $1000\times\dfrac{2}{5}=400$ 元。選項(1)正確,而選項(2)錯誤。至於第二人,依前面討論,得小獎 $500$ 元的機率為 $\dfrac{1}{5}$;得大獎 $1000$ 元的機率為 $\dfrac{4}{5}\times\dfrac{2}{5}=\dfrac{8}{25}$;最後未得獎的機率為 $\dfrac{4}{5}\times\dfrac{3}{5}=\dfrac{12}{25}$。因此第二人所得獎金的期望值為 $500\times\dfrac{1}{5}+1000\times\dfrac{8}{25}=420$ 元。選項(4)(5)正確,但選項(3)錯誤。
若題目改成:主持人在第一人抽獎後將剩餘牌子中一張 “無獎” 的牌子取走,這個問題就和有名的「Monty Hall problem」有關。此時第二人抽中大獎的機率便會大於第一人了!原因是:若第一人得獎,則第二人得大獎機率為 $\dfrac{m-1}{n-2}$;而若第一人未得獎,則第二人得大獎機率為 $\dfrac{m}{n-2}$。所以總結第二人得大獎的機率為 \[\frac{m}{n}\times\frac{m-1}{n-2}+\frac{n-m}{n}\times\frac{m}{n-2}=\frac{m}{n}(\frac{m-1}{n-2}+\frac{n-m}{n-2})=\frac{m}{n}\times\frac{n-1}{n-2}\gt\frac{m}{n}.\] 這也是在 Monty Hall problem 中建議換門得到車子的機率比較大的主要原因。
本題還可問一個有趣的問題:主持人應加多少元的牌子,才可讓兩種方法所得獎金的期望值相等?由於第一種方法的期望值為 $400$元,合理的想法應該是加 $400$元的牌子。讓我們回到一般的情況驗證一下。令大獎為 $K$ 元,設小獎為 $x$ 元。則由前面所算的機率可得所得獎金的期望值為 $\dfrac{m(n-1)}{n^2}K+\dfrac{1}{n}x$。令之等於 $\dfrac{m}{n}K$,可得 $\dfrac{1}{n}x=\dfrac{m}{n}(1-\dfrac{n-1}{n})K$,因此解得 $x=\dfrac{m}{n}K$。
解析:評量複數的運算,對於高分組的學生當然沒有問題;但對於低分組的學生就有顯著的差距,使得本題成為整卷鑑別度最高的一題(高達 $88\%$)。從分組鑑別度中可看出 D3 為 42,也就是說考生中原始成績於前 $40\%\sim60\%$ 的答對率(Pc)高出後 $40\%\sim20\%$ 的答對率(Pd)多達 $42\%$。可以說本題很明確地鑑別出這兩群的考生。 大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 55 | 96 | 8 | 98 | 91 | 63 | 21 | 2 | 88 | 7 | 28 | 42 | 19 |
第三種就是利用極式,不過本題不是特別角,也沒有幾何的幫助,這方法應該是自找苦吃。雖然數乙沒有極式,這裡我們還是練習一下。首先將 $1-7i$ 寫成 $\sqrt{50}(\cos\theta+i\sin\theta)$,其中 $\cos\theta=\dfrac{1}{\sqrt{50}}$, $\sin\theta=\dfrac{-7}{\sqrt{50}}$,且將 $-1+i$ 寫成 $\sqrt{2}(\cos\beta+i\sin\beta)$,其中 $\cos\beta=\dfrac{-1}{\sqrt{2}}$, $\sin\beta=\dfrac{1}{\sqrt{2}}$。此時 $\dfrac{1-7i}{-1+i}$ 就可寫成 $\dfrac{\sqrt{50}}{\sqrt{2}}(\cos(\theta-\beta)+i\sin(\theta-\beta))$。利用和角公式 \[\cos(\theta-\beta)=\dfrac{1}{\sqrt{50}}\times \dfrac{-1}{\sqrt{2}}+\dfrac{-7}{\sqrt{50}}\times\dfrac{1}{\sqrt{2}}=\frac{-8}{10},\quad \sin(\theta-\beta)=\dfrac{-7}{\sqrt{50}}\times \dfrac{-1}{\sqrt{2}}-\dfrac{1}{\sqrt{50}}\times\dfrac{1}{\sqrt{2}}=\frac{6}{10},\] 所以 $\dfrac{1-7i}{-1+i}=-4+3i$。
解析:排列組合問題一般來說考生大都表現不佳(尤其放在選填題)。這一題是全卷非手寫題答對率最低的一題並不令人訝異。其實題目並不難,從最高分組(前$20\%$)考生表現來看確實如此,不過次高分組(前$20\%\sim40\%$)的表現落差很大(D1高達36)。本題對這兩組的鑑別度最高,所以程度不錯的學生好好把握“有系統的計數”,才能更上一層樓。確實排列組合的問題有時會牽涉高度技巧性的問題,不過課綱將之定位在“有系統的計數”,也就是只探討能用分類方式處理的問題。所以能掌握如何分類可有效的計算,應該在這個單元都可以有不錯的表現。 本題大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 28 | 62 | 3 | 75 | 39 | 19 | 7 | 2 | 59 | 36 | 20 | 12 | 5 |
題目和實際洗衣機的操作有差異,所以是否操作過洗衣機應與解題沒有太大幫助,還是讀懂題意最重要。基本上是評量「$n$ 個功能可以自由選擇是否開啟」,則由於每個功能有“開、關”兩種選擇且互相獨立所以總共有 $2^n$ 個選擇方式。我們就按照題目程序先按哪種衣料,再選擇模式,最後考慮要開哪些功能。要注意這裡衣料、行程都一定要選一種;然而3種功能是可以隨意選擇要不要開啟(全部不開也可以)。 若照此程序,利用5種布料來分類是合理的。因為選擇“布料一”有限制,其餘布料沒有限制,所以我們可以分成兩類。
我們也可練習一下其他的分類方法。因為模式並沒有任何限制,所以利用模式來分類應該沒有什麼好處。就利用“功能”來分類吧!因為只有功能「A」會因是否開啟影響布料的選擇,所以可用功能「A」是否開啟來分類。
本題可能因為多了“限制”,所以學生較不會處理。一般來說當限制的條件少時,我們也可考慮用扣除的方式處理,不過這裡要注意扣除掉的個數之正確性。從前面討論可以看出這一題中“模式”是來湊熱鬧的(增加格數避免猜答?),我們可以先考慮“布料”、“功能”有幾種選擇即可。若無任何限制,布料、功能總共有 $5\times 2^3=40$ 種選擇。接下來就要扣掉選擇“布料一”且開啟“功能A”的所有選擇。 應該有一些學生會誤以為只有一種。其實題目的例子就已提醒選擇“布料一”且開啟“功能A、B”也要排除。所以要排除的是選擇“布料一”且開啟“功能A”以及所有「B」、「C」兩種功能開啟與否的4種可能。因此“布料”、“功能”總共有 $40-4=36$ 種選擇。最後再乘上“模式”的4種選擇得到答案為 $36\times4=144$。
解析:這是常見的內積問題,不清楚為何會放在選填的最後一題。奇怪的是高分組表現並不很好,但低分組的表現這一題竟是三題選填答對率最高的一題。會不會是有些高分組考生時間不夠,以為選填最後一題較難而未好好作答?而低分組因為題目較熟悉,願意花時間處理?本題和上一題一樣最高分組(前$20\%$)考生表現和次高分組(前$20\%\sim40\%$)的表現差距很大(D1達33)。對這兩組考生的鑑別度很高,所以程度不錯的學生應好好把握這類題型。本題大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 41 | 73 | 16 | 85 | 52 | 34 | 25 | 11 | 57 | 33 | 18 | 9 | 14 |
因為 $A,B,C$ 三點不共線,所以平面上所有向量都可寫成 $\overset{\large\rightharpoonup}{AB},\overset{\large\rightharpoonup}{AC}$ 的線性組合。特別地,$\overset{\large\rightharpoonup}{CB}$ 就可寫成 $\overset{\large\rightharpoonup}{AB}-\overset{\large\rightharpoonup}{AC}$。所以利用內積性質可得 \[\overset{\large\rightharpoonup}{CB}\cdot\overset{\large\rightharpoonup}{AC}= (\overset{\large\rightharpoonup}{AB}-\overset{\large\rightharpoonup}{AC})\cdot\overset{\large\rightharpoonup}{AC}=\overset{\large\rightharpoonup}{AB}\cdot\overset{\large\rightharpoonup}{AC}-\overset{\large\rightharpoonup}{AC}\cdot\overset{\large\rightharpoonup}{AC}=\overset{\large\rightharpoonup}{AB}\cdot\overset{\large\rightharpoonup}{AC}-\overline{AC}^2.\] 因此利用題目已知 $\overset{\large\rightharpoonup}{CB}\cdot\overset{\large\rightharpoonup}{AC}=3$ 以及 $\overset{\large\rightharpoonup}{AB}\cdot\overset{\large\rightharpoonup}{AC}=16$ 推得 $\overline{AC}^2=16-3=13$。這裡應該留意學生可能將 $\overset{\large\rightharpoonup}{CB}$ 寫成 $\overset{\large\rightharpoonup}{AB},\overset{\large\rightharpoonup}{AC}$ 的線性組合時係數正負搞錯。其實平面上所有向量也都可寫成 $\overset{\large\rightharpoonup}{AB},\overset{\large\rightharpoonup}{AC}$ 的線性組合。此時僅要將 $\overset{\large\rightharpoonup}{AB}$ 寫成 $\overset{\large\rightharpoonup}{AC}+\overset{\large\rightharpoonup}{CB}$,就可以利用 $\overset{\large\rightharpoonup}{AB}\cdot\overset{\large\rightharpoonup}{AC}= (\overset{\large\rightharpoonup}{AC}+\overset{\large\rightharpoonup}{CB})\cdot\overset{\large\rightharpoonup}{AC}=\overline{AC}^2+\overset{\large\rightharpoonup}{CB}\cdot\overset{\large\rightharpoonup}{AC}$ 解得 $\overline{AC}^2=16-3=13$。
餘弦定理其實就是內積的性質。若依慣例令 $\overline{BC}=a$、$\overline{AC}=b$、$\overline{AB}=c$,則因 \[a^2=\overset{\large\rightharpoonup}{BC}\cdot\overset{\large\rightharpoonup}{BC}= (\overset{\large\rightharpoonup}{AC}-\overset{\large\rightharpoonup}{AB})\cdot(\overset{\large\rightharpoonup}{AC}-\overset{\large\rightharpoonup}{AB})=\overset{\large\rightharpoonup}{AC}\cdot\overset{\large\rightharpoonup}{AC}-2\overset{\large\rightharpoonup}{AC}\cdot\overset{\large\rightharpoonup}{AB}+\overset{\large\rightharpoonup}{AB}\cdot\overset{\large\rightharpoonup}{AB}=b^2+c^2-2\overset{\large\rightharpoonup}{AC}\cdot\overset{\large\rightharpoonup}{AB},\] 得 $\overset{\large\rightharpoonup}{AC}\cdot\overset{\large\rightharpoonup}{AB}=\dfrac{b^2+c^2-a^2}{2}$,這就是餘弦定理。本題若不喜歡向量運算,就可以直接套用餘弦定理,即 $16=\overset{\large\rightharpoonup}{AC}\cdot\overset{\large\rightharpoonup}{AB}=\dfrac{b^2+c^2-a^2}{2}$ 以及 $-3=\overset{\large\rightharpoonup}{CB}\cdot\overset{\large\rightharpoonup}{CA}=\dfrac{b^2+a^2-c^2}{2}$,相加得到 $13=b^2=\overline{AC}^2$。
解析:因為108課綱將數乙課程加入微積分內容,這是數乙第一次考微積分。從第13題單選的答對率來看,考生表現並不好。從原始成績細分成五組的答對率來看,最高分組(前$20\%$)考生表現和次高分組(前$20\%\sim40\%$)的表現差距很大(D1達31),而次高分組的表現和中間(前$40\%\sim60\%$)的表現差距也很大(D2達32)。可見這題對這三組考生的鑑別度很高。從選項分析來看,低分組最多人(占$42\%$)選擇了錯誤的選項(4),應該是不了解二次微分對圖形凹向的判別。從這裡不難理解在閱卷時發現許多考生誤以為極值發生的點 $-3,1$ 會使得 $f(-3)=f(1)=0$,也有許多誤以為會滿足 $f''(-3)=f''(1)=0$。而誤以為反曲點滿足一次微分為 $0$的情況也不少。也就是說仍有許多學生不是很了解微分基本的意義,一切都僅憑記憶處理。 第13題大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 48 | 85 | 25 | 95 | 64 | 32 | 24 | 26 | 60 | 31 | 32 | 8 | -2 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 2 | 9 | 8 | *48 | 30 | 3 |
| H | 0 | 4 | 1 | 85 | 8 | 1 |
| L | 4 | 7 | 17 | 26 | 42 | 6 |
依題意,$f(x)$ 在 $x=-3,1$ 有極值,故知 $f'(-3)=f'(1)=0$。因為 $f(x)$ 是三次多項式,所以 $f'(x)$ 是二次多項式。因此 $f'(x)$ 可寫成 $a(x+3)(x-1)=a(x^2+2x-3)$。要求出 $f'(x)$,還少一個條件。 若能知道反曲點發生處,就可由 $f'(x)$ 在該處的微分值為 $4$ 解出 $a$。反曲點可由 $f''(x)=0$ 解出,亦即由 $f'(x)=a(x^2+2x-3)$ 得 $f''(x)=a(2x+2)$,解出反曲點發生於 $x=-1$。我們也可由反曲點就是 $y=f(x)$ 的對稱中心,知反曲點會是兩頂點 $(-3,f(-3))$、$(1,f(1))$ 的中點,推得反曲點發生於 $x=\dfrac{-3+1}{2}=-1$(所以反曲點也會發生於二次函數 $y=f'(x)$ 的頂點)。最後由 $f'(-1)=4$,解得 $a=-1$。也因此可得 \[\int_{-3}^1f'(x)\,dx=\int_{-3}^1(-x^2-2x+3)\,dx=-\frac{1}{3}x^3-x^2+3x\Big|_{-3}^1=\frac{32}{3}.\]在113數甲彩蛋我們提供了一個方法,不必求反導函數就可知此定積分為 $\dfrac{1}{6}(1-(-3))^3$。有興趣可按前面連結參考。
應該許多學生仍習慣設 $f(x)=ax^3+bx^2+cx+d$,來解此題。此時由 $f'(x)=3ax^2+2bx+c$ 以及 $f'(-3)=f'(1)=0$ 可得 $27a-6b+c=0$ 且 $3a+2b+c=0$。前面兩式相減得 $b=3a$,因此由 $f''(x)=6ax+2b=6a(x+1)$,得到反曲點發生於 $x=-1$。再由 $f'(-1)=4$ 得 $4=3a-2b+c=-b+c$。又由前 $c=6b-27a=-3b$ 解得 $b=-1,a=-\dfrac{1}{3}$ 以及 $c=3$。最後利用微積分基本定理解得 \[\int_{-3}^1f'(x)\,dx=f(1)-f(-3)=(a+b+c+d)-(-27a+9b-3c+d)=28a-8b+4c=\frac{32}{3}.\]
解析:因為數甲沒有線性規劃,這類問題是數乙獨有,歷年來幾乎是數乙的必考題型。從第16題單選的答對率來看,考生表現不錯。答對率超過 $80\%$ 是全卷最高。從原始成績細分成五組的答對率來看,最低分組(後$20\%$)考生表現和次低分組(後$20\%\sim40\%$)的表現差距很大(D4達36)。這題和第一題一樣有效鑑別出這後兩組考生。第16題大考中心提供的答對率、鑑別度分組資料如下:
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 82 | 96 | 59 | 97 | 94 | 90 | 81 | 45 | 37 | 3 | 4 | 9 | 36 |
學生處理數學問題一直都以為答案正確就可以了,很少仔細寫下過程和原因。然而很多情況雖然答案正確,但得到答案所用的資訊或理由是錯誤的。例如線性規劃問題,使用代頂點方式,很可能可行解區域錯誤,但恰好得到最佳解的頂點正確。為了讓考生理解如何在線性規劃問題呈現正確的過程和原因,往往都會強調正確標示(畫出)可行解區域及其相關資訊。本題組15分中,可行解區域相關的問題佔分就超過10分,所以平時要求學生詳細描述可行解區域中所有的資訊,相當重要。本題有點小陷阱,雖然題目敘述了三個條件,但事實上有四個不等式:$x\le15$、$x+y\le24$、$x\le3y$ 以及 $y\le2x$。其實還有兩個隱含的不等式 $x\ge 0$ 和 $y\ge 0$,不過這裡沒有要求。另外要注意,因為這些條件都要符合,所以這些不等式之間是 “且” 的關係(畫可行解區域要取交集)。應該依規定寫成聯立的形式(這裡因為不想佔篇幅就略去)。
正確畫出可行解區域邊界的直線後,接下來就是要用斜線表示出可行解區域的範圍。若能找到不在邊界但符合條件的點(如 $(5,5)$),則包含該點被直線所圍的區域,就是可行解區域。可惜第16題所找到的點 $(14,10)$ 在邊界上,不過我們知道原點 $(0,0)$ 也符合條件(但還是在邊界上)。由於每個不等式都是半平面,這些半平面的交集會是“凸多邊形”,所以 $(14,10)$ 和 $(0,0)$ 的連線段會在可行解區域內,這樣也可確認可行解區域的範圍。這裡借用大考中心所公佈的評分標準所用的圖: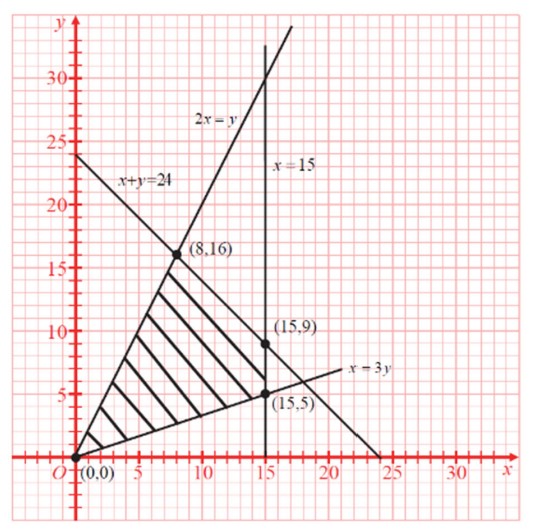 。 對於決定二元一次不等式所決定的半平面,若不想代值判斷也可利用不等式中 $x$ 或 $y$ 的係數來判斷。首先適當的移項,使得不等式中 $x,y$ 的係數至少有一個是正的。若 $x$ 的係數$a$為正,表示越往 $x$ 軸右方其值越大;越往左方其值越小。因此,若不等式為 $ax+by+c\ge0$ 則其表示的區域為直線 $ax+by+c=0$ 的右半(即 $x$ 截距的右方);而 $ax+by+c\le0$ 則其表示的區域為直線 $ax+by+c=0$ 的左半。同理,若 $y$ 的係數$b$為正,則當不等式為 $ax+by+c\ge0$ 時,其表示的區域為直線 $ax+by+c=0$ 的上半(即 $y$ 截距的上方);而 $ax+by+c\le0$ 則其表示區域的為直線 $ax+by+c=0$ 的下半。例如本題中 $x+y\le24$ 所決定的區域,可以選直線 $x+y=24$ 其 $x$ 截距的左方(或 $y$ 截距的下方)。而 $y\le2x$ 可以選直線 $y=2x$ 其 $y$ 截距的下方(或 $x$ 截距的右方)
。 對於決定二元一次不等式所決定的半平面,若不想代值判斷也可利用不等式中 $x$ 或 $y$ 的係數來判斷。首先適當的移項,使得不等式中 $x,y$ 的係數至少有一個是正的。若 $x$ 的係數$a$為正,表示越往 $x$ 軸右方其值越大;越往左方其值越小。因此,若不等式為 $ax+by+c\ge0$ 則其表示的區域為直線 $ax+by+c=0$ 的右半(即 $x$ 截距的右方);而 $ax+by+c\le0$ 則其表示的區域為直線 $ax+by+c=0$ 的左半。同理,若 $y$ 的係數$b$為正,則當不等式為 $ax+by+c\ge0$ 時,其表示的區域為直線 $ax+by+c=0$ 的上半(即 $y$ 截距的上方);而 $ax+by+c\le0$ 則其表示區域的為直線 $ax+by+c=0$ 的下半。例如本題中 $x+y\le24$ 所決定的區域,可以選直線 $x+y=24$ 其 $x$ 截距的左方(或 $y$ 截距的下方)。而 $y\le2x$ 可以選直線 $y=2x$ 其 $y$ 截距的下方(或 $x$ 截距的右方)
本題目標函數為 $P(x,y)=6x+7y$。稱之為目標函數因為它是一個兩個變數的函數。單變數的函數 $f(x)$ 在坐標平面上的圖形 $y=f(x)$ 為一條曲線(包含直線);而兩個變數的函數 $P(x,y)$ 在坐標空間中的圖形 $z=P(x,y)$ 會是一個曲面(包含平面)。本題的函數圖形便是平面 $z=6x+7y$,要求最大值便是要找到可行解區域對應在此平面上其 $z$ 坐標的最大值。有時空間中的函數圖形不好畫,我們可以將平面 $z=k$ 與函數圖形相交的曲線(包含直線)投映在 $xy$ 平面,這就是所謂的「等高線」。利用畫出等高線 $6x+7y=k$ 在可行解區域找到最大、最小值,就是所謂的“平行線法”。對於函數在有界區域的最大最小值,還有一個微積分中常用的方法,也就是找出內部極大、極小值,再和邊界上的點取值比較。因為函數圖形是平面,所以內部不會有極大、極小值,因此線性規劃找最大值還有一個“頂點法”。也就是,比較可行解區域的頂點所代的值即可。
需讓學生確實理解:若用頂點法應將“所有”的頂點列出代值比較,少列一個點或多列出不在可行解區域的點,這樣所得的結論雖然有可能會和代正確頂點的結論一樣,但在數學原理上並不完全正確。所以絕對無法得到完整的分數。本題應列出四個頂點 $(0,0)$, $(15,5)$, $(15,9)$ 以及 $(8,16)$ 且正確代入目標函數得到其值分別為 $0,125,153,160$,才能確認最大值為 $160$(最小值為 $0$)。
若用平行線法,除非等高線與可行解區域的一邊線平行,一般來說僅需代兩點。其中一個會是最大值,另一個是最小值。比起頂點法計算量少,但是務必要說明為何會選這兩點。一個方法就是畫出通過這兩點的等高線,確認此二線沒有“貫穿”可行解區域的內部。例如本題畫出通過 $(0,0)$ 以及 $(8,16)$ 的等高線 $6x+7y=0$ 以及 $6x+7y=160$,確認僅與可行解區域交於一點即可。也可利用斜率說明,例如在 $(0,0)$ 我們發現斜率介於 $\dfrac{1}{3}$ 和 $2$ 之間的直線會穿過可行解區域,而等高線的斜率為 $-\dfrac{6}{7}$,所以僅會交於點 $(0,0)$。在 $(8,16)$ 我們發現斜率大於 $2$ 或小於 $-1$ 的直線會穿過可行解區域,而等高線的斜率滿足 $-1\lt-\dfrac{6}{7}\lt2$,所以僅會交於一點。