一

坐標平面上有兩條拋物線，第一條拋物線的頂點在 (- 4, 0)， 焦點在 (- 4, 4)，第二條拋物線的頂點在 (4, 4)，焦點在 (4, 0)， 求兩條拋物線的交點。

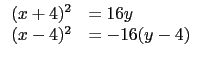
說明:這是一個基本的拋物線問題, 只要了解如何寫下標準形式的拋物線方程式, 再解聯立方程式求交點即可.

要寫下標準式的拋物線方程式第一步就是要先判斷此拋物線的開口方向是上下或是左右, 接著就是求出焦距. 若頂點坐標為 (a, b) 且為開口向上或向下則其方程式為 (x - a)² = 4c(y - b), 其中 c 為焦距. 焦距 c 的絕對值為頂點和焦點距離, 而開口向上時 c 為正; 開口向下時 c 為負. 若頂點坐標為 (a, b) 且為開口向左或向右則其方程式為 (y - b)² = 4c(x - a), 其中焦距 c 的絕對值為頂點和焦點距離, 而開口向右時 c 為正; 開口向左時 c 為負. 因此若知道一標準形式的拋物線的頂點和焦點坐標, 就可以馬上寫下其方程式.

本題第一條拋物線頂點在 (- 4, 0) 而焦點在 (- 4, 4), 由此知焦點在頂點的正上方, 也就是開口向上的拋物線其方程式應為 (x + 4)² = 4cy, 而 c 的絕對值為 (- 4, 0) 和 (- 4, 4) 的距離且 c 為正, 故得 c = 4. 同理知第二條拋物線方程式為 (x - 4)² = 4c'(y - 4), 其中 c' = - 4. 要求此二拋物線之交點即解聯立方程式:

$$\left\{\vphantom{ \begin{array}{rl} (x+4)^2 &=16y\\ (x-4)^2& =-16(y-4)\\ \end{array}%% }\right.$$$$\begin{array}{rl} (x+4)^2 &=16y\\ (x-4)^2& =-16(y-4)\\ \end{array}$$

兩式相加可得 2(x² + 16) = 64, 故得 x = 4 或 x = - 4. 當 x = 4 時代回第一式得 y = 4, 而當 x = - 4 時代回第一式得 y = 0. 故知交點為 (4, 4) 和 (- 4, 0).

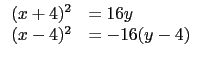
近幾年大考中心數學試題考了幾次二次曲線用定義較容易處理的問題. 基本上那些問題所給資訊較不足, 本題頂點和焦點都給了, 用定義方法處理只不過再推導一次標準型拋物線方程式, 實無必要用定義來解題. 若對用方程式或定義處理二次曲線的適當時機有興趣的同學, 可參考``97 學年指考數學甲''多選題 8 的解說. 本題若硬要和定義扯上, 我們可算出第一條和第二條拋物線的準線分別為 y = - 4 和 y = 8, 而第一條拋物線的頂點 (- 4, 0) 到第二條拋物線的焦點 (4, 0) 的距離和到第二條拋物線的準線 y = 8 的距離皆為 8, 故知 (- 4, 0) 也在第二條拋物線上 (事實上第一條拋物線的頂點為第二條拋物線正焦弦上的一個端點). 同理可得第二條拋物線的頂點也在第一條拋物線上. 由此可得 (4, 4) 和 (- 4, 0) 皆為此二拋物線之交點, 但這並未完整回答這個問題, 因為並未說明不會有其他的交點. 所以我們依然要回歸到解方程式, 說明一個開口向上的拋物線和開口向下的拋物線最多只能有兩個交點, 才算完整回答本題.