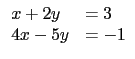
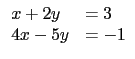
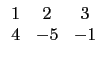
試問下列哪一個選項中的矩陣乘積代表對 A 進行上述步驟?
(1) ![]()
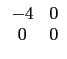
![]()
![]()
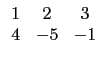
![]() (2)
(2) ![]()
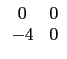
![]()
![]()
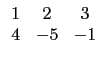
![]()
(3) ![]()
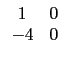
![]()
![]()
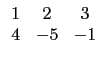
![]() (4)
(4) ![]()
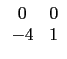
![]()
![]()
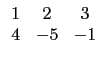
![]()
(5) ![]()
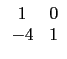
![]()
![]()
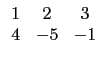
![]()
說明:本題乃將大學線性代數中有關於基本列運算可以表成矩陣的乘法這個事實入題.
不過一般不知道這個性質的同學仍可處理本題,只要利用矩陣的乘法一一驗算即可.
還好這些矩陣的乘法都不複雜, 所以不知道這個性質的同學並沒吃多少虧.
基本列運算可以表成矩陣的乘法這個事實其實很好用,
許多有關於反矩陣的性質都可以由它得到.
所以我們希望利用這個題目來說明一下這個事實. 首先我們令
U = ![]()
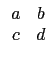
![]() 其中
(a b) 為 U 的第一列, 而
(c d ) 為 U
的第二列. U 是一個 2×2 矩陣, 而題目中的 A 是一個
2×3 矩陣. 我們都知道 U 可以乘在 A 的左邊, 且乘完後 (即
UA) 仍是 2×3 的矩陣 (注意 U 不能乘在 A的右邊).
我們來看看 U 乘在 A 的左邊後會怎麼樣?
其中
(a b) 為 U 的第一列, 而
(c d ) 為 U
的第二列. U 是一個 2×2 矩陣, 而題目中的 A 是一個
2×3 矩陣. 我們都知道 U 可以乘在 A 的左邊, 且乘完後 (即
UA) 仍是 2×3 的矩陣 (注意 U 不能乘在 A的右邊).
我們來看看 U 乘在 A 的左邊後會怎麼樣?
依矩陣乘法定義, 在求 UA 為怎樣的矩陣時, U 的第一列 (是一個
1×2 矩陣) 乘以 A 後會是 UA 這個矩陣的第一列, 而 U
的第二列乘以 A 後會是 UA 這個矩陣的第二列. 所以我們只要知道 U
中每一列乘以 A 後為何, 就可求得 UA. 讓我們來看 U 的第一列
(a b) 乘以 A 後會怎樣. 即,
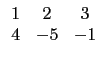 |
= | ||
| = | a |
現在回到我們的問題. 依題意我們希望找到 U 使得 UA 的第一列仍是
A 的第一列所以由上面結果我們知若 U 的第一列為
(a b),
則可令 a = 1 且 b = 0 得到 UA 的第一列仍為
(1 2 3).
同理若 UA 的第二列為 A 的第二列減去 4 倍的 A 的第一列, (即
-4(1 2 3) + (4 - 5 - 1)), 可令 U 的第二列為
(- 4 1). 也就是說若令
U = ![]()
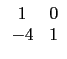
![]() , 則 UA 就是將 A 利用題目所要求的基本列運算所得之矩陣.
至於其他兩種基本列運算, 即某兩列互換以及某一列乘上常數,
相信大家可以如法泡製馬上知道如何得到.
, 則 UA 就是將 A 利用題目所要求的基本列運算所得之矩陣.
至於其他兩種基本列運算, 即某兩列互換以及某一列乘上常數,
相信大家可以如法泡製馬上知道如何得到.
一般來說, 當 A 是一個 m×n 的矩陣. 若要找到一個 m×m
的矩陣 U 使得 UA 就是將 A 做某個基本列運算所得的矩陣,
此時我們只要將 m×m 的單位矩陣做所要求的基本列運算,
這樣所得的矩陣就是所要求的 U 了. 例如本題中我們可將 2×2
的單位矩陣
![]()
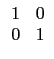
![]() 按照規定的基本列運算 (即第一列不改變, 並將第二列減去第一列
的四倍成為新的第二列) 換成
按照規定的基本列運算 (即第一列不改變, 並將第二列減去第一列
的四倍成為新的第二列) 換成
![]()
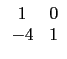
![]() 即為所求.
即為所求.