

下一頁: 四、非選擇題
上一頁: 三、選填題
前一頁: 三、選填題
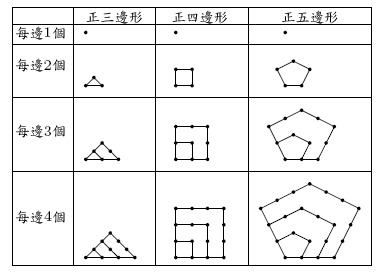
用大小一樣的鋼珠可以排成正三角形、正方形與正五邊形陣列,其排列的規律
如下圖所示:
已知 m 個鋼珠恰好可以排成每邊 n
個鋼珠的正三角形陣列與正方形陣列各一個; 且知若用這 m
個鋼珠去排成每邊 n 個鋼珠的正五邊形陣列時,就會多出 9 個鋼珠。則
n = ?, m = ?
說明:本題是有關於數列與級數的問題. 由於題目的圖示給了很大的提示作用,
同學們應可很容易看出各數列間的關係.
為了方便起見我們令每邊 n 個鋼珠的正三邊形陣列其鋼珠總數為 Tn,
而每邊 n 個鋼珠的正四邊形及正五邊形鋼珠總數分別為 Rn 及 Pn
個. 依題目列出的圖示, 我們有
T1 = 1, T2 = 3, T3 = 6, T4 = 10, 可約略看出
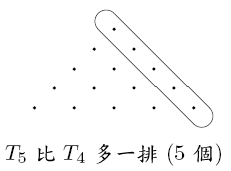
Tn - Tn - 1 = n. 事實上, 每邊 n 個鋼珠的正三邊形是由每邊 n - 1
個鋼珠的正三邊形多加(一排) n 個鋼珠得到的, 如下圖.
依照
Tn = Tn - 1 + n,
Tn - 1 = Tn - 2 + n - 1, 我們可得
Tn = Tn - 2 + n - 1 + n. 如此歸納可得
Tn = 1 + 2 + ... + n = n(n + 1)/2 (亦即
Tn 是以 T1 = 1 為首項公差為 1 的等差級數). 同理, 每邊 n
個鋼珠的正四邊形是由每邊 n - 1 個鋼珠的正四邊形多加兩排得到.
由於這兩排每邊有 n 個鋼珠但有一個接點, 故多出 2n - 1 個鋼珠.
我們得
Rn = Rn - 1 + 2n - 1, 因此由歸納可得
Rn = 1 + 3 + ... + 2n - 1 = n(2n)/2 = n2 (亦即 Rn 是以 R1 = 1
為首項公差為 2 的等差級數). 而每邊 n 個鋼珠的正五邊形是由每邊
n - 1 個鋼珠的正五邊形多加三排得到. 由於這三排每邊有 n
個鋼珠但有兩個接點, 故多出 3n - 2 個鋼珠. 我們得
Pn = Pn - 1 + 3n - 2,
因此由歸納可得
Pn = 1 + 4 + ... + 3n - 2 = n(3n - 1)/2 (亦即 Pn 是以
P1 = 1 為首項公差為 3 的等差級數). 現由題意知 Tn + Rn = m 且
m = Pn + 9, 所以我們有
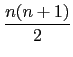
+
n2 =
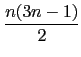
+ 9,
化簡得 n = 9, 再代回得
m = T9 + R9 = 45 + 81 = 126.
其實若等差級數的概念清楚, 我們很快的可以知道 n 等於 9. 因為
Tn, Rn, Pn 皆為等差級數, 所以
Tn + Rn - Pn 亦為等差級數. 又因
Tn, Rn 和 Pn 的公差分別為 1, 2 和 3, 我們知
Tn + Rn - Pn
為一公差為 1 + 2 - 3 = 0 的等差級數. 而此級數之首項為
T1 + R1 - P1 = 1,
故知
Tn +
Rn -
Pn =
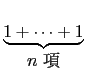
=
n.
因此由題意正三邊形和正四邊形之鋼珠總數多出正五邊形鋼珠九個知 n = 9.


下一頁: 四、非選擇題
上一頁: 三、選填題
前一頁: 三、選填題
Li
2008-08-16

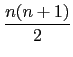 + n2 =
+ n2 = 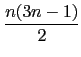 + 9,
+ 9,
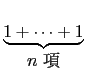 = n.
= n.