

下一頁: 二、多選題
上一頁: 一、單選題
前一頁: 一、單選題
在與水平面成 10o 的東西向山坡上,鉛直(
即與水平面垂直)立起一根旗竿。 當陽光從正西方以俯角 60o
平行投射在山坡上時,旗竿的影子長為 11 公尺,如下圖所示(
其中箭頭表示陽光投射的方向,而粗黑線段表示旗竿的影子)。
試問旗竿的長度最接近以下哪一選項?
(1) 19.1 公尺 (2) 19.8 公尺 (3) 20.7 公尺 (4)
21.1 公尺 (5) 21.7 公尺
參考數值:
sin 10o 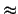 0.174,
sin 20o
0.174,
sin 20o 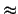 0.342,
cos 10o
0.342,
cos 10o 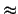 0.985,
cos 20o
0.985,
cos 20o 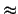 0.940,
0.940,
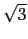
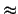 1.732
1.732
說明:本題是一個基本的三角問題, 只要知道要探討哪一個三角形,
運用適當的三角性質(如正弦定理)就能處理.
為方便起見我們令旗杆底為 A, 旗竿影子的頂點設為 B, 而旗杆頂點設為
C. 由於題目已知旗竿的影子長, 而問旗竿的長度,
很自然的我們就是要探討
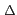 ABC.
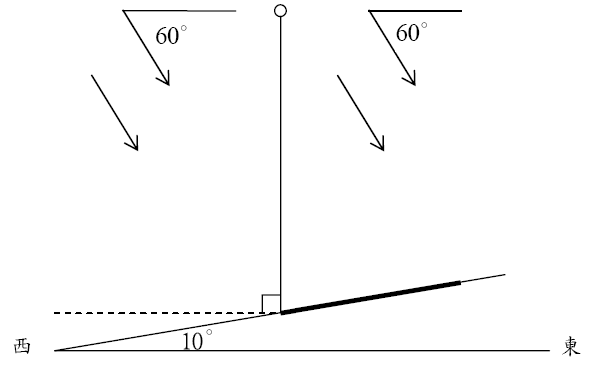
我們沿用一般習慣的符號設定, 直接用 A, B, C 表示三角形 ABC
三個內角的角度, 而分別用 a, b, c 表式角 A, B, C 的對邊 (即
ABC.
我們沿用一般習慣的符號設定, 直接用 A, B, C 表示三角形 ABC
三個內角的角度, 而分別用 a, b, c 表式角 A, B, C 的對邊 (即
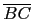 ,
,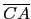 ,
,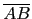 ) 的邊長, 如下圖所示.
) 的邊長, 如下圖所示.
接下來我們將
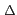 ABC 所知的訊息列出,
由題意知 c = 11, 而
A = 90o - 10o = 80o 且
C = 90o - 60o = 30o, 依此我們可得
B = 180o - (A + C) = 70o. 題目就是要我們依這些訊息求出 b 值.
這可用很多方法處理, 這裡我們想利用由邊角關係確認一個三角形的看法處理
(對此不熟悉的同學, 建議參考``97 學年指考數學乙''選填題 C 的解說).
這是一個 ASA (或 AAS) 的問題, 即知道三角形的三個角和某一邊長.
故利用正弦定理 (
a/sin A = b/sin B = c/sin C) 較合適. 由正弦定理可得
ABC 所知的訊息列出,
由題意知 c = 11, 而
A = 90o - 10o = 80o 且
C = 90o - 60o = 30o, 依此我們可得
B = 180o - (A + C) = 70o. 題目就是要我們依這些訊息求出 b 值.
這可用很多方法處理, 這裡我們想利用由邊角關係確認一個三角形的看法處理
(對此不熟悉的同學, 建議參考``97 學年指考數學乙''選填題 C 的解說).
這是一個 ASA (或 AAS) 的問題, 即知道三角形的三個角和某一邊長.
故利用正弦定理 (
a/sin A = b/sin B = c/sin C) 較合適. 由正弦定理可得
b =
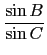
×
c =

×11 = cos 20
o×22
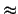
20.68.
Li
2008-08-16

![]() 0.174,
sin 20o
0.174,
sin 20o ![]() 0.342,
cos 10o
0.342,
cos 10o ![]() 0.985,
cos 20o
0.985,
cos 20o ![]() 0.940,
0.940,
![]()
![]() 1.732
1.732
![]() ABC.
我們沿用一般習慣的符號設定, 直接用 A, B, C 表示三角形 ABC
三個內角的角度, 而分別用 a, b, c 表式角 A, B, C 的對邊 (即
ABC.
我們沿用一般習慣的符號設定, 直接用 A, B, C 表示三角形 ABC
三個內角的角度, 而分別用 a, b, c 表式角 A, B, C 的對邊 (即
![]() ,
,![]() ,
,![]() ) 的邊長, 如下圖所示.
) 的邊長, 如下圖所示.
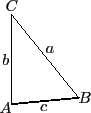
 ×11 = cos 20o×22
×11 = cos 20o×22