Example for designs in 18 runs with
6 three-level
factors using R programs
zipped program [QB.zip]
zipped data files for the programs [R18.out]
noRun=18
noF=6
Input your prior knowledge on
π1 : the
experimenter's prior belief that the linear term xi
is in the true model
(p1).
π2: the
prior
probability that a quadratic effect is in the true model given that
the
linear effect of the same factor is in the model (p2).
π3:
the
prior probability that an interaction is in the true model given
that the
linear effects of both the factors involved are in the model (p3).
Calculate the probability of a model being the best model.
Plot the historgram from prmat
with p1=1, p2=1, p3=0.3
pp=c(1,1,0.5)
prmat=pr.mat(pp,
noF, noRun)
plot.hist(prmat,
noF, noRun)
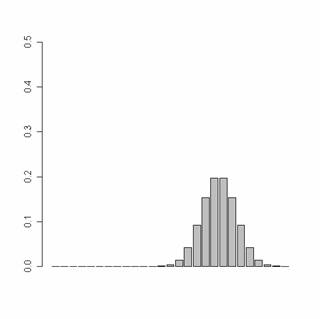
Re-allocate the probabilities of a model being the best model
from
non-eligible models among all models of maximal size.
Here we use adj=r/m, where r is the sum of the prior
probabilities for all non-eligible
models, and m is the number of models with exactly N
parameters.
pr.adj.c=pr.adj(prmat, noRun)
pradj=pr.adj.c$pradj
adj=pr.adj.c$adj
print(adj)
[1] 1.218975e-06
Calculate the
probability of a
model being the best model.
Plot the historgram from prmat
with p1=0.8, p2=0.7, p3=0.3
pp=c(0.8, 0.7, 0.3)
prmat=pr.mat(pp,
noF, noRun)
plot.hist(prmat,
noF, noRun)
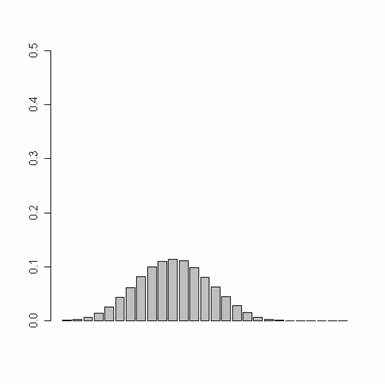
pr.adj.c=pr.adj(prmat, noRun)
pradj=pr.adj.c$pradj
adj=pr.adj.c$adj
print(adj)
[1]
3.468405e-08
> source("Qb18.r")
noF= 4
p1= .8
p2= .7
p3= .6
[1] 0 adj=r/m, where r is the sum of the prior
probabilities for all non-eligible
models, and m is the number of models with exactly N
parameters.
[,1] [,2] [,3] [,4]
del 0 0 0 1337
del 1 0 0 1242
del 1 1 0
621
del 2 0 0 1160
del 2 1 0
580
del 2 0 1
580
del 2 1 1
290
del 2 2 0
290
del 3 0 1
544
del 3 1 1
272
del 3 0 2
272
del 4 0 2
256
[,1] [,2] [,3] [,4]
xi 0 0 0 1.000000
xi 1 0 0 0.800000
xi 1 1 0 0.560000
xi 2 0 0 0.640000
xi 2 1 0 0.448000
xi 2 0 1 0.384000
xi 2 1 1 0.268800
xi 2 2 0 0.313600
xi 3 0 1 0.307200
xi 3 1 1 0.215040
xi 3 0 2 0.184320
xi 4 0 2 0.147456
Read 9288 items
number of isomorphic designs : 129
study design= 1
[,1] [,2] [,3] [,4]
[1,] 1 1
1 1
[2,] 1 1
3 2
[3,] 1 2
1 3
[4,] 1 2
2 2
[5,] 1 3
2 1
[6,] 1 3
3 3
[7,] 2 1
2 1
[8,] 2 1
2 3
[9,] 2 2
3 1
[10,] 2 2
3 3
[11,] 2 3
1 2
[12,] 2 3
1 2
[13,] 3 1
1 3
[14,] 3 1
3 2
[15,] 3 2
1 1
[16,] 3 2
2 2
[17,] 3 3
2 3
[18,] 3 3
3 1
GMA-aberration
A 1 : 0
A 2 : 0
A 3 : 3.3333
A 4 : 0.6667
beta-aberration
B 1 : 0
B 2 : 0
B 3 : 0.0833
B 4 : 0.875
B 5 : 2.1667
B 6 : 0.875
B 7 : 0
B 8 : 0
Q second-order : 0.30208
QB second-order : 0.375
study design= 2
[,1] [,2] [,3] [,4]
[1,] 1 1
1 1
[2,] 1 1
2 2
[3,] 1 2
1 2
[4,] 1 2
3 3
[5,] 1 3
2 3
[6,] 1 3
3 1
[7,] 2 1
2 3
[8,] 2 1
3 1
[9,] 2 2
1 3
[10,] 2 2
3 2
[11,] 2 3
1 1
[12,] 2 3
2 2
[13,] 3 1
1 2
[14,] 3 1
3 3
[15,] 3 2
2 1
[16,] 3 2
2 1
[17,] 3 3
1 3
[18,] 3 3
3 2
GMA-aberration
A 1 : 0
A 2 : 0
A 3 : 2.6667
A 4 : 1.3333
beta-aberration
B 1 : 0
B 2 : 0
B 3 : 0.1042
B 4 : 0.9375
B 5 : 2.0208
B 6 : 0.5625
B 7 : 0.375
B 8 : 0
Q second-order : 0.33854
QB second-order : 0.41667
> source("Qb18.r")
noF= 6
p1= 1
p2= 1
p3= .5
[1] 1.218975e-06 adj
[,1] [,2] [,3] [,4]
del 0 0 0 1613947
del 1 0 0 1575449
del 1 1 0
703517
del 2 0 0 1538288
del 2 1 0
684982
del 2 0 1
684982
del 2 1 1
296146
del 2 2 0
296146
del 3 0 1
667068
del 3 1 1
287228
del 3 0 2
287228
del 4 0 2
278600
[,1] [,2] [,3] [,4]
xi 0 0 0 0.5841588
xi 1 0 0 0.5836041
xi 1 1 0 0.3783104
xi 2 0 0 0.5830495
xi 2 1 0 0.3778667
xi 2 0 1 0.2718792
xi 2 1 1 0.1588924
xi 2 2 0 0.2648799
xi 3 0 1 0.2714355
xi 3 1 1 0.1585437
xi 3 0 2 0.1251880
xi 4 0 2 0.1248394
Read 47520 items
number of isomorphic designs : 440
study design= 1
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 1
1 1 1 2
[2,] 1 1
2 3 3 1
[3,] 1 2
1 2 2 1
[4,] 1 2
3 1 3 3
[5,] 1 3
2 2 1 3
[6,] 1 3
3 3 2 2
[7,] 2 1
3 1 2 1
[8,] 2 1
3 2 1 3
[9,] 2 2
1 3 3 3
[10,] 2 2
2 2 2 2
[11,] 2 3
1 3 1 1
[12,] 2 3
2 1 3 2
[13,] 3 1
1 2 3 2
[14,] 3 1
2 3 2 3
[15,] 3 2
2 1 1 1
[16,] 3 2
3 3 1 2
[17,] 3 3
1 1 2 3
[18,] 3 3
3 2 3 1
GMA-aberration
A 1 : 0
A 2 : 0
A 3 : 12
A 4 : 16.5
A 5 : 6
A 6 : 5
beta-aberration
B 1 : 0
B 2 : 0
B 3 : 1.1875
B 4 : 5.0781
B 5 : 10.7656
B 6 : 8.1406
B 7 : 5
B 8 : 5.3594
B 9 : 1.8906
B 10 : 1.5469
B 11 : 0.2813
B 12 : 0.25
Q second-order : 2.461
QB second-order : 2.7343
study design= 2
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 1
1 1 2 1
[2,] 1 1
2 3 1 2
[3,] 1 2
1 2 1 3
[4,] 1 2
3 1 3 2
[5,] 1 3
2 2 3 1
[6,] 1 3
3 3 2 3
[7,] 2 1
2 2 3 3
[8,] 2 1
3 1 1 3
[9,] 2 2
1 3 3 2
[10,] 2 2
3 2 2 1
[11,] 2 3
1 3 1 1
[12,] 2 3
2 1 2 2
[13,] 3 1
1 2 2 2
[14,] 3 1
3 3 3 1
[15,] 3 2
2 1 1 1
[16,] 3 2
2 3 2 3
[17,] 3 3
1 1 3 3
[18,] 3 3
3 2 1 2
GMA-aberration
A 1 : 0
A 2 : 0
A 3 : 11.3333
A 4 : 18.5
A 5 : 4
A 6 : 5.6667
beta-aberration
B 1 : 0
B 2 : 0
B 3 : 0.9583
B 4 : 5.5312
B 5 : 11
B 6 : 6.9531
B 7 : 5.9687
B 8 : 5.3906
B 9 : 1.4792
B 10 : 1.3594
B 11 : 0.8438
B 12 : 0.0156
Q second-order : 2.43373
QB second-order : 2.72531
study design= 3
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 1
1 1 1 2
[2,] 1 1
2 3 2 1
[3,] 1 2
1 2 3 1
[4,] 1 2
3 1 2 3
[5,] 1 3
2 2 1 3
[6,] 1 3
3 3 3 2
[7,] 2 1
2 2 2 2
[8,] 2 1
3 1 3 1
[9,] 2 2
1 3 2 3
[10,] 2 2
3 2 1 2
[11,] 2 3
1 3 1 1
[12,] 2 3
2 1 3 3
[13,] 3 1
1 2 3 3
[14,] 3 1
3 3 1 3
[15,] 3 2
2 1 1 1
[16,] 3 2
2 3 3 2
[17,] 3 3
1 1 2 2
[18,] 3 3
3 2 2 1
GMA-aberration
A 1 : 0
A 2 : 0
A 3 : 12
A 4 : 16.5
A 5 : 6
A 6 : 5
beta-aberration
B 1 : 0
B 2 : 0
B 3 : 1.1875
B 4 : 5.125
B 5 : 10.8359
B 6 : 7.918
B 7 : 5.3047
B 8 : 4.7617
B 9 : 2.2891
B 10 : 1.4414
B 11 : 0.6328
B 12 : 0.0039
Q second-order : 2.48058
QB second-order : 2.75586
study design= 5
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 1
1 1 2 2
[2,] 1 1
2 2 1 1
[3,] 1 2
1 3 3 3
[4,] 1 2
3 3 1 2
[5,] 1 3
2 1 3 1
[6,] 1 3
3 2 2 3
[7,] 2 1
3 1 3 3
[8,] 2 1
3 3 2 1
[9,] 2 2
1 1 1 1
[10,] 2 2
2 2 2 2
[11,] 2 3
1 2 3 2
[12,] 2 3
2 3 1 3
[13,] 3 1
1 2 1 3
[14,] 3 1
2 3 3 2
[15,] 3 2
2 1 2 3
[16,] 3 2
3 2 3 1
[17,] 3 3
1 3 2 1
[18,] 3 3
3 1 1 2
GMA-aberration
A 1 : 0
A 2 : 0
A 3 : 11.3333
A 4 : 18.5
A 5 : 4
A 6 : 5.6667
beta-aberration
B 1 : 0
B 2 : 0
B 3 : 1.5208
B 4 : 4.0781
B 5 : 10.7656
B 6 : 10.1406
B 7 : 4
B 8 : 4.3594
B 9 : 2.5573
B 10 : 1.5469
B 11 : 0.2813
B 12 : 0.25
Q second-order : 2.57904
QB second-order : 2.79607
study design=0 (to stop)