Nonlinear Energy Minimization for
Surface Parameterizations
Surface Parameterizations
Mei-Heng Yueh
Department of Mathematics
National Taiwan Normal University
Outline
Introduction
Overview of State-of-the-Arts
Conformal and Authalic Parameterizations
Applications in Computer Graphics
Volume-Preserving Parameterizations
Application to Brain Tumor Segmentation
Introduction
Simplicial Surfaces
A simplicial surface is a piecewise linear manifold composed of simplices.

|

|
| simplicial surface | simplicial 3-manifold |
| composed of triangles | composed of tetrahedrons |
Parameterization Problem
The parameterization problem aims to find a bijective map $f$ that maps
| a given simplicial manifold | to | a domain of a specified shape |

|
$\xrightarrow{~~~~~f~~~~~}$ |

|
| $\mathcal{M}$ | $\mathcal{D}$ |
while minimizing a specified distortion.
Coordinate Charts Induced by Parameterizations
Surface Parameterizations
A coordinate system on the surface is induced by the parameterization.




A desired parameterization usually preserves the local shape well.
Conformal mappings are good options!
Conformal Mappings
Uniformization theorem guarantees the existence of conformal maps.
The computation of conformal mappings has been extensively studied.
Overview of State-of-the-Arts
Disk Conformal Parameterizations
 
|
|
[HuGH14] Huang, Gu, Huang, Lin, Lin and Yau, Geom Imag Comput, 1(2):223–258, 2014.
[ChLu15] Choi and Lui, J Sci Comput, 65(3):1065–1090, 2015.
[YuLW17] Yueh, Lin, Wu and Yau, J Sci Comput, 73(1):203–227, 2017.
[ChLu18] Choi and Lui, Adv Comput Math, 44:87–114, 2018.
[KuLY21] Kuo, Lin, Yueh and Yau, SIAM J Imaging Sci, 14(4):1790–1815, 2021.
[LiYu22] Liao and Yueh, J Sci Comput, 92(2), 2022.
Free-Boundary Conformal Parameterizations
 
|
|
[ShSt01] Sheffer and Sturler, Eng with Comput, 17(3):326–337, 2001.
[LePR02] Lévy, Petitjean, Ray and Maillot, ACM Trans Graph, 21(3):362–371, 2002.
[ShLM05] Sheffer, Lévy, Mogilnitsky and Bogomyakov, ACM Trans Graph, 24(2):311–330, 2005.
[MuTA08] Mullen, Tong, Alliez and Desbrun, SGP ’08, 27(5):1487–1494, 2008.
[HuGL14] Huang, Gu, Lin and Yau, J Sci Comput, 61(3):558–583, 2014.
[SaCr17] Sawhney and Crane, ACM Trans Graph, 37(1):5:1–5:14, 2017.
Spherical Conformal Parameterizations
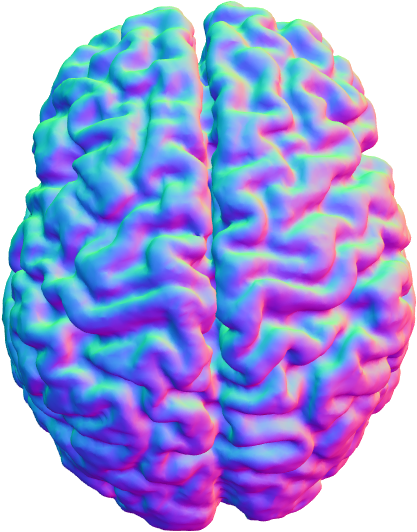 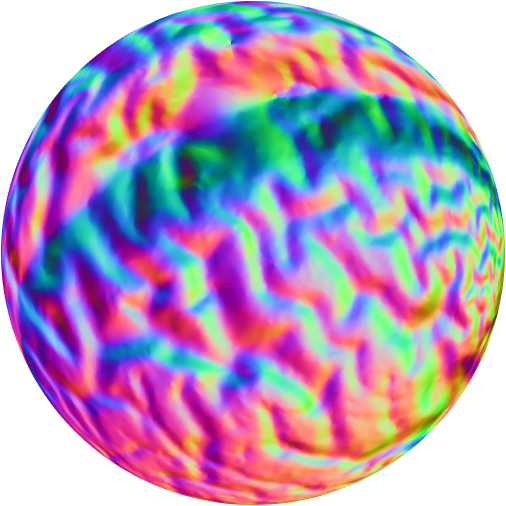
|
|
[AnHT99] Angenent, Haker, Tannenbaum and Kikinis, IEEE Trans Med Imaging, 18(8):700–711, 1999.
[GuWC04] Gu, Wang, Chan, Thompson and Yau, IEEE Trans Med Imaging, 23(8):949–958, 2004.
[HuGH14] Huang, Gu, Huang, Lin, Lin and Yau, Geom Imag Comput, 1(2):223–258, 2014.
[ChLL15] Choi, Lam and Lui, SIAM J Imaging Sci, 8(1):67–94, 2015.
[YuLL19] Yueh, Li, Lin and Yau, SIAM J Imaging Sci, 12(2):1071–1098, 2019.
Authalic (Area-Preserving) Parameterizations
 
|
|
[YoBS04] Yoshizawa, Belyaev and Seidel, Proceedings Shape Modeling Applications, 200-208, 2004.
[ZoHG11] Zou, Hu, Gu and Hua, IEEE T Vis Comput Gr, 17(12):2005-2014, 2011.
[ZhSG13] Zhao, Su, Gu, Kaufman, Sun, Gao and Luo, IEEE T Vis Comput Gr, 19(12):2838-2847, 2013.
[YuLW19] Yueh, Lin, Wu and Yau, J Sci Comput, 78(3): 1353–1386, 2019.
Volume-Preserving Parameterizations
|
|
[JiQZ15] Jin, Qian, Zhao, Chang, Tong and Zhang, J Comput Sci Technol, 30:553–564, 2015.
[SuCL17] Su, Chen, Lei, Zhang, Qian and Gu, Comput Aided Design, 82:42-56, 2017.
[YuLL19] Yueh, Li, Lin and Yau, SIAM J Imaging Sci, 12(2):1071–1098, 2019.
[YuLL20] Yueh, Li, Lin and Yau, SIAM J Imaging Sci, 13(3):1536–1564, 2020.
Energy Minimization-Based Methods
Energy Minimization-Based Methods



Minimize nonlinear energy functionals of the form $$ E(f) = \frac{1}{2}\mathbf{v}(f)^\top L(f) \, \mathbf{v}(f) $$ subject to a boundary shape constraint $f(\partial\mathcal{M}) = \partial\mathcal{D}$, where $\mathbf{v}(f)$ and $L(f)$ are vector and matrix dependent on $f$, respectively.
Main Targets
 |
 |
 |
 |
 |
| Surface | Disk Conformal | Disk Area-Preserving | Square Conformal | Square Area-Preserving |
- Prove the minimizer is the desired parameterization.
- Develop efficient algorithm for the energy minimization.
- Prove the convergence of the proposed algorithms.
Simplicial Surfaces and Maps
Simplicial Surface

|
A simplicial surface $\mathcal{M}$ is composed of \begin{align*} \text{vertices } \mathcal{V}(\mathcal{M}) &= \left\{ {v}_1, \ldots, {v}_n \right\} \subset \mathbb{R}^3,\\ \text{edges } \mathcal{E}(\mathcal{M}) &= \left\{ [ {v}_i, {v}_j ] \right\},\\ \text{faces } \mathcal{F}(\mathcal{M}) &= \left\{ [ {v}_i, {v}_j, {v}_k ] \right\}, \end{align*} $$ [ {v}_1, \ldots, v_d ] := \left\{ \sum_{k=1}^d \alpha_k v_k \,\left|\, \alpha_k>0, \,\sum_{k=1}^d \alpha_k = 1 \right.\right\}. $$ |
Simplicial Map
A simplicial map $f$ is a piecewise affine map with $f(v_k)=\mathbf{f}_k\in\mathbb{R}^2$.
 $\xrightarrow{~~~~~f:\mathcal{M}\to\mathbb{R}^2~~~~~}$
$\xrightarrow{~~~~~f:\mathcal{M}\to\mathbb{R}^2~~~~~}$

The map $f$ is represented as a matrix $$ \mathbf{f} = \begin{bmatrix} f(v_1) \\ \vdots \\ f(v_n) \end{bmatrix} = \begin{bmatrix} \mathbf{f}_1^\top \\ \vdots \\ \mathbf{f}_n^\top \end{bmatrix} = \begin{bmatrix} \mathbf{f}^1_1 & \mathbf{f}^2_1 \\ \vdots & \vdots \\ \mathbf{f}^1_n & \mathbf{f}^2_n \end{bmatrix} = \begin{bmatrix} \mathbf{f}^1 & \mathbf{f}^2 \end{bmatrix}\in\mathbb{R}^{n\times 2}, $$ or a vector $({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top)^\top \in\mathbb{R}^{2n}$.
Simplicial Map
|
On the triangle $\sigma = [{v}_i, {v}_j, {v}_k]$, \begin{align} f|_{\sigma}({\color{yellow}v}) &= \frac{|[{\color{yellow}v}, {v}_j, {v}_k]|}{|\sigma|} \,{f}(v_i)\\ &+ \frac{|[{v}_i, {\color{yellow}v}, {v}_k]|}{|\sigma|} \,{f}(v_j) \\ &+ \frac{|[{v}_i, {v}_j, {\color{yellow}v}]|}{|\sigma|} \,{f}(v_k), \end{align} $|\sigma|$ denotes the area of $\sigma$. |
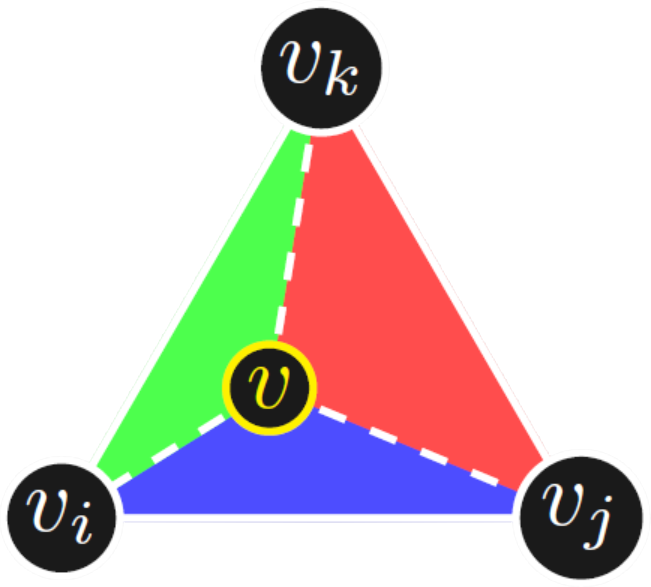 Barycentric coordinates of ${\color{yellow}v}$: $\left(\frac{|[{\color{yellow}v}, {v}_j, {v}_k]|}{|\sigma|}, \frac{|[{v}_i, {\color{yellow}v}, {v}_k]|}{|\sigma|}, \frac{|[{v}_i, {v}_j, {\color{yellow}v}]|}{|\sigma|}\right)$ |
Simplicial 3-Complex

|
A simplicial $3$-complex $\mathcal{M}$ is composed of \begin{align*} \text{vertices } \mathcal{V}(\mathcal{M}) &= \left\{ {v}_1, \ldots, {v}_n \right\} \subset \mathbb{R}^3,\\ \text{edges } \mathcal{E}(\mathcal{M}) &= \left\{ [ {v}_i, {v}_j ] \right\},\\ \text{faces } \mathcal{F}(\mathcal{M}) &= \left\{ [ {v}_i, {v}_j, {v}_k ] \right\},\\ \text{tetrahedrons } \mathcal{T}(\mathcal{M}) &= \left\{ [ {v}_i, {v}_j, {v}_k, {v}_\ell ] \right\}, \end{align*} where $$ [ {v}_1, \ldots, v_d ] := \left\{ \sum_{k=1}^d \alpha_k v_k \,\left|\, \alpha_k>0, \,\sum_{k=1}^d \alpha_k = 1 \right.\right\}. $$ |
Simplicial Map
A simplicial map $f$ is a piecewise affine map with $f(v_k)=\mathbf{f}_k\in\mathbb{R}^3$.
 $\xrightarrow{~~~~~f:\mathcal{M}\to\mathbb{R}^3~~~~~}$
$\xrightarrow{~~~~~f:\mathcal{M}\to\mathbb{R}^3~~~~~}$

The map $f$ is represented as a matrix $$ \mathbf{f} = \begin{bmatrix} f(v_1) \\ \vdots \\ f(v_n) \end{bmatrix} = \begin{bmatrix} \mathbf{f}_1^\top \\ \vdots \\ \mathbf{f}_n^\top \end{bmatrix} = \begin{bmatrix} \mathbf{f}^1_1 & \mathbf{f}^2_1 & \mathbf{f}^3_1 \\ \vdots & \vdots & \vdots \\ \mathbf{f}^1_n & \mathbf{f}^2_n & \mathbf{f}^3_n \end{bmatrix} = \begin{bmatrix} \mathbf{f}^1 & \mathbf{f}^2 & \mathbf{f}^3 \end{bmatrix}\in\mathbb{R}^{n\times 3}, $$ or a vector $({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top, {\mathbf{f}^3}^\top)^\top \in\mathbb{R}^{3n}$.
Conformal Parameterizations
Conformal Energy Minimization (CEM) [KuLY21]
The CEM aims to find a disk conformal map.
 $\xrightarrow{~~~~~f~~~~~}$
$\xrightarrow{~~~~~f~~~~~}$

[KuLY21] Kuo, Lin, Yueh and Yau, SIAM J Imaging Sci, 14(4):1790–1815, 2021.
Conformal Energy Functional
The conformal energy of a smooth map $f$ is defined as \[ \mathcal{E}_C(f) = \mathcal{E}_D(f) - \mathcal{A}(f), \] where $\mathcal{E}_D$ is the Dirichlet energy defined as \[ \mathcal{E}_D\left({f}\right) = \frac{1}{2}\int_\mathcal{M} \|\nabla {f}\|^2 \,\mathrm{d} \sigma_\mathcal{M}. \]
Lower Bound of Dirichlet Energy
| Theorem [Hutc91] |
The Dirichlet energy satisfies $\mathcal{E}_D(f) \geq \mathcal{A}(f).$ The equality holds if and only if $f$ is conformal. |
\begin{align*} \mathcal{E}_D\left({f}\right) &= \frac{1}{2}\int_\mathcal{M} \|\nabla {f}\|^2 \,\mathrm{d} \sigma_\mathcal{M} = \frac{1}{2}\int_\mathcal{M} ( \|{f}_u\|^2 + \|{f}_v\|^2 ) \,\mathrm{d} u \,\mathrm{d} v\\ &\geq \int_\mathcal{M} \|{f}_u\| \|{f}_v\| \,\mathrm{d} u \,\mathrm{d} v \geq \int_\mathcal{M} \|{f}_u \times {f}_v\| \,\mathrm{d} u \,\mathrm{d} v = \mathcal{A}(f). \end{align*} The equality holds if and only if $ \|{f}_u\| = \|{f}_v\| ~\text{ and }~ {f}_u \perp {f}_v. $
| Corollary [Hutc91] | $\mathcal{E}_C(f) \equiv \mathcal{E}_D(f) - \mathcal{A}(f) = 0$ $\iff$ $f$ is conformal. |
Discrete Dirichlet Energy
The discrete Dirichlet energy functional \begin{align*} {E}_D(f) &\equiv \frac{1}{2}\sum_{\tau\in\mathcal{F}(\mathcal{M})} \left\|(\nabla f)|_\tau \right\|^2 |\tau| \\ &= \frac{1}{2}\sum_{\tau\in\mathcal{F}(\mathcal{M})} \sum_{i\neq j}\frac{\cot\theta_{i,j}}{2}\|f(v_j)-f(v_i)\|^2. \end{align*}
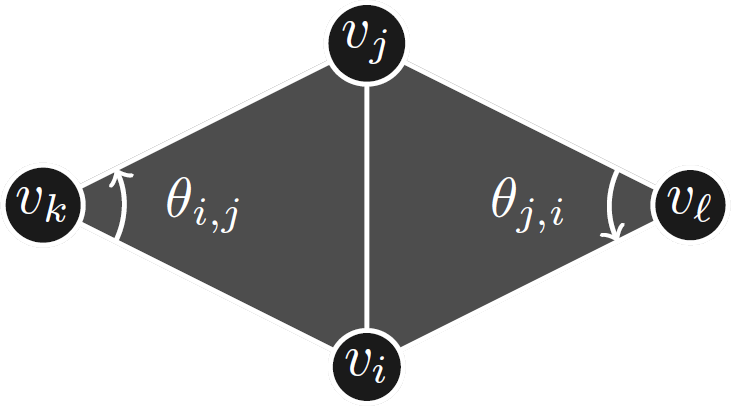
Discrete Dirichlet Energy
The discrete Dirichlet energy can be represented as \[ {E}_{D}(f) = \frac{1}{2} \, \mathrm{trace}\left(\mathbf{f}^{\top} {L}_D \mathbf{f}\right) = \frac{1}{2} \,({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top) \begin{bmatrix} {L}_D \\ & {L}_D \end{bmatrix} \begin{bmatrix} \mathbf{f}^1\\ \mathbf{f}^2 \end{bmatrix}, \] where $L_D$ is the discrete Laplace–Beltrami operator with $$ [{L}_D]_{i,j} = \begin{cases} -\frac{1}{2}\left(\cot\theta_{i,j}+\cot\theta_{j,i}\right) &\mbox{if $[{v}_i,{v}_j]\not\subset\partial\mathcal{M}$,}\\ -\frac{1}{2}\cot\theta_{i,j} &\mbox{if $[{v}_i,{v}_j]\subset\partial\mathcal{M}$,}\\ -\sum_{k\neq i} [{L}_D]_{i,k} &\mbox{if $i = j$,} \\ 0 &\mbox{otherwise.} \end{cases} $$
Image Area
The area of the image $f(\mathcal{M})$ can be written as \begin{equation*}%\label{eqn:Area} \mathcal{A}(f) = \frac{1}{2} \sum_{[{v}_i,{v}_j] \in \partial \mathcal{M}} ({f}^1_{i} {f}^2_{j} - {f}^1_{j} {f}^2_{i}) = \frac{1}{2} \, ({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top) \begin{bmatrix} \mathbf{0} & {S}^{\top}\\ {S} & \mathbf{0} \end{bmatrix} \begin{bmatrix} \mathbf{f}^1\\ \mathbf{f}^2 \end{bmatrix}, \end{equation*} with ${S}^{\top} = -{S}$.
Discrete Conformal Energy \begin{equation*} {E}_{C}({f}) = {E}_{D}({f}) - \mathcal{A}({f}) = \frac{1}{2} \, ({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top) \begin{bmatrix} {L}_D & {S}\\ -{S} & {L}_D \end{bmatrix} \begin{bmatrix} \mathbf{f}^1\\ \mathbf{f}^2 \end{bmatrix}. \end{equation*}
Disk Image Area
Let $n$ be the number of boundary vertices. The area of the polygon with vertices located on $\mathbb{S}^1$ can be represented in polar coordinates as \begin{align*} \mathcal{A}({f}) &=\frac{1}{2} \underbrace{\left[\begin{array}{c}\cos \theta_1\\\cos \theta_2\\\vdots\\\cos \theta_n\end{array}\right]^{\top}}_{\mathbf{c}^{\top}} \underbrace{\left[\begin{array}{cccc}0&1&&-1\\ -1&\ddots&\ddots&\\ &\ddots&\ddots&1\\ 1& & -1&0\end{array}\right]}_{D} \underbrace{\left[\begin{array}{c}\sin \theta_1\\\sin \theta_2\\\vdots\\\sin \theta_n\end{array}\right]}_{\mathbf{s}} \equiv \frac{1}{2}\mathbf{c}^\top D \mathbf{s}. \end{align*}
Discrete Conformal Energy
The discrete conformal energy can be reformulated as \begin{align*} E_C(\boldsymbol{\theta})=\frac{1}{2}\mathbf{c}^{\top}K\mathbf{c} + \frac{1}{2}\mathbf{s}^{\top}K\mathbf{s} - \frac{1}{2}\mathbf{c}^{\top}D\mathbf{s}, \end{align*} where $ K=[{L}_D]_{\mathtt{B},\mathtt{B}}-[{L}_D]_{\mathtt{I},\mathtt{B}}^{\top}[{L}_D]_{\mathtt{I},\mathtt{I}}^{-1}[{L}_D]_{\mathtt{I},\mathtt{B}}\in \mathbb{R}^{n\times n}, $ $$ \mathtt{B} = \{ b \mid v_b \in \partial\mathcal{M} \} ~\text{ and }~ \mathtt{I} = \{ i \mid v_i \in \mathcal{M}\backslash\partial\mathcal{M} \}. $$
Discrete CEM Problem
The discrete CEM problem is formulated as \begin{align*} \min\{E_C(\boldsymbol{\theta})\ |\ 0=\theta_1 < \cdots < \theta_n < 2\pi\}. \end{align*}
| Theorem [KuLY21] | Under some mild conditions, the discrete CEM problem has a nontrivial local minimizer. |
[KuLY21] Kuo, Lin, Yueh and Yau, SIAM J Imaging Sci, 14(4):1790–1815, 2021.
Gradient Descent for CEM
The gradient of $E_C$ can be written as \begin{align*} \nabla E_C(\boldsymbol{\theta}) &= {\rm diag}(\mathbf{c})K\mathbf{s} - {\rm diag}(\mathbf{s})K\mathbf{c} + \frac{1}{2}\left({\rm diag}(\mathbf{c})D\mathbf{c}+{\rm diag}(\mathbf{s})D\mathbf{s}\right). \end{align*} The critical point $\boldsymbol{\theta}$ satisfies $\nabla E_C(\boldsymbol{\theta})=\mathbf{0}$.
| Theorem [KuLY21] | The gradient method for the CEM converges globally. |
[KuLY21] Kuo, Lin, Yueh and Yau, SIAM J Imaging Sci, 14(4):1790–1815, 2021.
Numerical Results
 |
 |
 |
 |
 |
 |
 |
 |
Comparison of Angular Distortions
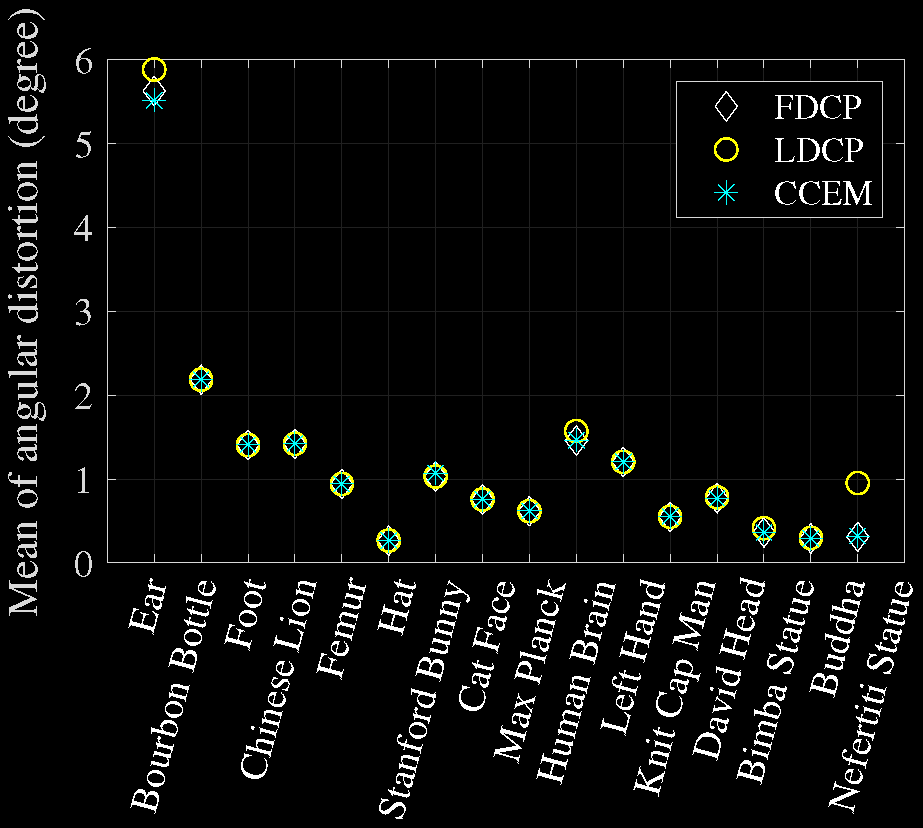
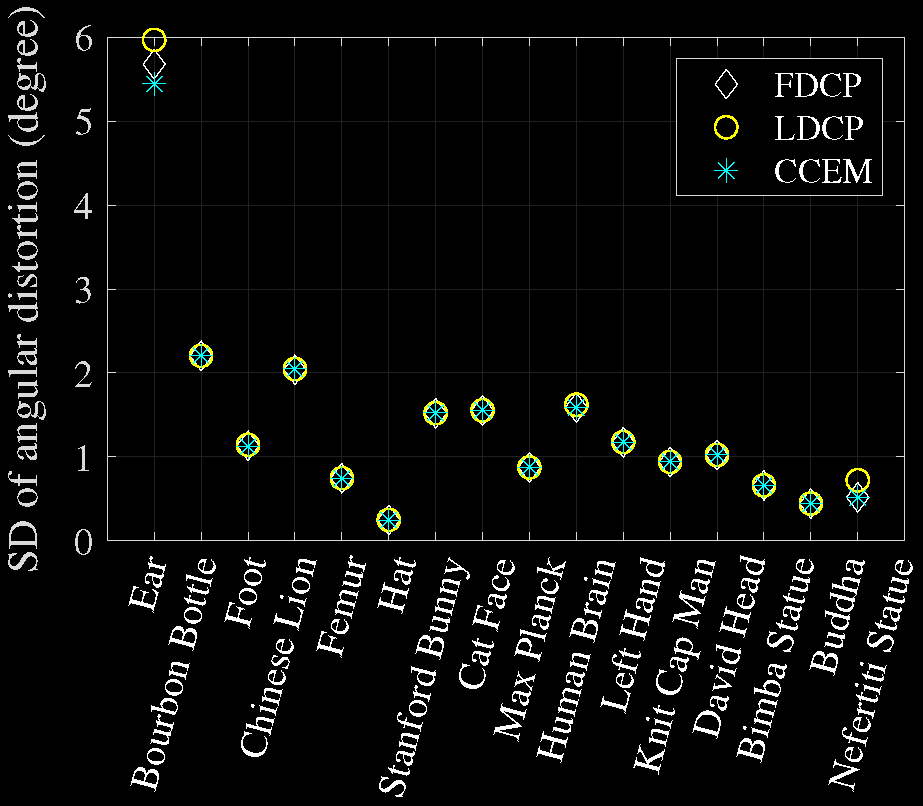
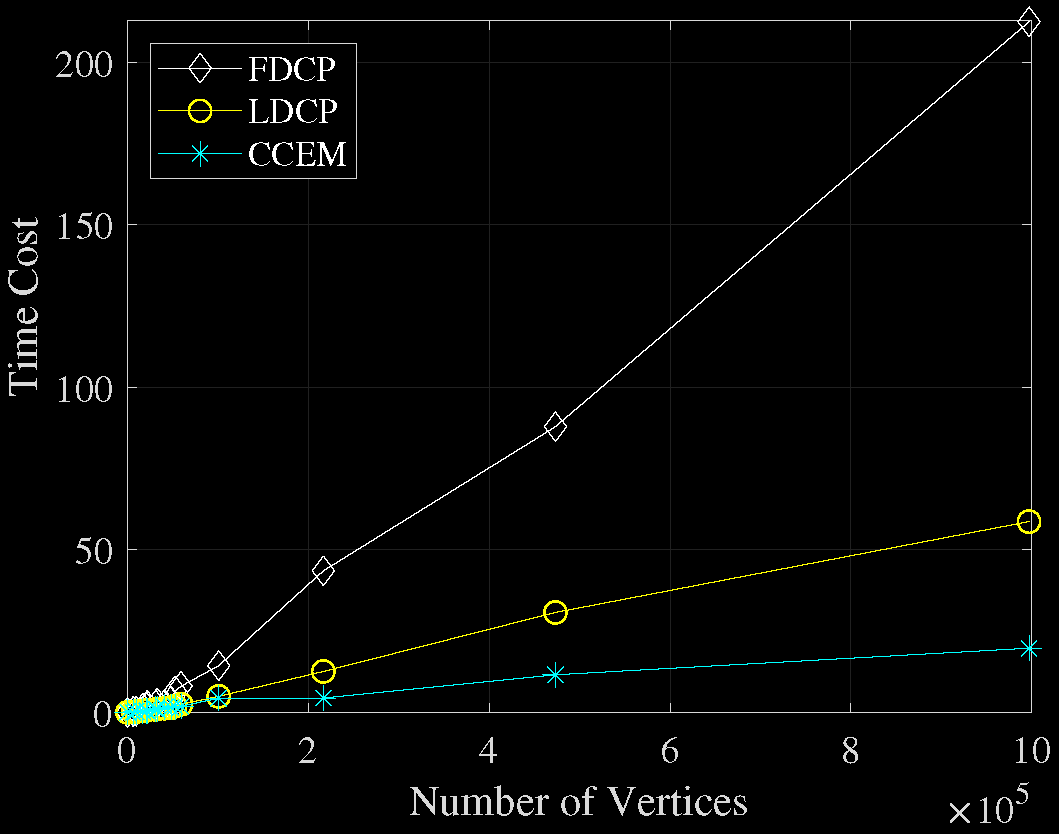
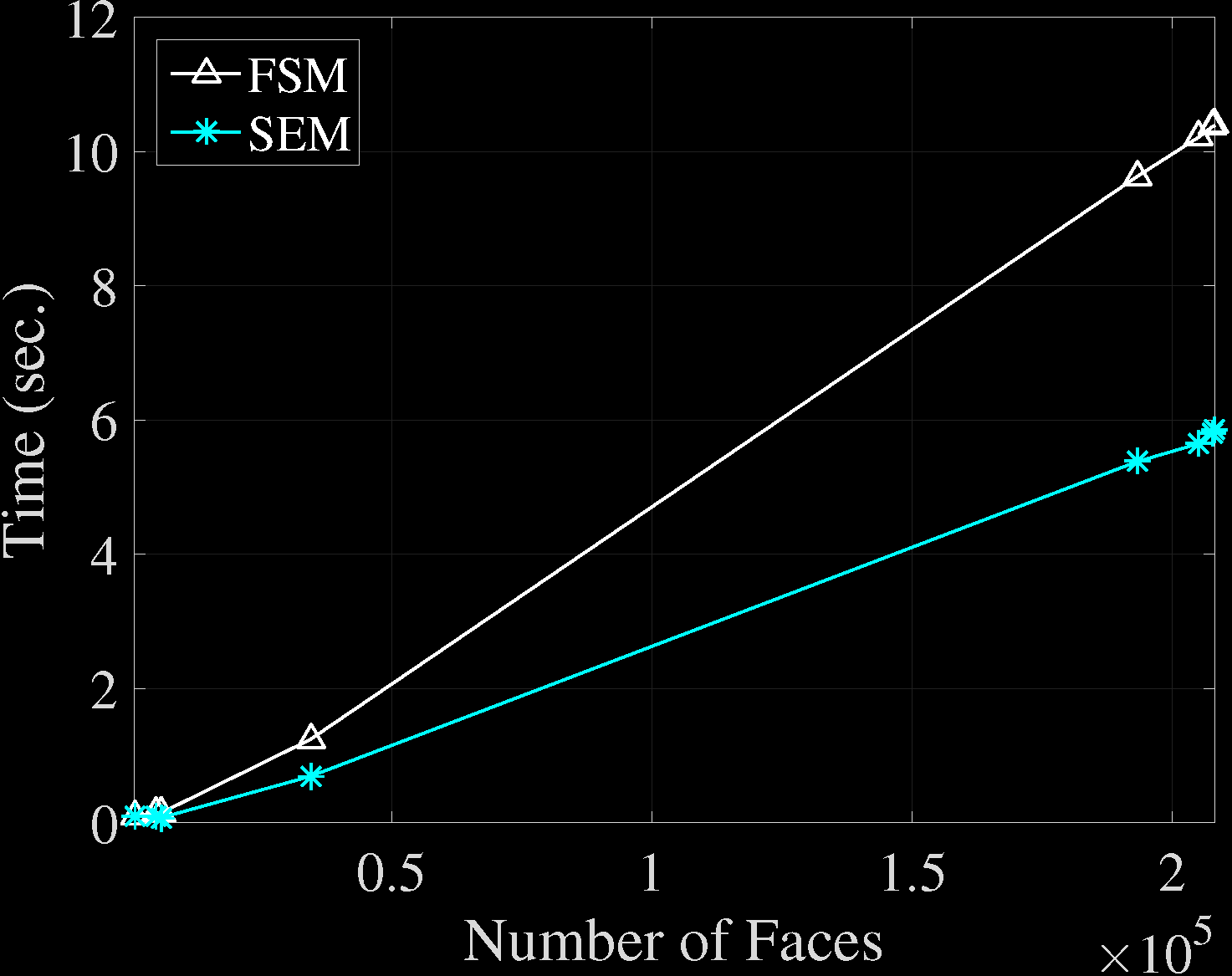
Comparison of Time Costs
Authalic Parameterizations
Stretch Energy Minimization (SEM) [YuLW19]
The SEM aims to find a disk authalic (area-preserving) map.
 $\xrightarrow{~~~~~f~~~~~}$
$\xrightarrow{~~~~~f~~~~~}$

[YuLW19] Yueh, Lin, Wu and Yau, J Sci Comput, 78(3): 1353–1386, 2019.
Stretch Energy Functional [YuLW19]
The stretch energy functional is defined as $$ {E}_S(f) = \frac{1}{2} \text{trace}\left(\mathbf{f}^{\top} {L_S(f)} \, \mathbf{f} \right) = \frac{1}{2} \,({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top) \begin{bmatrix} {L}_S(f) \\ & {L}_S(f) \end{bmatrix} \begin{bmatrix} \mathbf{f}^1\\ \mathbf{f}^2 \end{bmatrix}, $$ where $L_S(f)$ is the stretched Laplacian matrix with $$ [{L}_S(f)]_{i,j} = \begin{cases} -\frac{1}{2}\left(\frac{\cot\theta_{i,j}(f)}{\color{yellow}{\frac{|[v_i,v_j,v_k]|}{|f([v_i,v_j,v_k])|}}}+\frac{\cot\theta_{j,i}(f)}{\color{yellow}{\frac{|[v_j,v_i,v_\ell]|}{|f([v_j,v_i,v_\ell])|}}}\right) &\mbox{if $[{v}_i,{v}_j]\in\mathcal{F}(\mathcal{M})$,}\\ -\sum_{k\neq i} [{L}_S(f)]_{i,k} &\mbox{if $i = j$,} \\ 0 &\mbox{otherwise.} \end{cases} $$
[YuLW19] Yueh, Lin, Wu and Yau, J Sci Comput, 78(3): 1353–1386, 2019.
Lower Bound of Stretch Energy
| Theorem [Yueh22] |
The stretch energy satisfies ${E}_S(f) \geq \mathcal{A}(f).$ The equality holds if and only if $f$ is authalic. |
\begin{align*} E_S(f) &= \frac{1}{2} \sum_{s=1}^2 \sum_{\tau=[v_i,v_j,v_k]\in\mathcal{F}(\mathcal{M})} \begin{bmatrix} f_i^s & f_j^s & f_k^s \end{bmatrix} [L_S(f)]_{\tau} \begin{bmatrix} f_i^s \\ f_j^s \\ f_k^s \end{bmatrix} \\ &= \sum_{\tau\in\mathcal{F}(\mathcal{M})} \frac{|f(\tau)|^2}{|\tau|} \geq \sum_{\tau\in\mathcal{F}(\mathcal{M})} |f(\tau)| = \mathcal{A}(f). \end{align*} The equality holds if and only if $|f(\tau)| = |\tau|$, for every $\tau\in\mathcal{F}(\mathcal{M})$.
| Corollary [Yueh22] | ${E}_A(f) \equiv {E}_S(f) - \mathcal{A}(f) = 0$ $\iff$ $f$ is authalic. |
Gradient Formula of Stretch Energy
| Proposition [Yueh22] | The gradient of $E_S$ can be formulated as \begin{align*} \nabla_{\mathbf{f}^s} E_S(f) &= 2 L_S(f) \, \mathbf{f}^s, ~\text{for $s=1,2$.} \end{align*} |
$$ [\nabla_{\mathbf{f}^s} E_S(f)]_\ell = [L_S(f) \, \mathbf{f}^s]_\ell + \underbrace{\frac{1}{2} \sum_{t=1}^2 \sum_{i=1}^n \sum_{j=1}^n f_i^t f_j^t \frac{\partial}{\partial f_\ell^s}[L_S(f)]_{i,j}}_{(*)}. $$ It suffices to check $(*) = [L_S(f) \, \mathbf{f}^s]_\ell$.
Fixed Point Iteration for SEM
The critical point $f$ satisfies $L_S(f) \, \mathbf{f}^s =\mathbf{0}$, for $s=1,2$. Under a given boundary constraint $\mathbf{f}^s_\mathtt{B} = \mathbf{g}^s$, the critical point $f$ satisfies $$ [L_S(f)]_{\mathtt{I},\mathtt{I}} \mathbf{f}^s_{\mathtt{I}} = -[L_S(f)]_{\mathtt{I},\mathtt{B}} \mathbf{g}^s. $$
Let \begin{equation*} \varphi^s(f) = \begin{bmatrix} -[L_S(f)]_{\mathtt{I},\mathtt{I}}^{-1} [L_S(f)]_{\mathtt{I},\mathtt{B}} \mathbf{g}^s \\ \mathbf{g}^s \end{bmatrix}, ~\text{for $s=1,2$}. \end{equation*}
| Algorithm [YuLW19] | $ {\mathbf{f}^s}^{(n+1)} = \varphi^s(f^{(n)}), ~ \text{for $s=1,2$}. $ |
[YuLW19] Yueh, Lin, Wu and Yau, J Sci Comput, 78(3): 1353–1386, 2019.
Numerical Results
 |
 |
 |
 |
 |
 |
 |
 |
Comparison of Area Distortions
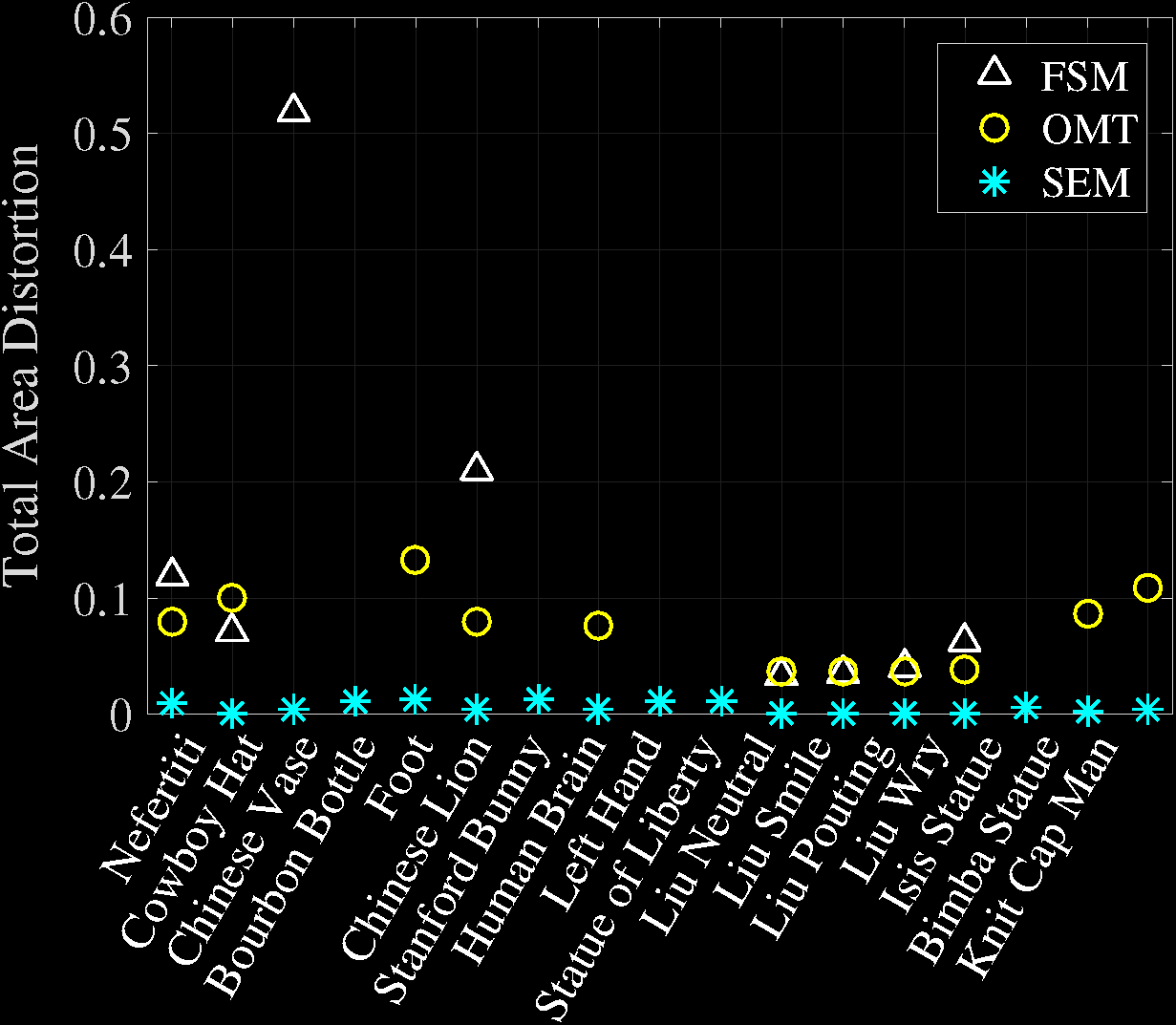
Comparison of Time Costs
Applications in Computer Graphics
Image Editing





|





|
Surface Texture Mapping
Texture mapping aims to map the colors from an image to the surface.

Texture Mapping
The texture is mapped to the surface by a parameterization.

Animation with Texture
The motion can be constructed by the cubic spline homotopy.
Surface Alignment and Fusion [YuHL20]



[YuHL20] Yueh, Huang, Li, Lin and Yau, Elec Trans Num Anal, 53:383–405, 2020.
Fused Model
Volume-Preserving Parameterizations
Volumetric Stretch Energy Minimization (VSEM) [YuLL19]
The VSEM aims to find a spherical volume-preserving map.
 $\xrightarrow{~~~~~f~~~~~}$
$\xrightarrow{~~~~~f~~~~~}$

[YuLL19] Yueh, Li, Lin and Yau, SIAM J Imaging Sci, 12(2):1071–1098, 2019.
Volumetric Stretch Energy Functional [YuLL19]
The volumetric stretch energy functional is defined as
$$
{E}_{\mathbb{S}}({f}) = \frac{1}{2}\mathrm{trace}\left(\mathbf{f}^\top L_{\mathbb{S}}(f) \, \mathbf{f}\right)
= \frac{1}{2} \,({\mathbf{f}^1}^\top, {\mathbf{f}^2}^\top, {\mathbf{f}^3}^\top) (I_3 \otimes L_{\mathbb{S}}(f))
\begin{bmatrix}
\mathbf{f}^1\\
\mathbf{f}^2\\
\mathbf{f}^3
\end{bmatrix},
$$
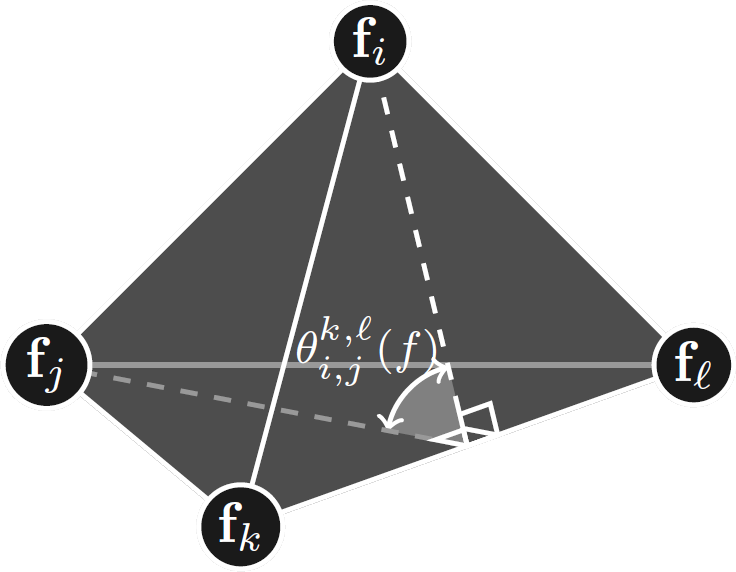
where $L_{\mathbb{S}}(f)$ is the stretched volumetric Laplacian matrix with
$\displaystyle
[L_{\mathbb{S}}(f)]_{i,j} =
\begin{cases}
-\frac{1}{6} \sum_{k, \ell} \frac{\left|[\mathbf{f}_{k}, \mathbf{f}_{\ell}]\right| \cot\theta_{i,j}^{k,\ell}({f})}{\color{yellow}{\frac{|[v_i, v_j, v_k, v_\ell]|}{|f([v_i, v_j, v_k, v_\ell])|}}} &\mbox{if $[{v}_i,{v}_j]\in\mathcal{E}(\mathcal{M})$,}\\
-\sum_{\ell\neq i} [L_{\mathbb{S}(f)}]_{i,\ell} &\mbox{if $j = i$,}\\
0 &\mbox{otherwise.}
\end{cases}
$
[YuLL19] Yueh, Li, Lin and Yau, SIAM J Imaging Sci, 12(2):1071–1098, 2019.
Lower Bound of Volumetric Stretch Energy
| Theorem [HuLL22] | The volumetric stretch energy satisfies $${E}_\mathbb{S}(f) \geq \frac{3}{2}|f(\mathcal{M})|.$$ The equality holds if and only if $f$ is volume-preserving. |
\begin{align*} E_\mathbb{S}(f) &= \frac{1}{2} \sum_{s=1}^3 \sum_{\tau=[v_i,v_j,v_k,v_\ell]\in\mathcal{T}(\mathcal{M})} \begin{bmatrix} f_i^s & f_j^s & f_k^s & f_\ell^s \end{bmatrix} [L_\mathbb{S}(f)]_{\tau} \begin{bmatrix} f_i^s \\ f_j^s \\ f_k^s \\ f_\ell^s \end{bmatrix} \\ &= \sum_{\tau\in\mathcal{T}(\mathcal{M})} \frac{3|f(\tau)|^2}{2|\tau|} \geq \frac{3}{2}\sum_{\tau\in\mathcal{T}(\mathcal{M})} |f(\tau)| = \frac{3}{2}|f(\mathcal{M})|. \end{align*} The equality holds if and only if $|f(\tau)| = |\tau|$, for every $\tau\in\mathcal{T}(\mathcal{M})$.
[HuLL22] Huang, Liao, Lin, Yueh and Yau, arXiv:2210.09654, 2022.
Gradient Formula of Volumetric Stretch Energy
| Proposition [HuLL22] | The gradient of $E_\mathbb{S}$ can be formulated as \begin{align*} \nabla_{\mathbf{f}^s} E_\mathbb{S}(f) &= 3 L_\mathbb{S}(f) \, \mathbf{f}^s, ~\text{for $s=1,2,3$.} \end{align*} |
$$ [\nabla_{\mathbf{f}^s} E_\mathbb{S}(f)]_\ell = [L_\mathbb{S}(f) \, \mathbf{f}^s]_\ell + \underbrace{\frac{1}{2} \sum_{t=1}^3 \sum_{i=1}^n \sum_{j=1}^n f_i^t f_j^t \frac{\partial}{\partial f_\ell^s}[L_\mathbb{S}(f)]_{i,j}}_{(*)}. $$ It suffices to check $(*) = 2 [L_\mathbb{S}(f) \, \mathbf{f}^s]_\ell$.
Fixed Point Iteration for VSEM
The critical point $f$ satisfies $L_\mathbb{S}(f) \, \mathbf{f}^s =\mathbf{0}$, for $s=1,2,3$. Under a given boundary constraint $\mathbf{f}^s_\mathtt{B} = \mathbf{g}^s$, the critical point $f$ satisfies $$ [L_\mathbb{S}(f)]_{\mathtt{I},\mathtt{I}} \mathbf{f}^s_{\mathtt{I}} = -[L_\mathbb{S}(f)]_{\mathtt{I},\mathtt{B}} \mathbf{g}^s. $$
Let \begin{equation} \varphi^s(f) = \begin{bmatrix} -[L_\mathbb{S}(f)]_{\mathtt{I},\mathtt{I}}^{-1} [L_\mathbb{S}(f)]_{\mathtt{I},\mathtt{B}} \mathbf{g}^s \\ \mathbf{g}^s \end{bmatrix}, ~\text{for $s=1,2,3$}. \end{equation}
| Algorithm [YuLL19] | $ {\mathbf{f}^s}^{(n+1)} = \varphi^s(f^{(n)}), ~ \text{for $s=1,2,3$}. $ |
[YuLL19] Yueh, Li, Lin and Yau, SIAM J Imaging Sci, 12(2):1071–1098, 2019.
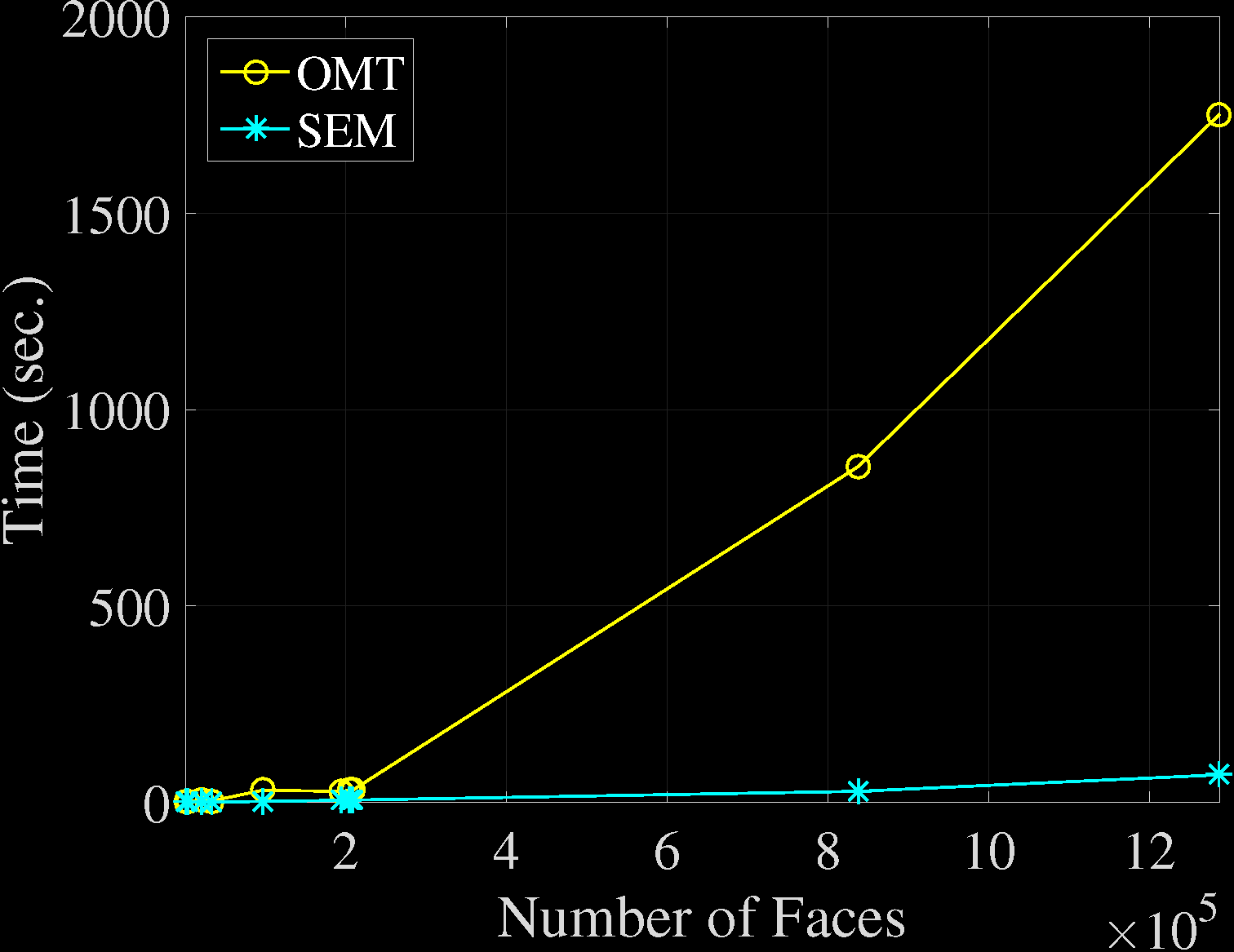
Application of VSEM to Optimal Mass Transportation
Optimal Mass Transportation (OMT) Problem
The OMT problem aims to find a measure-preserving map $f:\mathcal{M}\to \mathcal{N}$ that minimizes $$ \mathcal{C}(f) = \int_\mathcal{M} \| x - f(x)\|^2 \,\mathrm{d}\mu. $$
 $\xrightarrow{~~~~~f~~~~~}$
$\xrightarrow{~~~~~f~~~~~}$

$(\mathcal{M},\mu)$ $(\mathcal{N},\nu)$
Discrete OMT Problem
The discrete OMT problem aims to find a measure-preserving map $f:\mathcal{M}\to\mathcal{N}$ that minimizes $$ \mathcal{C}_V(f) = \sum_{v\in\mathcal{V}(\mathcal{M})} \|v - f(v)\|^2 \,\mu_V(v), ~ \text{where $\mu_V(v)=\frac{1}{4}\sum_{\tau\supset v} \mu(\tau)$.} $$
 $\xrightarrow{~~~~~f~~~~~}$
$\xrightarrow{~~~~~f~~~~~}$

Denote $\mathscr{F}:= \{f:\mathcal{M}\to\mathbb{B} \mid \text{$f$ is measure-preserving} \}.$
Projected Gradient Method for OMT Mappings [YuHL21]
| Brain Mesh | Initial | Gradient | Projection |
 |
 |
 |
 |
| Gradient: | $f^{(k+\frac12)} = f^{(k)} - \eta^{(k)} \nabla\mathcal{C}(f^{(k)}).$ |
| Projection: | $f^{(k+1)} = \Pi_{\mathscr{F}}(f^{(k+\frac12)})$ by the VSEM. |
[YuHL21] Yueh, Huang, Li, Lin and Yau, J Sci Comput, 88, 64, 2021.
Application to Brain Tumor Segmentation
Tumor Segmentation for 3D Brain Images
The raw data of BraTS / MSD is a tensor $A\in\mathbb{R}^{240\times240\times155\times4}$.
Goal Automatically segment pixels of tumor regions:
| FLAIR | T1 | T1CE | T2 |
Tumor Segmentation via the U-Net
U-Net is a convolution neural network for image segmentation.
Core Issue Raw images are too large to be input directly.
Observation Raw images contain lots of blank pixels.
| FLAIR | T1 | T1CE | T2 |
OMT for Image Processing
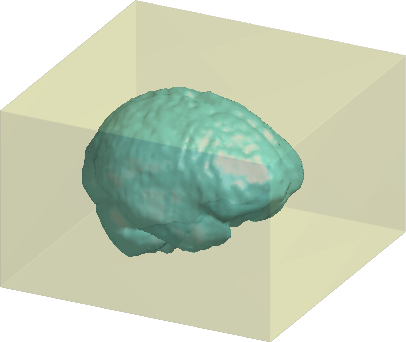 $\xrightarrow[]{\text{Sampling}}$
$\xrightarrow[]{\text{Sampling}}$
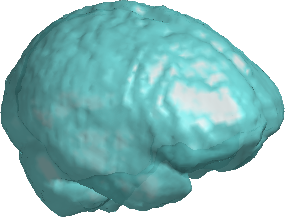 $\xrightarrow[]{\text{OMT}}$
$\xrightarrow[]{\text{OMT}}$

The OMT maps can help to:
1. Resample images and omit blank regions.
2. Reshape images in a memory-efficient manner.
Training with Unified Data [LiJY21] [LiLH22]
 $\xrightarrow[]{~~f_1~~}$
$\xrightarrow[]{~~f_1~~}$
 $\xleftarrow[]{~~f_2~~}$
$\xleftarrow[]{~~f_2~~}$

| Advantages: | 1. No waste of memory for the blank region. |
| 2. Controllable size of input tensors for the U-net. |
[LiJY21] Lin, Juang, Yueh, Huang, Li, Wang and Yau, Sci Rep, 11, 14686, 2021.
[LiLH22] Lin, Lin, Huang, Li, Yueh and Yau, Sci Rep, 12, 6452, 2022.
Segmentation Flowchart
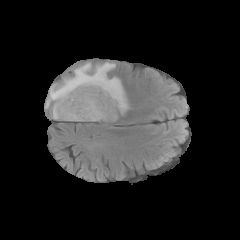 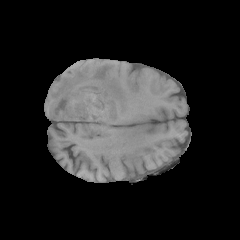 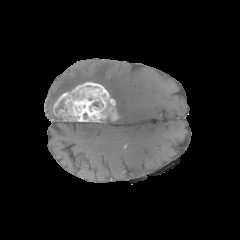 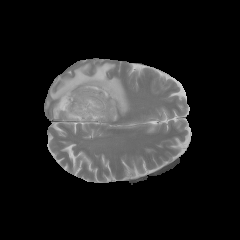
|
$\xrightarrow[]{\text{OMT}}$ |
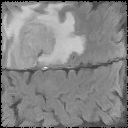 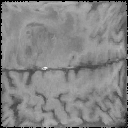  
|
$\xrightarrow[]{\text{U-Net}}$ |
|
$\xrightarrow[]{(\text{OMT})^{-1}}$ |
  
|
$\xrightarrow[]{\text{Merge}}$ |

|
Segmentation Accuracy [LiLH22]
| Validation | Whole Tumor | Tumor Core | Enhancing Tumor |
| Dice Score | 0.93705 | 0.90617 | 0.87470 |
Significance
Space Reduce data size by 76.5% while keeping a similar resolution.
Time Reduce time cost for training and inference for tumor regions.
[LiLH22] Lin, Lin, Huang, Li, Yueh and Yau, Sci Rep, 12, 6452, 2022.
These slides can be accessed at

http://tiny.cc/NTHU2022

