Another group action on left coset

�U�@��: Sylow p-subgroups ��Y �W�@��: Second Sylow's Theorem �e�@��: Second Sylow's Theorem

Another group action on left coset

�e�@�`�ҩ� First Sylow's Theorem �ڭ̬O�� H �� G �� H �� left coset �@��. �o�̧ڭ̦Ҽ{ H �� G ��O�@�� subgroup P �� left coset �@��.

�Y G �O�@�� finite group, H �M P �O G �� subgroups. �O S = {a^.P | a $\in$ G} �O G �� P �� left coset �Ҧ��X. �ڭ̩w�q H �� S ��@�Φp�U: ��N�� h $\in$ H, a^.P $\in$ S, �ڭ̩w�q

h*(a^.P) = (h^.a)^.P.

�Q�ΩM�e�@�`�ۦP��ҩ��i�� (H, S,*) �O�@�� group action. �P�˪��ڭ̤]��

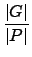| S| = $\displaystyle {\frac{\vert G\vert}{\vert P\vert}}$ .

(4.16)

�Ӥ��|�O S₀ �O? �Y a^.P $\in$ S₀, �h��Ҧ� h $\in$ H �Ҧ�

(h^.a)^.P = h*(a^.P) = a^.P.

�o�i�D�ڭ� a �M h^.a �b P ��U�O�P��, �]�N�O a^{-1 .}h^.a $\in$ P. �]��o�O��Ҧ�� h $\in$ H ��O�諸, �ڭ̥i�H�g�� a^{-1 .}H^.a $\subseteq$ P. �]��Y a^.P $\in$ S₀ �h�ڭ̦� a^{-1 .}H^.a $\subseteq$ P. �Ϥ�, �Y a �ŦX a^{-1 .}H^.a $\subseteq$ P, �h a^.P $\in$ S₀. �ҥH�ڭ̱o��

S₀ = {a^.P | a^{-1 .}H^.a 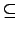$\displaystyle \subseteq$ P}.

(4.17)

�o�̧ڭ̭n��@�� (�M Sylow �w�z�L��u�O�n��M�[��). �Y�ڭ̦p�e�@�`�� G �� a �ŦX a^{-1 .}H^.a $\subseteq$ P ��@�Ӷ��X {a $\in$ G | a^{-1 .}H^.a $\subseteq$ P}. �o�@�Ӷ��X�ä��@�w�|�O G �� subgroup (�ʫʳ��), �ӥB P �]��|�]�t�� (��D H $\subseteq$ P). �ҥH�ڭ̨S��p�e��X�� group action �h�� | S₀| ��l. ��L�S��Y, �b�� Second Sylow's Theorem �ɧڭ̤��ݭn�� | S₀|.

�U�@��: Sylow p-subgroups ��Y �W�@��: Second Sylow's Theorem �e�@��: Second Sylow's Theorem

Administrator 2005-06-18