


下一頁: Third Sylow's Theorem
上一頁: Second Sylow's Theorem
前一頁: Another group action on
由第一 Sylow 定理我們可找到一個 G 的 Sylow p-subgroup. 第二
Sylow 定理告訴我們如何由這一個 Sylow p-subgroup, 得到所有 G 的
Sylow p-subgroup.
Theorem 4.5.1 (Second Sylow's Theorem)
令
p 是一質數. 若
G 是一個 finite group, 而
P 是
G 的一個
Sylow
p-subgroup.
- 若 H 是 G 的一個 p-subgroup, 則存在 a
 G 使得
G 使得
H 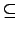 a . P . a-1
a . P . a-1.
- 若 P' 是 G 的另一個 Sylow
p-subgroup, 則存在 a
 G 使得
G 使得
P' = a . P . a-1.
証 明.
(1)
我們考慮前面所述
H 對
S = {
a . P |
a  G
G} 的 group action.
假設 |
G| =
pnm, 其中
p m
m. 因
P 是
G 的 Sylow
p-subgroup, 由定義知 |
P| =
pn. 故由式子 (
4.16) 知
|
S| = |
G|/|
P| =
m. 然而
p m
m, 故知
p 不能整除 |
S|, 也就是說
| S| 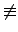 0(mod p). 0(mod p). |
(4.18) |
由假設
H 是一個
p-group, 故由 Proposition
4.1.4
和前一式子 (
4.18) 知
|
S0|
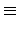
|
S|
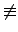
0(mod
p).
也就是說
p 不能整除 |
S0|. 這告訴我們
S0 是非空的集合; 否則
|
S0| = 0, 這和
p 不能整除 |
S0| 矛盾. 既然
S0 是非空的,
所以存在
a  G
G 使得
a . P  S0
S0. 故由式子 (
4.17)
知
a-1 . H . a  P
P. 這告訴我們
H  a . P . a-1
a . P . a-1.
(2) 當 P' 是 G 中另一個 Sylow p-subgroup, 我們直接套用 (1)
的結果知存在 a  G 使得
P'
G 使得
P'  a . P . a-1. 然而
Lemma 1.5.2 告訴我們
| P| = | a . P . a-1|, 且又由定義
| P'| = | P|, 故得
| P'| = | a . P . a-1|. 所以得證
P' = a . P . a-1.
a . P . a-1. 然而
Lemma 1.5.2 告訴我們
| P| = | a . P . a-1|, 且又由定義
| P'| = | P|, 故得
| P'| = | a . P . a-1|. 所以得證
P' = a . P . a-1. 
Theorem 4.5.1 告訴我們若在 G 找到一個 Sylow p-subgroup
P, 則所有的 Sylow p-subgroup 都是
a . P . a-1,
這種形式. 如果 P 剛好是 G 的一個 normal subgroup, 則知任意的
a  G 都符合
a . P . a-1 = P, 換句話說 G 只有一個
Sylow p-subgroup. 反之, 若 P 不是 G 的 normal subgroup,
則存在一個 a
G 都符合
a . P . a-1 = P, 換句話說 G 只有一個
Sylow p-subgroup. 反之, 若 P 不是 G 的 normal subgroup,
則存在一個 a  G 使得
a . P . a-1
G 使得
a . P . a-1 P. 然而 Lemma
1.5.2 告訴我們
a . P . a-1 是 G 的一個 subgroup,
且
| a . P . a-1| = | P|, 換句話說
a . P . a-1 是
G 中另一個不等於 P 的 Sylow p-subgroup. 故此時 Sylow
p-subgroup 並不唯一. 我們證得:
P. 然而 Lemma
1.5.2 告訴我們
a . P . a-1 是 G 的一個 subgroup,
且
| a . P . a-1| = | P|, 換句話說
a . P . a-1 是
G 中另一個不等於 P 的 Sylow p-subgroup. 故此時 Sylow
p-subgroup 並不唯一. 我們證得:
Corollary 4.5.2
若
P 是
G 的一個 Sylow
p-subgroup, 則
G 僅有一個 Sylow
p-subgroup 若且為若
P 是
G 的 normal subgroup.
Example 4.5.3
我們知
|
A4| = 4!/2 = 2
2 . 3. 我們考慮
A4 的 Sylow 2-subgroup
和 Sylow 3-subgroup. 已知
A4 中有一個 order 4 的 normal
subgroup
N = {I,(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)}.
因為
N 是
A4 的 Sylow 2-subgroup, 故知
A4 中不會有其他 order 為
4 的 subgroup. 而
(1 2 3) 在
A4 中產生的 cyclic
subgroup 是 order 3, 故

(1 2 3)

是
A4
的一個 Sylow 3-subgroup. 同理

(1 2 4)

是另一個 Sylow 3-subgroup. 所以知

(1 2 3)

不可能是
A4 的 normal subgroup.



下一頁: Third Sylow's Theorem
上一頁: Second Sylow's Theorem
前一頁: Another group action on
Administrator
2005-06-18
 G 使得
H
G 使得
H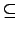 a . P . a-1.
a . P . a-1.
 G 使得
P' = a . P . a-1.
G 使得
P' = a . P . a-1.![]() G 使得
P'
G 使得
P' ![]() a . P . a-1. 然而
Lemma 1.5.2 告訴我們
| P| = | a . P . a-1|, 且又由定義
| P'| = | P|, 故得
| P'| = | a . P . a-1|. 所以得證
P' = a . P . a-1.
a . P . a-1. 然而
Lemma 1.5.2 告訴我們
| P| = | a . P . a-1|, 且又由定義
| P'| = | P|, 故得
| P'| = | a . P . a-1|. 所以得證
P' = a . P . a-1. ![]()
![]() G 都符合
a . P . a-1 = P, 換句話說 G 只有一個
Sylow p-subgroup. 反之, 若 P 不是 G 的 normal subgroup,
則存在一個 a
G 都符合
a . P . a-1 = P, 換句話說 G 只有一個
Sylow p-subgroup. 反之, 若 P 不是 G 的 normal subgroup,
則存在一個 a ![]() G 使得
a . P . a-1
G 使得
a . P . a-1![]() P. 然而 Lemma
1.5.2 告訴我們
a . P . a-1 是 G 的一個 subgroup,
且
| a . P . a-1| = | P|, 換句話說
a . P . a-1 是
G 中另一個不等於 P 的 Sylow p-subgroup. 故此時 Sylow
p-subgroup 並不唯一. 我們證得:
P. 然而 Lemma
1.5.2 告訴我們
a . P . a-1 是 G 的一個 subgroup,
且
| a . P . a-1| = | P|, 換句話說
a . P . a-1 是
G 中另一個不等於 P 的 Sylow p-subgroup. 故此時 Sylow
p-subgroup 並不唯一. 我們證得: