下一頁: Zero Divisor 和 Unit 上一頁: 初級 Ring 的性質 前一頁: Ring 的基本定義

由 Ring 的定義所得的性質

在這節中我們介紹一些直接用 ring 的定義 (尤其是分配率) 就可推得的基本性質.

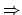若 R 是一個 ring, 其加法的 identity 我們曾經提過習慣上是用 0 來表示. 雖然這一個 0 並非大家熟悉的那個 0 不過就因為它和大家熟悉的 0 有貧共通的性質, 所以我們用 0 來表示它. 哪些共通的性質呢? 除了 a + 0 = 0 與 a + x = a $\Rightarrow$ x = 0 � , 以下的 Lemma 大家應也很熟悉吧!

Lemma 5.2.1 若 R 是一個 ring 且 0 是其加法的 identity, 則對任意的 a $\in$ R 皆有

a^.0 = 0^.a = 0.

証明. 大家應可以觀察出 0 是和加法有關的, 而 a^.0 又和乘法有關, 所以不難想像這個 Lemma 一定和分配率有關.

由於 0 是加法的 identity, 故由 (R3) 知 0 + 0 = 0. 因此由 (R8) 得:

a^.0 = a^.(0 + 0) = a^.0 + a^.0.

然而由 (R3) 知: a^.0 + 0 = a^.0, 也就是說 x = 0 和 x = a^.0 皆為 a^.0 + x = a^.0 的解. 故利用 Lemma 5.1.2 (2) 可知 a^.0 = 0.

同理利用 (0 + 0)^.a = 0^.a 可得 0^.a = 0. $\qedsymbol$

Remark 5.2.2 有的同學或逖利用

a^.0 = a^.(a - a) = a^.a - a^.a = 0

(5.1)

這一個等式來證明 Lemma 5.2.1. 式子 (5.1) 其實是有問題的. 問題發生在 R 中並沒有「-」這一個運算. 換句話說大家習慣寫的 0 = a - a 應該寫成 0 = a + (- a). 因此式子 (5.1) 應該改寫成

a^.0 = a^.(a + (- a)) = a^.a + a^.(- a).

然而 a^.a + a^.(- a) 會等於 0 嗎? 若是 0 就表示 a^.(- a) 應該是 a^.a 的加法 inverse, 也就是 a^.(- a) = - (a^.a). 這一點到目前為止我們還不知道是對還是錯 (見 Lemma 5.2.3). 所以這並不能證明 Lemma 5.2.1.

到底我們熟悉的 a^.(- a) = - (a^.a) 對嗎? 下一個 Lemma 告訴我們其實是對的.

Lemma 5.2.3 若 R 是一個 ring, 則對任意的 a, b $\in$ R 皆有

a^.(- b) = (- a)^.b = - (a^.b).

証明. 首先分清楚 a^.(- b) 是 a 乘上 b 的加法 inverse, - a^.b 是 a 的加法 inverse 乘上 b 而 - (a^.b) 是 a^.b 的加法 inverse. 所以要證明 a^.(- b) = - (a^.b) 我們只要證明 (a^.(- b)) + (a^.b) = 0. 然而利用 (R8) 和 Lemma 5.2.1 知

(a^.(- b)) + (a^.b) = a^.((- b) + b) = a^.0 = 0,

故得證. 同理可得 (- a)^.b = - (a^.b). $\qedsymbol$

在一般的 ring, R 中 - a 不一定可以寫成 (- 1)^.a. 主要的原因是 1 不一定在 R 中, 所以 -1 不一定在 R 中. 因此有可能在 R 中 (- 1)^.a 是沒有意義的. 不過如果 R 是一個 ring with 1, 則利用 Lemma 5.2.3 我們確實可得

(- 1)^.a = 1^.(- a) = - a 且 a^.(- 1) = - (a^.1) = - a.

利用 Lemma 5.2.3 我們可以得到以下大家熟悉的等式.

Corollary 5.2.4 若 R 是一個 ring 且 a, b $\in$ R 則

(- a)^.(- b) = a^.b.

証明. 先把 - b 看成是一元素, 故利用 Lemma 5.2.3 可得 (- a)^.(- b) = - (a^.(- b)). 然而在套用一次 Lemma 5.2.3 得 a^.(- b) = - (a^.b). 結合以上二等式得

(- a)^.(- b) = - (- (a^.b)).

最後利用 Lemma 5.1.2 (1) 知 - (- (a^.b)) = a^.b, 故得證 (- a)^.(- b) = a^.b. $\qedsymbol$

由 Lemma 5.2.3 和 Corollary 5.2.4 我們知道「-」的運算和我們一般熟悉的運算相同, 以後我們將依習慣將 a + (- b) 寫成 a - b.

大家初次看到 ring 的定義時或逖疑惑加法的結構中為何要求是一個 abelian group? 事實上如果當初僅要求加法是一個 group 但乘法有 identity 1, 則這會`強迫' R 在加法之下是一個 abelian group. 這是因為對任意的 a, b $\in$ R, 考� (a + b)^.(1 + 1) 我們會有以下兩個等式:

(a + b)^.(1 + 1) = a^.(1 + 1) + b^.(1 + 1) = (a + a) + (b + b),

(a + b)^.(1 + 1) = (a + b)^.1 + (a + b)^.1 = (a + b) + (a + b).

也就是說 a + a + b + b = a + b + a + b, 故可得 a + b = b + a.

最後我們要注意的是: 當 n 是一個正整數時, 為了方便一般我們會習慣用 na 來表示 n 個 a 相加所得之值. 例如 2a = a + a, 3a = a + a + a, ...等. 不過千萬不要把 2a 寫成 2^.a, na 寫成 n^.a. 這是因為 2 或是其他的 n 不一定會在 R 中, 所以 n 和 a 是不能相乘的. 那麼對任意的正整數 n 和 m, 我們一般熟悉的 (na)^.(mb) = (nm)(a^.b) 會對嗎? 這是沒有問題的, 你將 na 寫成 n 個 a 相加, mb 寫成 m 個 b 相加, 再利用分配率 (R8) 自然可的 nm 個 a^.b 相加.

下一頁: Zero Divisor 和 Unit 上一頁: 初級 Ring 的性質 前一頁: Ring 的基本定義

Administrator 2005-06-18