

下一頁: The Möbius Inversion Formula
上一頁: Arithmetic Function
前一頁: The Euler -function
我們可以利用 convolution 定義出新的 multiplicative arithmetic
function, 另外 convolution
也提供了一個較簡明的方法來證明下一節要探討的 Möbius inversion
formula. 雖然本節及下一節的內容在本講義中以後不會用到,
但希望利用此介紹讓大家知道有時適當定義一些運算對解決問題有很大的幫助.
Definition 2.4.1
給定兩 arithmetic functions
f,
g 我們記其
convolution 為
f*
g, 其定義為對任意
n 

,
f*
g(
n) =
 f
f (
d )
g(
n/
d ).
依照 convolution 的定義, 要求 f*g(n) 之值, 首先找出 n
的所有正因數, 然後對於每一個 n 的正因數 d, 我們求
f (d )g(n/d )
之值, 再將這些值加起來. 若 d 是 n 的正因數, 令 e = n/d,
我們自然有 de = n. 反之, 若 d, e 是正整數滿足 de = n, 則我們自然有
d| n. 因此我們也可以用如下的表示法表示 f*g. 即,
f*
g(
n) =
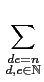 f
f (
d )
g(
e).
這樣的表示法雖然看來像兩個變數, 但實質上若給定 d, 則
e 自然確定. 我們選用這個表示法是因為底下要推導 convolution
的性質時用這種表法較簡明.
由於 f 和 g 是 arithmetic function, 所以 f*g
在任意正整數皆有取值, 因此 f*g 仍為 arithmetic function. 換言之
convolution 可以看成是一個 arithmetic function 之間的運算
(你可以將它看成是兩個 arithmetic function 之間的乘法).
接下來我們就是要探討這種運算的基本性質.
Proposition 2.4.2
設
f,
g,
h 皆為 arithmetic function. 令
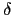
:


定義為
關於 convolution 我們有以下之性質.
-
f*
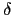 =
= 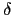 *f = f.
*f = f.
- f*g = g*f.
-
(f*g)*h = f*(g*h).
証 明.
(1) 依定義對任意
n 

,
f*
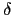
(
n) =
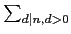 f
f (
d )
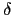
(
n/
d ). 由於當
n/
d > 1 時
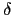
(
n/
d )= 0. 因此在
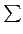
內, 只有
d =
n 這一項留下, 故得
f*
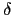
(
n) =
f (
n)
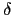
(1) =
f (
n). 換言之,
f 和
f*
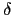
在任意
n 

的取值皆相同. 故從函數的觀點來看, 它們是相同的函數.
同理可證
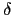
*
f =
f.
(2) 由於對任意
n 
 ,
,
f*
g(
n) =
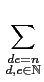 f
f (
d )
g(
e) =
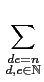 g
g(
e)
f (
d )=
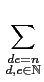 g
g(
d )
f (
e) =
g*
f (
n).
我們得證
f*
g =
g*
f.
(3) 依定義, 對任意
n 
 ,
,
| (f*g)*h(n) |
= |
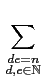 (f*g)(d )h(e) (f*g)(d )h(e) |
|
| |
= |
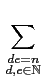 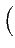  f (r)g(s) f (r)g(s)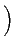 h(e) h(e) |
|
| |
= |
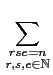 f (r)g(s)h(e). f (r)g(s)h(e). |
|
同理我們有
f*(
g*
h)(
n) =
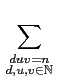 f
f (
d )
g(
u)
h(
v).
因此得證
(
f*
g)*
h =
f*(
g*
h).

Proposition 2.4.2 告訴我們, 若將 * 看成是 arithmetic
function 之間的運算, 則 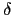 這一個 arithmetic function
就如同乘法運算的 1 (這樣的元素, 我們稱之為 identity). 而且 *
這個運算滿足交換率以及結合率. * 這個運算其實對於 multiplicative
arithmetic function 也具有封閉性. 也就是說我們有以下之性質.
這一個 arithmetic function
就如同乘法運算的 1 (這樣的元素, 我們稱之為 identity). 而且 *
這個運算滿足交換率以及結合率. * 這個運算其實對於 multiplicative
arithmetic function 也具有封閉性. 也就是說我們有以下之性質.
Theorem 2.4.3
假設
f,
g 皆為 multiplicative arithmetic function, 則
f*
g 也是
multiplicative arithmetic function.
証 明.
假設
a,
b 

且
gcd(
a,
b) = 1, 我們要證明
f*
g(
ab) = (
f*
g(
a))(
f*
g(
b)). 對任意
d,
e 

滿足
de =
ab,
我們皆有
d|
ab 且
e|
ab. 依 Lemma
2.1.4
知分別存在唯一的一組
d1,
d2 以及
e1,
e2 滿足
d =
d1d2 及
e =
e1e2 其中
d1,
e1 為
a 的正因數 且
d2,
e2 為
b
的正因數. 又因
gcd(
a,
b) = 1, 故
gcd(
d1,
d2) = 1 且
gcd(
e1,
e2) = 1. 所以由
f,
g 是 multiplicative 以及定義知
f*
g(
ab) =
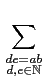 f
f (
d )
g(
e) =
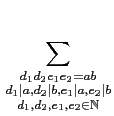 f
f (
d1)
f (
d2)
g(
e1)
g(
e2).
現對任意
d1, d2, e1, e2 
 滿足
d1d2e1e2 = ab 且 d1, e1
和 d2, e2 分別是 a 和 b 的因數. 因為 d1e1| ab, 又因
gcd(a, b) = 1 且 d1, e1 是 a 的因數, 知
gcd(d1e1, b) = 1.
因此由 Proposition 1.2.7(1) 知 d1e1| a. 另一方面
a| d1e1d2e2, 再由
gcd(a, b) = 1 以及 d2, e2 為 b 之因數,
得
gcd(a, d2e2) = 1. 因此知 a| d1e1. 所以得證 a = d1e1,
同理得證 b = d2e2. 反之, 若
d1, d2, e1, e2
滿足
d1d2e1e2 = ab 且 d1, e1
和 d2, e2 分別是 a 和 b 的因數. 因為 d1e1| ab, 又因
gcd(a, b) = 1 且 d1, e1 是 a 的因數, 知
gcd(d1e1, b) = 1.
因此由 Proposition 1.2.7(1) 知 d1e1| a. 另一方面
a| d1e1d2e2, 再由
gcd(a, b) = 1 以及 d2, e2 為 b 之因數,
得
gcd(a, d2e2) = 1. 因此知 a| d1e1. 所以得證 a = d1e1,
同理得證 b = d2e2. 反之, 若
d1, d2, e1, e2 
 滿足
a = d1e1 且 b = d2e2, 則我們有
d1d2e1e2 = ab 且 d1, e1 和
d2, e2 分別是 a 和 b 的因數. 因此我們有
滿足
a = d1e1 且 b = d2e2, 則我們有
d1d2e1e2 = ab 且 d1, e1 和
d2, e2 分別是 a 和 b 的因數. 因此我們有
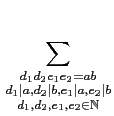 f
f (
d1)
f (
d2)
g(
e1)
g(
e2) =
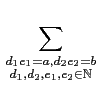 f
f (
d1)
f (
d2)
g(
e1)
g(
e2).
另一方面
(
f*
g(
a))(
f*
g(
b)) =
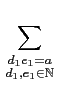 f
f (
d1)
g(
e1)
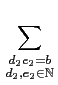 f
f (
d2)
g(
e2).
利用分配率知
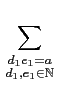 f
f (
d1)
g(
e1)
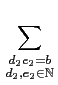 f
f (
d2)
g(
e2) =
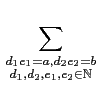 f
f (
d1)
f (
d2)
g(
e1)
g(
e2).
因此得證本定理.

若令
l : 
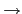
 是一個 arithmetic function 滿足對任意
n
是一個 arithmetic function 滿足對任意
n 
 ,
l(n) = 1, 則對任意的 arithmetic function f, 皆有當
n
,
l(n) = 1, 則對任意的 arithmetic function f, 皆有當
n 
 時,
時,
f*
l(
n) =
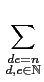 f
f (
d )
l(
e) =
 f
f (
d ).
因為
l 是一個 multiplicative arithmetic function, 從這個角度看
Theorem 2.1.5 只是 Theorem 2.4.3 的一個特殊情況.
Example 2.4.4
我們可以利用 Theorem
2.4.3 來求對任意
n 

,
之值, 其中

為 Möbius

-function (參見 Example
2.1.2).
令
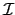 :
: 
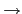
 是一個 arithmetic function 滿足對任意
n
是一個 arithmetic function 滿足對任意
n 
 ,
,
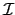 (n) = n. 考慮
F :
(n) = n. 考慮
F : 
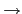
 是一個 arithmetic function
滿足對任意
n
是一個 arithmetic function
滿足對任意
n 
 ,
,
依定義我們知
F =

*
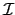
. 然而

和
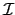
皆為 multiplicative,
故利用 Theorem
2.4.3 知
F 也是 multiplicative.
因此我們只要檢視對任意質數
p 以及
t 

,
F(
pt) 之值為何.
依定義

(1) = 1,

(
p) = - 1 且當
i > 1 時

(
pi) = 0, 故得
F(
pt) =
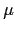
(1)
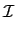
(
pt) +
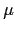
(
p)
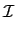
(
pt - 1) =
pt -
pt - 1.
注意此和
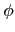
(
pt) 的值相同 (參見 Proposition
2.3.5), 故利用
F 和
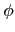
皆為 multiplicative 以及 Proposition
2.1.3 知
F =
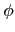
.
也就是說對任意
n 

皆有

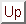

下一頁: The Möbius Inversion Formula
上一頁: Arithmetic Function
前一頁: The Euler -function
Li
2007-06-28
 f (d )g(n/d ).
f (d )g(n/d ).
 f (d )g(n/d ).
f (d )g(n/d ).
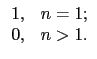
![]()
![]() ,
,
![]()
![]() ,
, 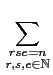 f (r)g(s)h(e).
f (r)g(s)h(e).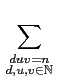 f (d )g(u)h(v).
f (d )g(u)h(v).
![]() 這一個 arithmetic function
就如同乘法運算的 1 (這樣的元素, 我們稱之為 identity). 而且 *
這個運算滿足交換率以及結合率. * 這個運算其實對於 multiplicative
arithmetic function 也具有封閉性. 也就是說我們有以下之性質.
這一個 arithmetic function
就如同乘法運算的 1 (這樣的元素, 我們稱之為 identity). 而且 *
這個運算滿足交換率以及結合率. * 這個運算其實對於 multiplicative
arithmetic function 也具有封閉性. 也就是說我們有以下之性質.
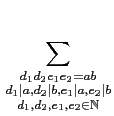 f (d1)f (d2)g(e1)g(e2).
f (d1)f (d2)g(e1)g(e2).
![]()
![]() 滿足
d1d2e1e2 = ab 且 d1, e1
和 d2, e2 分別是 a 和 b 的因數. 因為 d1e1| ab, 又因
gcd(a, b) = 1 且 d1, e1 是 a 的因數, 知
gcd(d1e1, b) = 1.
因此由 Proposition 1.2.7(1) 知 d1e1| a. 另一方面
a| d1e1d2e2, 再由
gcd(a, b) = 1 以及 d2, e2 為 b 之因數,
得
gcd(a, d2e2) = 1. 因此知 a| d1e1. 所以得證 a = d1e1,
同理得證 b = d2e2. 反之, 若
d1, d2, e1, e2
滿足
d1d2e1e2 = ab 且 d1, e1
和 d2, e2 分別是 a 和 b 的因數. 因為 d1e1| ab, 又因
gcd(a, b) = 1 且 d1, e1 是 a 的因數, 知
gcd(d1e1, b) = 1.
因此由 Proposition 1.2.7(1) 知 d1e1| a. 另一方面
a| d1e1d2e2, 再由
gcd(a, b) = 1 以及 d2, e2 為 b 之因數,
得
gcd(a, d2e2) = 1. 因此知 a| d1e1. 所以得證 a = d1e1,
同理得證 b = d2e2. 反之, 若
d1, d2, e1, e2 ![]()
![]() 滿足
a = d1e1 且 b = d2e2, 則我們有
d1d2e1e2 = ab 且 d1, e1 和
d2, e2 分別是 a 和 b 的因數. 因此我們有
滿足
a = d1e1 且 b = d2e2, 則我們有
d1d2e1e2 = ab 且 d1, e1 和
d2, e2 分別是 a 和 b 的因數. 因此我們有
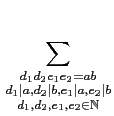 f (d1)f (d2)g(e1)g(e2) =
f (d1)f (d2)g(e1)g(e2) = 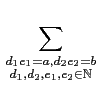 f (d1)f (d2)g(e1)g(e2).
f (d1)f (d2)g(e1)g(e2).
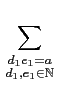 f (d1)g(e1)
f (d1)g(e1)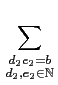 f (d2)g(e2).
f (d2)g(e2).
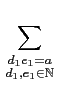 f (d1)g(e1)
f (d1)g(e1)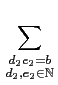 f (d2)g(e2) =
f (d2)g(e2) = 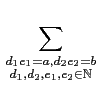 f (d1)f (d2)g(e1)g(e2).
f (d1)f (d2)g(e1)g(e2).
![]()
![]()
![]() 是一個 arithmetic function 滿足對任意
n
是一個 arithmetic function 滿足對任意
n ![]()
![]() ,
l(n) = 1, 則對任意的 arithmetic function f, 皆有當
n
,
l(n) = 1, 則對任意的 arithmetic function f, 皆有當
n ![]()
![]() 時,
時,
 f (d ).
f (d ).

![]() :
: ![]()
![]()
![]() 是一個 arithmetic function 滿足對任意
n
是一個 arithmetic function 滿足對任意
n ![]()
![]() ,
,
![]() (n) = n. 考慮
F :
(n) = n. 考慮
F : ![]()
![]()
![]() 是一個 arithmetic function
滿足對任意
n
是一個 arithmetic function
滿足對任意
n ![]()
![]() ,
,


