大家看到這樣的方程式, 首先會想到用配方法來解. 沒錯,
我們也是要用配方法. 不過這裡有一點要特別注意,
就是我們都是在整數的情況, 所以須避免用到除法. 例如大家要解
ax2 + bx + c = 0 時, 第一個想到的是將 x2 項的係數 a 除去得
x2 + (b/a)x + (c/a) = 0. 由於我們在談 congruence equation,
多項式需要求為整係數, 這個方法就行不通了 (除非 a| b 且 a| c).
當然了, 當 a 和 m 互質時存在
e ![]()
![]() 使得
ae
使得
ae ![]() 1(mod m), 所以此時我們可以將
ax2 + bx + c
1(mod m), 所以此時我們可以將
ax2 + bx + c ![]() 0(mod m) 兩邊乘上
e 而得
x2 + bex + ce
0(mod m) 兩邊乘上
e 而得
x2 + bex + ce ![]() 0(mod m). 不過這個方法要限制在
gcd(m, a) = 1 的情形, 而我們要探討的是一般情況,
所以我們需想辦法處理. 不管怎樣為了讓多項式為整係數,
我們不要用除的方法, 儘量用乘的. 所以為了使用配方法我們可以讓 x2
項係數成為完全平方, 也就是將
ax2 + bx + c
0(mod m). 不過這個方法要限制在
gcd(m, a) = 1 的情形, 而我們要探討的是一般情況,
所以我們需想辦法處理. 不管怎樣為了讓多項式為整係數,
我們不要用除的方法, 儘量用乘的. 所以為了使用配方法我們可以讓 x2
項係數成為完全平方, 也就是將
ax2 + bx + c ![]() 0(mod m) 兩邊乘上
a 而得
(ax)2 + abx + ac
0(mod m) 兩邊乘上
a 而得
(ax)2 + abx + ac ![]() 0(mod m). 接著處理 x 項係數,
由於不能用除的所以不能將 abx 寫成 2(ab/2)x, 但用配方法 x
項係數需偶數, 因此好的方法是將原式兩邊乘以 2.
不過這樣一來又破壞了原先 x2 項係數為完全平方的好處,
所以我們再多乘一個 2 使得 x2 項係數仍為完全平方.
0(mod m). 接著處理 x 項係數,
由於不能用除的所以不能將 abx 寫成 2(ab/2)x, 但用配方法 x
項係數需偶數, 因此好的方法是將原式兩邊乘以 2.
不過這樣一來又破壞了原先 x2 項係數為完全平方的好處,
所以我們再多乘一個 2 使得 x2 項係數仍為完全平方.
也就是說, 在解
ax2 + bx + c ![]() 0(mod m) 時我們可以將兩邊乘上 4a
使得原式成為
4a2x2 + 4abx + 4ac = (2ax)2 + 2(2ax)b + 4ac
0(mod m) 時我們可以將兩邊乘上 4a
使得原式成為
4a2x2 + 4abx + 4ac = (2ax)2 + 2(2ax)b + 4ac ![]() 0(mod m). 接下來就可用配方法常用步驟將式子寫成
(2ax + b)2
0(mod m). 接下來就可用配方法常用步驟將式子寫成
(2ax + b)2 ![]() b2 - 4ac(mod m). 因此我們將問題簡化成解
y2
b2 - 4ac(mod m). 因此我們將問題簡化成解
y2 ![]() b2 - 4ac(mod m). 今若沒有整數 k 滿足
k2
b2 - 4ac(mod m). 今若沒有整數 k 滿足
k2 ![]() b2 - 4ac(mod m),
那麼我們便知原 congruence equation,
ax2 + bx + c
b2 - 4ac(mod m),
那麼我們便知原 congruence equation,
ax2 + bx + c ![]() 0(mod m)
無解. 若可找到
k
0(mod m)
無解. 若可找到
k ![]()
![]() 滿足
k2
滿足
k2 ![]() b2 - 4ac(mod m),
那麼我們便可依前面探討一次的 congruence equation 的方法解
2ax + b
b2 - 4ac(mod m),
那麼我們便可依前面探討一次的 congruence equation 的方法解
2ax + b ![]() k(mod m), 而得到
ax2 + bx + c
k(mod m), 而得到
ax2 + bx + c ![]() 0(mod m)
解之情況.
0(mod m)
解之情況.
總之, 解二次 congruence equation,
ax2 + bx + c ![]() 0(mod m)
的問題, 可化簡成解
y2
0(mod m)
的問題, 可化簡成解
y2 ![]() d(mod m) 其中 d = b2 - 4ac.
因此我們接下來僅探討
x2
d(mod m) 其中 d = b2 - 4ac.
因此我們接下來僅探討
x2 ![]() a(mod m) 這樣的 congruence
equation.
a(mod m) 這樣的 congruence
equation.
假設
m = p1n1 ... ptnr, 其中這些 pi 為相異質數. 由
Corollary 4.4.3 知,
x2 ![]() a(mod m)
有解若且唯若對所有的 pi,
x2
a(mod m)
有解若且唯若對所有的 pi,
x2 ![]() a(mod pini) 有解.
因此我們又將問題化簡為求
x2
a(mod pini) 有解.
因此我們又將問題化簡為求
x2 ![]() a(mod pn), 其中 p 為質數且
n
a(mod pn), 其中 p 為質數且
n ![]()
![]() 的情形.
的情形.
我們來看一個綜合以上結果的例子.
接著因為
45 = 32×5, 我們可以將式子轉化成解
(13x + 15)2 ![]() 19(mod 9) 及
(13x + 15)2
19(mod 9) 及
(13x + 15)2 ![]() 19(mod 5). 也就是說分別解
(4x + 6)2
19(mod 5). 也就是說分別解
(4x + 6)2 ![]() 1(mod 9) 以及
(3x)2
1(mod 9) 以及
(3x)2 ![]() 4(mod 5). 由於
y
4(mod 5). 由於
y ![]() ±1(mod 9) 為
y2
±1(mod 9) 為
y2 ![]() 1(mod 9) 之解, 故知
4x + 6
1(mod 9) 之解, 故知
4x + 6 ![]() ±1(mod 9), 解得
x
±1(mod 9), 解得
x ![]() 1, 5(mod 9) 為
(13x + 15)2
1, 5(mod 9) 為
(13x + 15)2 ![]() 19(mod 9) 之解. 另一方面
y
19(mod 9) 之解. 另一方面
y ![]() ±2(mod 5)
為
y2
±2(mod 5)
為
y2 ![]() 4(mod 5) 之解, 故得
3x
4(mod 5) 之解, 故得
3x ![]() ±2(mod 5), 解得
x
±2(mod 5), 解得
x ![]() 1, 4(mod 5) 為
(13x2 + 15)2
1, 4(mod 5) 為
(13x2 + 15)2 ![]() 19(mod 5) 之解.
19(mod 5) 之解.
最後要解
29x2 + 15x + 1 ![]() 0(mod 45), 由前知 x 需符合:
0(mod 45), 由前知 x 需符合:
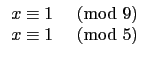 ,(2)
,(2)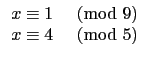 ,
,
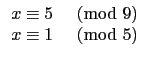 或 (4)
或 (4)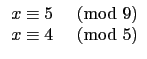 .
.
回到我們的主題. 我們將要解一般二次的 congruence equation 化解成解
x2 ![]() a(mod pn), 其中 p 為質數且
n
a(mod pn), 其中 p 為質數且
n ![]()
![]() 的情形.
我們先來看 a 和 p 不互質的情形. 假設 pn| a 等於解
x2
的情形.
我們先來看 a 和 p 不互質的情形. 假設 pn| a 等於解
x2 ![]() 0(mod pn), 此時當然有解. 若 a = pia' 其中 p
0(mod pn), 此時當然有解. 若 a = pia' 其中 p![]() a' 且
1
a' 且
1![]() i
i![]() n - 1 怎麼辦? 現假若 i 是奇數, 我們要說明此時
x2
n - 1 怎麼辦? 現假若 i 是奇數, 我們要說明此時
x2 ![]() pia'(mod pn) 無解. 若有解且 b 為
x2
pia'(mod pn) 無解. 若有解且 b 為
x2 ![]() pia'(mod pn) 之一解, 我們將 b 寫成 b = psb', 其中 p
pia'(mod pn) 之一解, 我們將 b 寫成 b = psb', 其中 p![]() b'. 此時因假設
b2
b'. 此時因假設
b2 ![]() pia'(mod pn), 可得
pn| p2sb'2 - pia'. 由於 2s 是偶數而 i 是奇數, 知 2s
pia'(mod pn), 可得
pn| p2sb'2 - pia'. 由於 2s 是偶數而 i 是奇數, 知 2s![]() i.
如果 2s > i, 則
p2sb'2 - pia' = pi(p2s - ib'2 - a'). 但由於
p| p2s - i 且 p
i.
如果 2s > i, 則
p2sb'2 - pia' = pi(p2s - ib'2 - a'). 但由於
p| p2s - i 且 p![]() a', 我們知
p
a', 我們知
p![]() p2s - ib'2 - a'. 換言之
pi + 1
p2s - ib'2 - a'. 換言之
pi + 1![]() p2sb'2 - pia'. 此和
pn| p2sb'2 - pia' 且
n
p2sb'2 - pia'. 此和
pn| p2sb'2 - pia' 且
n![]() i + 1 相矛盾. 同理, 若 2s < i, 我們也可得矛盾的情形. 所以當
i < n 且是奇數時
x2
i + 1 相矛盾. 同理, 若 2s < i, 我們也可得矛盾的情形. 所以當
i < n 且是奇數時
x2 ![]() pia'(mod pn) 無解.
pia'(mod pn) 無解.
當 a = pia' 其中 p![]() a', 0 < i < n 且 i = 2k 是偶數時, 若我們將
x 寫成 x = pkt, 此時解
x2
a', 0 < i < n 且 i = 2k 是偶數時, 若我們將
x 寫成 x = pkt, 此時解
x2 ![]() a(mod pn) 等同於解
(pkt)2
a(mod pn) 等同於解
(pkt)2 ![]() p2ka'(mod pn), 也就是解
p2kt2
p2ka'(mod pn), 也就是解
p2kt2 ![]() p2ka'(mod pn). 由於 2k < n, Proposition 4.2.1
告訴我們此式等同於解
t2
p2ka'(mod pn). 由於 2k < n, Proposition 4.2.1
告訴我們此式等同於解
t2 ![]() a'(mod pn - 2k).
我們將以上討論寫成結論.
a'(mod pn - 2k).
我們將以上討論寫成結論.
從以上的討論我們知道要解一個二次的 congruence equation 都可以簡化到
x2 ![]() a(mod pn), 其中 p
a(mod pn), 其中 p![]() a 的情況.
所以以後我們僅專注於
x2
a 的情況.
所以以後我們僅專注於
x2 ![]() a(mod pn) 其中 p
a(mod pn) 其中 p![]() a 的情形.
a 的情形.