

下一頁: 質數
上一頁: 整數的基本性質
前一頁: 除法原理
輾轉相除法是求最大公因數很有效率的方法.
首先我們介紹輾轉相除法的原理.
Lemma 1.3.1
若
a,
b 

且
a =
bh +
r, 其中
h,
r 

, 則
gcd(
a,
b) = gcd(
b,
r).
証 明.
假設
d1 = gcd(
a,
b) 且
d2 = gcd(
b,
r). 我們證明
d1|
d2 且
d2|
d1, 因而可利用 Proposition
1.1.3(2) 以及
d1,
d2
皆為正數得證
d1 =
d2.
因 d1| a 且 d1| b 利用 Corollary 1.1.2 我們知
d1| a - bh = r. 因為 d1| b, d1| r 且
d2 = gcd(b, r) 故由
Proposition 1.2.5 知 d1| d2. 另一方面, 因為 d2| b 且
d2| r 故
d2| bh + r = a. 因此可得 d2| d1.

Lemma 1.3.1 告訴我們當 a > b > 0 時, 要求 a, b
的最大公因數我們可以先將 a 除以 b 所得餘數若為 r, 則 a, b
的最大公因數等於 b 和 r 的最大公因數. 因為
0 r < b < a,
所以當然把計算簡化了. 接著我們就來看看輾轉相除法. 由於
gcd(a, b) = gcd(- a, b) 所以我們只要考慮 a, b 都是正整數的情況.
r < b < a,
所以當然把計算簡化了. 接著我們就來看看輾轉相除法. 由於
gcd(a, b) = gcd(- a, b) 所以我們只要考慮 a, b 都是正整數的情況.
Theorem 1.3.2 (The Euclidean Algorithm)
假設
a,
b 

且
a >
b. 由除法原理我們知存在
h0,
r0 

使得
a =
bh0 +
r0, 其中
0
 r0
r0 <
b.
若
r0 > 0, 則存在
h1,
r1 

使得
b =
r0h1 +
r1, 其中
0
 r1
r1 <
r0.
若
r1 > 0, 則存在
h2,
r2 

使得
r0 =
r1h2 +
r2, 其中
0
 r2
r2 <
r1.
如此繼續下去直到
rn = 0 為止. 若
n = 0 (即
r0 = 0), 則
gcd(
a,
b) =
b. 若
n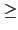
1, 則
gcd(
a,
b) =
rn - 1.
証 明.
首先注意若
r0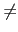
0, 由於
r0 >
r1 >
r2 > ... 是嚴格遞減的, 因為
r0 和 0 之間最多僅能插入
r0 - 1 個正整數, 所以我們知道一定會有
n r0
r0 使得
rn = 0.
若 r0 = 0, 即 a = bh0, 故知 b 為 a 之因數, 得證 b 為 a, b
的最大公因數. 若 r0 > 0, 則由 Lemma 1.3.1 知
gcd(a, b) = gcd(b, r0) = gcd(r0, r1) = ... = gcd(rn - 1, rn) = gcd(rn - 1, 0) = rn - 1.

現在我們來看用輾轉相除法求最大公因數的例子.
Example 1.3.3
我們求
a = 481 和
b = 221 的最大公因數. 首先由除法原理得
481 = 2
. 221 + 39, 知
r0 = 39. 因此再考慮
b = 221 除以
r0 = 39 得
221 = 5
. 39 + 26, 知
r1 = 26. 再以
r0 = 39 除以
r1 = 26 得
39 = 1
. 26 + 13, 知
r2 = 13. 最後因為
r2 = 13 整除
r1 = 26 知
r3 = 0, 故由 Theorem
1.3.2 知
gcd(481, 221) =
r2 = 13.
在利用輾轉相除法求最大公因數時, 大家不必真的求到 rn = 0.
例如在上例中可看出 r0 = 39 和 r1 = 26 的最大公因數是 13, 利用
Lemma 1.3.1 馬上得知
gcd(a, b) = 13.
在上一節 Corollary 1.2.5 告訴我們若
gcd(a, b) = d, 則存在
m, n 
 使得 d = ma + nb. 當時我們沒有提到如何找到此 m, n.
現在我們利用輾轉相除法來介紹一個找到 m, n 的方法. 我們沿用 Theorem
1.3.2 的符號. 首先看 r0 = 0 的情形, 此時
d = gcd(a, b) = b
所以若令 m = 0, n = 1, 則我們有 d = b = ma + nb. 當 r0
使得 d = ma + nb. 當時我們沒有提到如何找到此 m, n.
現在我們利用輾轉相除法來介紹一個找到 m, n 的方法. 我們沿用 Theorem
1.3.2 的符號. 首先看 r0 = 0 的情形, 此時
d = gcd(a, b) = b
所以若令 m = 0, n = 1, 則我們有 d = b = ma + nb. 當 r0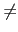 0 但
r1 = 0 時, 我們知
d = gcd(a, b) = r0. 故利用
a = bh0 + r0 知, 若令
m = 1, n = - h0, 則
d = r0 = ma + nb. 同理若 r0
0 但
r1 = 0 時, 我們知
d = gcd(a, b) = r0. 故利用
a = bh0 + r0 知, 若令
m = 1, n = - h0, 則
d = r0 = ma + nb. 同理若 r0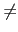 0, r1
0, r1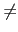 0 但
r2 = 0, 則知
d = gcd(a, b) = r1. 故利用
a = bh0 + r0 以及
b = r0h1 + r1 知
0 但
r2 = 0, 則知
d = gcd(a, b) = r1. 故利用
a = bh0 + r0 以及
b = r0h1 + r1 知
r1 = b - r0h1 = b - (a - bh0)h1 = - h1a + (1 + h0h1)b.
因此若令 m = - h1 且
n = 1 + h0h1, 則
d = r1 = ma + nb. 依照此法, 當
r0, r1 和 r2 皆不為 0 時, 由於
d = gcd(a, b) = rn - 1 故由
rn - 3 = rn - 2hn - 1 + rn - 1 知
d = rn - 3 - hn - 1rn - 2.
利用前面推導方式我們知存在
m1, m2, n1, n2 
 使得
rn - 3 = m1a + n1b 且
rn - 2 = m2a + n2b 故代入得
使得
rn - 3 = m1a + n1b 且
rn - 2 = m2a + n2b 故代入得
d = (m1a + n1b) - hn - 1(m2a + n2b) = (m1 - hn - 1m2)a + (n1 - hn - 1n2)b.
因此若令
m = m1 - hn - 1m2 且
n = n1 - hn - 1n2, 則 d = ma + nb.
上面的說明看似好像當 r0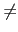 0 時對每一個
i
0 時對每一個
i  {0, 1,..., n - 2}
要先將 ri 寫成
ri = mia + nib, 最後才可將 d = rn - 1 寫成
ma + nb 的形式. 其實這只是論證時的方便, 在實際操作時我們其實是將每個
ri 寫成
mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回 d = ma + nb.
請看以下的例子.
{0, 1,..., n - 2}
要先將 ri 寫成
ri = mia + nib, 最後才可將 d = rn - 1 寫成
ma + nb 的形式. 其實這只是論證時的方便, 在實際操作時我們其實是將每個
ri 寫成
mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回 d = ma + nb.
請看以下的例子.
Example 1.3.4
我們試著利用 Example
1.3.3 所得結果找到
m,
n 

使得
13 = gcd(481, 221) = 481
m + 221
n. 首先我們有
13 =
r2 = 39 - 26 =
r0 -
r1. 而
r1 = 221 - 5
. 39 =
b - 5
r0, 故得
13 =
r0 - (
b - 5
r0) = 6
r0 -
b. 再由
r0 = 481 - 2
. 221 =
a - 2
b, 得知
13 = 6(
a - 2
b) -
b = 6
a - 13
b. 故得
m = 6 且
n = - 13 會滿足
13 = 481
m + 221
n.
要注意這裡找到的 m, n 並不會是唯一滿足 d = ma + nb 的一組解.
雖然上面的推演過程好像會只有一組解,
不過只能說是用上面的方法會得到一組解, 並不能擔保可找到所有的解.
比方說若令 m' = m + b, n' = n - a, 則
m'a + n'b = (m + b)a + (n - a)b = ma + nb = d.
所以 m', n' 也會是另一組解. 所以以後當要探討唯一性時,
若沒有充分的理由千萬不能說由前面的推導過程看出是唯一的就斷言是唯一.
一般的作法是假設你有兩組解,
再利用這兩組解所共同滿足的式子找到兩者之間的關係.
我們看看以下的作法.
Proposition 1.3.5
假設
a,
b 

且
d = gcd(
a,
b). 若
x =
m0,
y =
n0 是
d =
ax +
by
的一組整數解, 則對任意
t 

,
x =
m0 +
bt/
d,
y =
n0 -
at/
d 皆為
d =
ax +
by 的一組整數解, 而且
d =
ax +
by 的所有整數解必為
x =
m0 +
bt/
d,
y =
n0 -
at/
d 其中
t 

這樣的形式.
証 明.
假設
x =
m,
y =
n 是
d =
ax +
by 的一組解. 由於已假設
x =
m0,
y =
n0
也是一組解, 故得
am +
bn =
am0 +
bn0. 也就是說
a(
m -
m0) =
b(
n0 -
n).
由於
d = gcd(
a,
b), 我們可以假設
a =
a'd,
b =
b'd 其中
a',
b' 

且
gcd(
a',
b') = 1 (參見 Corollary
1.2.3). 因此得
a'(
m -
m0) =
b'(
n0 -
n). 利用
b'|
a'(
m -
m0),
gcd(
a',
b') = 1 以及
Proposition
1.2.7(1) 得
b'|
m -
m0. 也就是說存在
t 

使得
m -
m0 =
b't. 故知
m =
m0 +
b't =
m0 +
bt/
d. 將
m =
m0 +
bt/
d 代回
am +
bn =
am0 +
bn0 可得
n =
n0 -
at/
d, 因此得證
d =
ax +
by 的整數解都是
x =
m0 +
bt/
d,
y =
n0 -
at/
d 其中
t 

這樣的形式.
最後我們僅要確認對任意
t 

,
x =
m0 +
bt/
d,
y =
n0 -
at/
d 皆為
d =
ax +
by 的一組整數解. 然而將
x =
m0 +
bt/
d,
y =
n0 -
at/
d 代入
ax +
by
得
a(
m0 +
bt/
d )+
b(
n0 -
at/
d )=
am0 +
bn0 =
d, 故得證本定理.

利用 Proposition 1.3.5 我們就可利用 Example 1.3.4 找到
13 = 481x + 221y 的一組整數解 x = 6, y = - 13 得到
x = 6 + 17t, y = - 13 - 37t
其中
t 
 是
13 = 481x + 221y 所有的整數解.
是
13 = 481x + 221y 所有的整數解.


下一頁: 質數
上一頁: 整數的基本性質
前一頁: 除法原理
Li
2007-06-28
![]()
![]() r < b < a,
所以當然把計算簡化了. 接著我們就來看看輾轉相除法. 由於
gcd(a, b) = gcd(- a, b) 所以我們只要考慮 a, b 都是正整數的情況.
r < b < a,
所以當然把計算簡化了. 接著我們就來看看輾轉相除法. 由於
gcd(a, b) = gcd(- a, b) 所以我們只要考慮 a, b 都是正整數的情況.
![]()
![]() 使得 d = ma + nb. 當時我們沒有提到如何找到此 m, n.
現在我們利用輾轉相除法來介紹一個找到 m, n 的方法. 我們沿用 Theorem
1.3.2 的符號. 首先看 r0 = 0 的情形, 此時
d = gcd(a, b) = b
所以若令 m = 0, n = 1, 則我們有 d = b = ma + nb. 當 r0
使得 d = ma + nb. 當時我們沒有提到如何找到此 m, n.
現在我們利用輾轉相除法來介紹一個找到 m, n 的方法. 我們沿用 Theorem
1.3.2 的符號. 首先看 r0 = 0 的情形, 此時
d = gcd(a, b) = b
所以若令 m = 0, n = 1, 則我們有 d = b = ma + nb. 當 r0![]() 0 但
r1 = 0 時, 我們知
d = gcd(a, b) = r0. 故利用
a = bh0 + r0 知, 若令
m = 1, n = - h0, 則
d = r0 = ma + nb. 同理若 r0
0 但
r1 = 0 時, 我們知
d = gcd(a, b) = r0. 故利用
a = bh0 + r0 知, 若令
m = 1, n = - h0, 則
d = r0 = ma + nb. 同理若 r0![]() 0, r1
0, r1![]() 0 但
r2 = 0, 則知
d = gcd(a, b) = r1. 故利用
a = bh0 + r0 以及
b = r0h1 + r1 知
0 但
r2 = 0, 則知
d = gcd(a, b) = r1. 故利用
a = bh0 + r0 以及
b = r0h1 + r1 知
![]() 0 時對每一個
i
0 時對每一個
i ![]() {0, 1,..., n - 2}
要先將 ri 寫成
ri = mia + nib, 最後才可將 d = rn - 1 寫成
ma + nb 的形式. 其實這只是論證時的方便, 在實際操作時我們其實是將每個
ri 寫成
mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回 d = ma + nb.
請看以下的例子.
{0, 1,..., n - 2}
要先將 ri 寫成
ri = mia + nib, 最後才可將 d = rn - 1 寫成
ma + nb 的形式. 其實這只是論證時的方便, 在實際操作時我們其實是將每個
ri 寫成
mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回 d = ma + nb.
請看以下的例子.
![]()
![]() 是
13 = 481x + 221y 所有的整數解.
是
13 = 481x + 221y 所有的整數解.