
HPM的法國經驗:在教學中融入古代數學問題 11051999
過去這五個學期以來,我的所有課程都在對中學教師演說,這些教師在歷經幾年教學後,又再回到大學來接受外加的訓練。在了解到他們需要一個對日常教學直接有所助益的課程,我便試著去設計這樣的課程;無可避免地,在課程中我必須重複地表達個人對教師日常工作的看法。在我的論點中試圖先假設有一固定的形式,最後,我將它們歸納濃縮成十條規則,或稱『十誡』。
為了清楚說明十誡的意義,本應加上例子,但鑒於空間有限,在此便不再贅述。不過,在我的《數學解題》一書中,舉例說明了一些觀點;而在其他著作中,也可以看到關於此一主題的論述。現在,我將『十誡』列舉如下:
教 師 十 誡
說
明最初,我是針對課堂上的參與者─中學數學教師,來說明前述的十誡。儘管如此,這些規則適用於任何的教學環境、任何層級的任何科目;不過,一般來說,數學教師有較多、較好的的機會去運用它們。現在,我們開始一個一個來考慮,其中將會特別針對數學教師的教學:
以上應足以說明十誡中的第一誡:對你所教授的科目有興趣。
這也應該說明了十誡中的第二誡:瞭解你所教授的科目。
經驗是必需的,實際的經驗使你明白在教室中教師與學生的“教”與“學”,讓你熟悉獲取知識與技能的過程─包括學習、發現、創造、瞭解…等等許多方面。心理學家已經做過很多有關學習過程的實驗並發表了一些有趣的論點。對一位非常善於接納與理解的教師來說,這些實驗與論點具有刺激的作用;但是就我們這裡主要討論的教育方面來說,它們還沒有完善到可以對教師的教學直接有所助益,因此,教師首先必須倚賴個人的經驗與判斷。
根據近半世紀的研究與教學經驗,以及深入內省後,對於課堂教學所需,我在這裡提出一些我認為對課堂教學極為重要的學習歷程的觀點。有一件事是一再地被強調著:主動積極的學習優於被動消極、“僅僅只是接受”的填鴨式學習;愈積極主動便愈好:學習任何一件事的最佳途徑就是親自獨立地去發現其中的奧祕。
事實上,在一個理想的教學計畫中,教師像是一位心靈的“助產士” ─給予學生機會自行去發現亟待學習的事物。而往往因為缺乏時間的關係,此一理想實際上很難達成,但卻可以引領我們通往正確的方向─這就好像沒有人能到達北極星,卻能藉由觀望它而找出正確方向一樣。
於準老師的課程上,上述的十誡簡單明瞭但卻不容易遵循,且我們也沒能夠讓教師們可以易於遵循,例如,教師們的大學學習鮮少能幫助他們去遵循這些誡條。而且,我們在準中學教師的課程上遭遇到一些棘手的問題。我並沒有足夠的時間、空間和方法(或者勇氣)去充分地處理這類問題,然而,有些觀點我卻不得不提出來,這些觀點被在一所北美中學教授代數、幾何、三角學(及少數更高階的科目)的老師們所關心。“一般數學(general mathematics)”或諸如此類多一般性、少數學性的學科並不是我所關切的重點。
我不能忍受在我班級的參與者講出這樣的話:「準老師被數學系及教學法的課程惡劣地對待;數學系講的課我們聽來有如一塊嚼不動的牛肉,而教學法的課卻像一碗沒有肉片的淡湯。」我遇到好幾位教師表達了同樣的意見,但或多或少是覺得害臊的。這些意見的來源到底是什麼呢?
每個人都知道一些例子,比如說教授代數或幾何的老師對這門學科的瞭解程度比學生所追問的還要少;如果我們所談論的講師不是教練或家政老,而是數學教師的話,這種情況就更容易發生了。但不論這類例子是何等異常和普遍的,我可不希望去討論。
有一件事發生地比起如我們所願的還要頻繁:一個能夠勝任和合乎意向的數學教師對中學數學背景瞭解地不夠深,以至於他無法滿足較好的學生的好奇心或知道他們的反應。(有一些觀念應該要,但卻沒有廣泛地被知道:例如無限小數、無理數、可除性、立體幾何的第一個證明…等等)。為何會如此?
大半的準老師們不瞭解或帶著不穩的中學數學知識便離開了學校,而他們應該在何時何地再來學中學數學呢?數學教師修習一些由數學系所提供的相關進階課程,他將會有很大的困難去跟上(或通過)這些課程,因為他的中學數學知識並不充分;他再也沒辦法將這些課程與中學數學相連接。或者他會去修習一些由教育系所提供的有關教學方法的課程,這些課程基本上符合了教育系只教方法而非科目主體的原則。準老師們或許會(幾乎沒有計劃地)接受下面的觀感:教學方法與學科主體的不夠瞭解息息相關。無論如何,他對中學數學的瞭解仍然是最低限度的。
在這裡我要提出一個我覺得更甚於其他的觀點。老師一直被勸告去做很多“漂亮”的事:他該給他的學生不只是資訊而且要讓他們「知道如何做」、鼓勵他們的創意和富創意性的工作,同時讓他們熟知發現的喜悅和張力。然而,教師本身呢?他有機會在他的課程中獨立做數學研究工作嗎?或是有機會獲知他打算傳達給學生的技能嗎?答案是否定的!就我所知,並沒有任何一所大學能給予教師一個還算不錯的機會去發展他在數學方面的技巧訣竅與技能技能。
對於這樣明顯的缺點,我介紹一個補救方法:一個數學教師的『解題討論班』(a seminar in problem-solving),這個討論班所需的知識僅僅只要有中學的水平就可以了,所討論的問題的難度也稍在中學水平之上而已。
如果透過適當引導的話,這樣的討論班可能會有很好的效果。首先,參與者將會有很好的機會透徹地獲知中學的數學知識─真正的、隨時可用的知識,不單單只是記憶而是透過將其應用於有趣的問題之上。然後,參與者可以獲得一些處理中學數學的技巧訣竅、技能及解題要素的洞察力。此外,我也利用討論班讓參與者練習去解釋問題和引導答案;事實上,我也給予他們練習教學的機會,因為他們在平時課堂裡並沒有這樣足夠的機會。經由下列的方式去實施:在某些練習單元的開始,每個參與者會收到一份不同的問題(每個人一題),打算讓他在這個單元解決,但他不能和同事們討論,不過,他可以由引導者給予些許幫助。
在此單元與下一單元之間,每個參與者都應完成、回顧、盡可能地簡化解答並留意其他的解題方式…等等。他也應該為如何在討論班中演示問題與解答詳加計劃一番。關於以上幾點,他有機會可以向引導者請教,然後在下一個練習單元中,所有的參與者組成數個討論小組;每一個討論小組盡量由四位意氣相投的成員組成,其中一位扮演老師的角色,另外三位則充當學生,按法則九及其他誡條,老師對學生演示他的問題,且試著引導他們得到解答。當獲得答案後,接著便會對演示進行一段簡短而友善的評論。然後換下一個成員擔任老師且演示他的問題;這個過程一直反覆進行到每個人都輪過為止。有一些特別有趣的問題或特別好的演示過程稍後會再對整個討論班演示一遍並進行討論。
用討論小組的方式來進行解題相當受到歡迎,而且我覺得整個討論會相當成功。所有的參與者都是有經驗的教師,他們很多人也都感覺他們的參與給他們的班教學帶來了許多有用的點子。
![]()
誠如大家所熟悉,HPM作為國際數學教育委員會(ICMI)的一個研究群,它的組成動機完全出自對於數學的教與學之強烈關懷,因此,它的主要目的在於將數學「教好」或「學好」,而不是讓教師或學生去直接去教或學「數學史」,除非課堂中的「數學史」活動,可以切實地提升數學教育的成效。當然,如果因此導致教師或學生對「數學史」如醉如痴,那麼,她(他)們最終一定可以體會「數學史」乃是數學有機體不可分割的一部份,從而為數學的教與學賦予更深刻的意義。
無論教師與學生如何對待「數學史」,要想在以專業技術知識(technical knowlledge)講授為主的數學教室中,為它尋找一個具有正當性的「位置」,則數學史如何「融入」數學課程(包括教材)及其教學活動之中,顯然是HPM成立二十幾年來所面臨的最重大課題了。
為此,ICMI特別支持贊助HPM編撰ICMI Study Book一書(預定明年出版),以便推動整合HPM的相關學術與教育資源,深化HPM在國際數學教育界中的意義與重要性。(請參考拙文『HPM馬賽行』,見本刊第一卷第二期)現在,謹就我所參與的兩個相關的小組WGA2及WGB2之報告初稿,摘錄一些針對數學史「融入」數學教室的know-how,願與國內數學教育專家及數學教師分享,尤盼大家集思廣益,提出具有本土自主意識的批判觀點與意見。
上述WGA2的主題是『數學史融入數學教室之方式的解析性綜述』(Analytical Survey of Ways of Integrating History of Mathematics in the Classroom),初稿由以色列的Abraham Arcavi與希臘的Costas Tzanakis負責,將我們小組在馬賽討論過的觀點與材料綜合成編,再分送小組成員審定。目前全篇大致底定,其論述基礎是我們共同討論出來的一個架構,底下就針對它,做一些必要的說明。
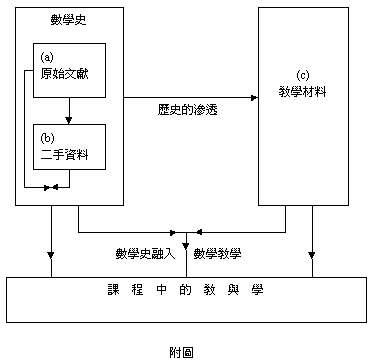
首先,請特別注意此一架構的主體是最底層的「教室中的教與學」(Classroom Teaching / Learning),也就是它的其他支架或成分都是為這主體服務。至於(a)、(b)項所分布的支架,可以說是數學史學範圍的工作(Primary and Secondary Source Materials),而(c)項這個支架,則是我們平常所熟悉的教學材料(Didactic Source Materials),只不過它已經受到數學史的啟發而被「滲透」了(Presentation inspired by History)。這兩個支架的實質內容以及它們的結合,一起匯入底層,共同撐起「教與學」的主體。事實上,教與學的實施結果,也一定反過來回餽(a)與(b)的數學史學支架以及(c)項教學材料支架。譬如,我們常常可以發現孩童的學習特色或困擾,對數學史家的問題意識極具啟發性(請參考拙文「康熙皇帝學符號代數」,載本刊第二卷第一期)。另一方面,教師的實務經驗,當然也一定會敦促教師對教材選擇及教學方式進行反省,蓋「教學相長」故也。現在,讓我們介紹數學史「融入」數學教室的一些 know-how,供有心採用的教師參考:
以上這些 know-how 的例證無法在此細說,不過,我們會陸續利用本刊做比較詳盡的介紹。我們也希望發展更多的例證,來豐富或增添上述 know-how的內容。有志之士,盍興乎來!
![]()
近年來,數學教育已經由從前的重視解題轉變成今日的重視學習過程。順此潮流,國際數學教育界正興起一種新的數學學習方法,那就是所謂的「寫作(writing)」。讀者一定會覺得十分納悶,「寫作」不應該是在國文課或是英文課才會出現的嗎?跟數學有什麼關係呢?其實這裡的「寫作」並不是單指創作文學作品,而是讓學生將自己對數學概念的想法、對解題方法的解釋、對學習數學的感想等等寫成文字,教師批閱,再給予適當的回應,並適時地給予協助。由此可清楚地看出,「寫作」和其他學習方式最大的不同,在於「寫作」不但讓學生反省自己所學的內容,並給予教師許多的回饋,因此師生可以共同創造一種互動的、有生命力的學習環境。
「寫作」對學生學習的幫助可以分成:發展數學知識、發展解題方法、發展自我監控與反思、促進情感表達以及促進討論,下面是扼要列出在這五方面中一些可以充當「寫作」的題材:
一、在發展數學知識方面:
學習是一種複雜的、動態的過程,它與先備知識及將新知識概念化、結合舊有知識體系間的交互作用有關,寫作能提升認知活動的層次,使學習者將修正和重建數學知識的潛能發揮至最大。許多研究者發現「寫作」的確能幫助學生建構數學知識 (Burns,M.,1995; Elliott,W.,1996; Countryman,J.,1992) ,在他們的經驗中,「寫作」與數學成為一股強大的力量,幫助學生理解複雜的概念與系統。此外,「寫作」還有一個額外的功效,那就是學生可以用幽默的方式來表達自己的意見,教師也可以幽默的回應,這對於建立一個良好的學習氣氛有很大的裨益,在這樣的環境中,學生可以更輕易的面對學習中的挑戰。
二、在發展解題方法方面:
讓學生將解題過程,甚至思路過程寫下來,有助於觀念的澄清與認清解題的方向;而讓學生比較、評估不同的解法,或描述在解題的過程中如何使用新學的概念,對於學生的解題能力與分析統整能力都有直接與莫大的幫助。經由此訓練,學生不但可以舉一反三,更可以培養出欣賞數學的能力與態度,此外,教師將會逐漸地發現,學生在思考能力方面會有大幅度的成長,特別是在解應用問題方面的表現。
三、在發展自我監控與反思方面:
自我監控與反思其實就是我們所謂的後設認知行為。後設認知行為與學生有密切的關聯,學生們可以知道並調整自己的思考,這種高層次的認知、處理個人的思考,與在各種學習情境下是否能成功學習有很大的關係,特別是在數學學習與解決問題方面。當學生著手寫下解題時的思路或是解釋理由時,就已經展現了自我監控及反思的行為,如此學生自己就能較明白是哪裡出了問題。更進一步地,教師可以透過寫作評估學生的程度與學習成效,然後給予適當的協助,這比筆試更能正確地掌握學生的學習情況。
四、在促進情感表達方面:
寫作幫助建立一種正面的學習環境,這種環境的目標之一,就是幫助學生獲得在做數學上的自信。許多學生並未被鼓勵去討論學習過程中的挫折、焦慮或無力感,寫作正提供了這樣的宣洩管道,讓學生得以處理在做數學過程中的情緒,如此學生對自己的缺陷與情感經歷,會有一種新的、正確的認知,這讓他們能以一種積極的態度來面對接下來的學習。此外,寫作也可以是一種分享學習喜悅的管道,學生可以經由寫作表達其對學習的愉悅與成就感,而教師更可以抱著分享的心情鼓勵學生,一種良性積極的師生互動於焉而生。
五、在促進討論方面:
寫作可以促進學生與老師間的討論,或是同儕間的討論;討論時需澄清、整理自己的觀念,並用一種對方能夠理解的方式來表達,且在聆聽他人的意見時,也要適時彈性地轉變本身的想法,以利和他人溝通,因此討論可以促使概念間做網狀的溝通聯絡,打破初始時的直線結構。而在整理討論的結果或過程摘要,又再度幫助學生反芻概念間的網狀連結。
結語
透過寫作促進數學學習現已在國際間形成一股風潮,不過國內尚未有相關的研究,其實這種學習法的宗旨概念十分明白清楚,我也相信一定有許多教師在不知不覺中實行了其中的理念,而且獲得了相當大的迴響與回饋。在這裡介紹這種學習法,希望提供給各位老師先進一種選擇,若能經由這樣的學習法創造出適合學生學習的環境,實是台灣教育之福。最後,若有老師有相似的教學經驗或是實施心得,歡迎與大家一起分享!
![]()
台北市景興國中 彭君智老師
三年前,曾以一個很歐幾里德的元宵節參加中小學教師自製教學媒體展,適逢立體教材第一次編入正式課程(補充教材早見於高中數學統合上冊),今年寒假,便找幾個「義工學生」,將校園迴旋梯間閒置已久的溫室,給打扮打扮,順道給數學來點新的風貌。元宵節當天,學校還隆重地舉辦點燈儀式,用鏡面將日光引進龍眼,燈龍點睛,夠炫吧!
說到這三度空間的立體數學(除了立方體常被拿來做代表),從國小、國中到高中,幾乎都只在平面幾何打轉,到了大學,非相關科系的,大概也與之無緣,故透過勞作(製作燈籠)來呈現多面體,期使3D立體更生活化。一套立體做起來,有簡有繁,加上凹凹凸凸及色彩的變化,甚是漂亮。立體燈籠高高掛,彩色模型桌上放,好奇的學生可以低頭研究研究,而一看到數學就頭大的學生,只需抬頭欣賞就好。有興趣,咱們可以做勞作、談數學;沒興趣,只要覺得漂亮,喜歡就好,管他數不數學。數學殿堂之美,讓你不懂數學嘛也通。
當初有這點子,是逛師大夜市時,偶然在拼圖專賣店(註一)瞥到的,買了一組摸索,不小心就推廣到整套立體,當初參展前,還怕侵犯到智慧財產權,特地與專利所有人聯繫,蒙謝大哥看得起當成朋友。有興趣,不妨到其店面欣賞一下(也歡迎來景興走走)。以下簡介製作技巧:拿直尺、量角器量量圖一,相信您可以找出秘訣(註二)。
圖一
【步驟】
用厚紙板裁出上述圖形,稱為n角模
已畫好的三角件 以三角模描輪廓 扇底對齊(3折)
剪下的三角件 三片三角件順時針層疊成正三角形
剪下的紙片稱為n角件,將n片n角件統一順(逆)時針方向層疊,組成一正n邊形,燈籠便如立體拼圖般黏貼完成,特色即為利用n角件不同的層疊量,透過燈光後產生不同的陰影效果,最後配上中國結、流蘇,相信一定讓你愛不釋手。
大學時常聽到一句廣播詞:快樂,就是把看不懂的數學公式,當做外星人寫的詩。每次聽到這句話,總和同學相顧而笑,然後當作我們繼續準備高「危」、「負」變考試的一針強心劑。其實,生活可以很數學,數學也可以很生活。您覺得如何?Don’t worry, just do it.
註一:雷諾瓦拼圖專賣店。紙藝燈籠造型專利:邦興實業
謝榮堯 先生 (02)23629921 北市貴陽街2段216號1F
註二:
三角模 四角模 五角模
三角件組成正三角形,可拼成正四面體、正八面體、正二十面體及各面凸出角錐的星狀多面體;四角件組成正方形,可拼成正六面體及各面凸出角柱的柱狀多面體;五角件組成正五邊形,可拼成正十二面體;若將各種角件搭配(設計及製作方式稍有不同),可拼成阿基米德半正多面體。
![]()
科 展 二 三 事
台北市景興國中 彭君智老師國三時頭一次聽到科展,三位同學被「派」去研究,後來一位保送武陵。高一時,和同學做水果電池(每班要出一件作品),結論是:誰來發明「四用電表」?教書之後,指導過兩次科展,很幸運的有點成績,在此拋磚引玉,把些許見聞和心得與大家分享:
【現況】:科展在各縣市早行之久遠,但在專事「傳道、授業、解惑」的學校,則如天高皇帝遠;而在某些學校則是「皇上不急,急死太監」,被列為資優班師生的重點項目。故每年一度的盛會,似乎成了「科展老兵」的聚會。
【指導】:一般說來,科展難,難在沒有題目、沒有課本、沒有人教,而最為人所詬病的便是:老師捉刀。其實「教與學,本相長」,指導教師絕對會變成「共同研究者」。學生查資料、整理、研究、下結論,但通常不完整(畢竟所知、見聞有限),指導老師便會技癢難耐地「下海」協助,從引導、拓展到歸納,甚至做到後來比學生還認真(知之、好之、樂之)。至於全由老師做好「教」給學生的情形,只能說是少了「教師組科展」,埋沒了有志之士。然而校內科展通常相反,老師真的只掛名、沒指導(鼓勵報名之後,便是修行看個人),學生甚至也沒請教過師長,以致有的研究產生偏差、選錯數據;有的想法很好,但走不下去。如今年本校很多組做商高定理,其中一組曾想過三次方的推廣,但不了了之,若能適時點出費瑪最後定理這段歷史,相信「驚喜」便是學生此次科展的最大收穫。
【評審】:第一年北市評完,學生笑不出來,因為教授只對隔壁的電腦有興趣;全國時,學生快哭出來,因為教授愛問不問的。今年可能是位置佳,教授有興趣,問了近二十分鐘,學生出來信心滿滿;全國時則完全相反,教授進門,劈頭就罵,只見有些學生被罵得一蹋糊塗,還來不及說重點,教授已走人;有的雖有招架之力,但也信心全無;只有幾組幸免於難,甚而請到辦公室複審。姑且不論教授對作品的關切程度與得獎是否成正比,但是以「不聞不問」,或是像「審論文」般的態度來對待中學生,似乎不甚恰當。不論是否會得獎,作品好的地方就該鼓勵,若有不完整或是錯的地方,點出來,讓學生了解、改善;萬一真有書籍、刊物與作品雷同,更是提出資訊供學生參考、比較的好時機,因為就數學歷史而言,這種「家常便飯」,鼓勵都嫌來不及(除非是存心抄襲)。而學生提出來的疑問,也應盡量深入淺出的給予回答(對象只是個中學生),而不是群、拓樸等專有名詞。至於罵,相信是最失敗的身教與言教。
數學上的家常便飯(不同的人、時、地、事、物,竟發展出相同的定理),只要懂得珍惜,都可以是山珍海味,舉個例:提到畢氏定理,相信不少老師會介紹些歷史:百牛定理、根號2跳海、勾股弦圖¼ 等,甚至費瑪也參一腳。以下這個畢氏的發現請大家玩味:如何從圖形數(註一)推論出弦、股數差1的直角三角形?例如(勾,股,弦)=(3 , 4 , 5 )、( 5 , 12 , 13 )、( 7 , 24 , 25 ) 不少學生(通常不是考一百的)由觀察、類比,很快就推算出接下來會是( 9 , 40 , 41 )、( 11 , 60 , 61 )¼ (註二),奇怪的是,對圖形數卻都沒輒。每當下課前點出答案,學生才發現「被耍得漂亮」,不要說弦、股數差1,要找差n的也不是問題(註三)。
課堂上,大家習慣用「結果論」:告訴你三角形內角和等於一百八十度,然後才去用各種作圖、摺紙、剪貼等方式說明為什麼?補習班最強,直接印一疊比課本還厚的「攻略本」,如此能出幾個像巴斯卡的怪胎:重新發現三角形內角和定理?而身為數學教師的我們,對於數學,又曾有過多少像阿基米德發現浮力原理般的驚喜?其實,不論是對老師還是對學生而言,數學處處都可以是科展(不是每個都要拿去比賽),只要細細品嚐,哪天不小心,你我就可能踩著前人走過的足跡,再次享受發現的樂趣,甚而打開數學å 的另一片天。
註一:圖形數詳見數學家傳奇(九章出版社p.98~p.100)
註二:學生通常可觀察出下列結果,再經定理計算確認。
a:勾為連續奇數 (3,5,7,9,11¼ 等差數列)
b:股為二階等差數列 (4,12,24,40,60¼ )
c:勾的平方= 股+ 弦 (還有不少漂亮的結果)
p.s.還未曾碰過能由題意推算出公式的學生:
註三:畢氏學派的發現,其來有自:萬物皆為數(而且是有理數),故當發現驚為「神喻」的定理時,當然得和教義相輔相成,否則就得去跳海—發現無理數,而找出所有整數邊的直角三角形,就等於是找出所有有理數的直角三角形。圖形數在這裡扮演了重要的角色:
三角數(Ti=1,3,6,10,15¼ )其實就是等差級數數列
四角數(Ri=1,4,9,16,25¼ )碰到平方,故線索就在其中。它可以表示成兩個連續三角數的和:Rn = Tn + Tn-1,或是首n個正奇數的和:
Rn = 1 + 3 + 5 +¼ + ( 2n-1),觀察 3*3= 1+2+3+2+1 =1+3+54*4= 1+2+3+4+3+2+1 =1+3+5+7 5*5=1+2+3+4+5+4+3+2+1=1+3+5+7+9
到底弦、股數差1的關鍵在哪?(可別想得太複雜,免得事後發現被耍)原來5*5 =1+3+5+7+9 = 4*4+9,所以從Rn到Rn+1所加的奇數2n+1,若恰為四角數時,即為所求,而且很快就能歸納出註二中一籮筐的現象。欲求弦、股數差n時,只要從Ri到Ri+n所加的(2i+1)+(2i+3)+¼ +(2n-1)恰為完全平方數時,便萬事OK,也能找出註二般一卡車的結果。從時代背景來看這樣有目的的發現,您說美不美?
『數學教師專業發展』之研究的他山之石
台師大數學系 洪萬生教授俗話說:『名師出高徒!』所以,數學學得好的名師,數學當然教得呱呱叫!不過,這樣的『說法』現在看來,可能只說對了一半,因為它的『脈絡』有問題,大家可能都忽略了一個事實:即使是菁英教育的環境,從教師的『自我學習』到『教導他人學習』之間,仍然經常出現極難跨過的鴻溝!癥結之所在,或許是我們始終不把教師與學生各自的智識發展(intellectual development)之間的連結,當作促進『教師專業發展』的首要任務。現在,請讓我們一起學習如何去面對吧。
本文是一篇中文摘要,也不小心地摻雜了筆者自己的一點心得,請讀者不吝指教。原文是Thomas Cooney所寫的 “Considering the Paradoxes, Perils, and Purposes of Conceptualizing Teacher Development”,預定提交『1999年數學教師教育就學術研討會』(五月10-14日,台灣師大數學系)。教師(專業)發展的概念化是本文的重點。它主要研究『教師改變』(teacher change)-- 從遵循成規的靜態世界到奉探索與反思為圭臬的(動態)世界的個人的智識歷程。至於內容則涉及知識論(epistemology),道德哲學(moral philosophy)以及數學教師的培育與專業發展(teacher professional development),份量頗重,值得精讀。
本文第一節的主題是『教師改變及其道德蘊含』(The notion of teacher change and its moral implications)。作者Cooney首先引述杜威所主張的教育之目的 – 提供手段或工具讓受教者可以最佳方式控制自己的命運。為此,杜威認為受教者必須學習如何通過反思活動(reflective activity)去重新建構或組織過去的(學習)經驗,以便賦予意義,同時也強化往後(學習)經驗之主導能力。因而,教育的功利觀點過分窄化它的價值,不符合民主社會的要求。既然如此,對杜威而言,教育顯然有了道德意涵,亦即它混合了知識(knowledge,實然)與行動(conduct,應然),而且前者對後者提供了『知會』之功能。
Ball and Wilson (1996) 呼應了杜威的觀點,他們認為:在教學上,智識層面與道德層面往往是不可分割的。如果數學無關道德,何以它的教學涉及道德?其答案不僅在於知識內容本身,也與吾人如何獲得這些知識內容有關。譬如教師有責任提供學生機會去把握那些需要論證與澄清的概念。一旦學生的論證過程導致錯謬的結論時,那麼,傾向結果導向教學(product orientation toward teaching)的教師,就會面臨是否讚許此一論證過程的道德兩難。然而,以建構主義(constructivism)為教學導向的教師,對這樣一位學生的學習,一定會賦予完全不同的評量。顯然,此一評量差異取決於信仰(belief)的不同,連帶地所依賴的證據(evidence)也就莫衷一是了。
這種信仰的取捨,當然也影響『優良教學的概念』(the notion of good teaching)。是的,如果所謂的『優良教學』是勤勉講解(telling)與諄諄善誘(caring),那麼,『結果導向教學』就成為最自然的選擇了。在這種情況下,關於教師角色的比喻,職前教師大都選擇『教練』、『園丁』以及『諧星』,因而『師資培育的道德維度』(moral dimension of teacher education)的相關問題,譬如,師資培育課程究竟如何實施?我們打算培育什麼樣的教師?當然都關聯到培育者所採取的立場了。
在本文第二節中,作者評介五篇關於『教師改變』(teacher change)的研究論文(以Journal of Mathematics Teacher Education刊載的論文為主),分別是 (1) Wilson and Goldenberg (1998);(2) Grant, Hiebert and Wearne (1998);(3) Schifter (1998);(4) Jaworski (1998),以及(5) Frykholm (1999)。Wilson與Goldenburg針對一位已經有21年經驗的中學教師教學改革進行研究,結果發現成效極其有限。Grant等人研究十二位企圖改革教學的小學教師,結論是『教師改變』的過程,正如同他(她)們對數學及其教學的信仰一樣複雜。Shifter探索兩位中學教師對數學的瞭解與數學教學的關聯,證明教師專業發展(的成效)可以轉化進去實際教學之中。Jaworski針對教師的教學提供了一個行動研究(action research),結果發現參與研究的教師在反思活動的循環中(cycles of reflective activity),對數學及其教學的觀點與實踐,有了很大的改變。Frykholm考察了63位中學教師對NCTM 標準(Standards)的反應,這些職前教師在三年間接受了以此為基礎的師資培育改革課程,不過,她(他)們很少注意到這些標準只是某種教育哲學的再現,對於這些標準與實際教學的脫節,也甚表困惑,因此,Frykholm建議我們應該鼓勵職前教師檢視她(他)們的信仰與教學決策之間的矛盾。
Cooney將上述所有這些研究結果,拿來對比Guskey的『教師改變』模型,可是他無法確定:對教師而言,究竟是信仰(beliefs)還是實際教學(practice)改變在先?他認為這畢竟不全是一個取決於證據的經驗問題,因為教師關於數學及其教學的信仰,顯然決定了何者可視為證據。如此一來,信仰如何被建構也因此變成了必須被正視的問題了。
於是,在本文第三節中,Cooney針對「教師改變」的一個理論性觀點(a theoretical perspective for teacher change)提出討論。他指出:關於信仰是如何被建構的研究文獻並不多見。在本節中,作者首先說明「知曉」(knowing)與「相信」(believing)的差異,並引述Scheffler (1965) 對信仰所下的定義。接著,介紹 Green (1971) 對信仰的建構所做的形上學分析,以便回答「信仰可以改變」是怎麼回事。在這個關聯下,Cooney 特別指出吾人信仰中都有兩個關鍵的成分,亦即懷疑(doubt)與證據(evidence)。
基於此,如果我們認為信仰的改變應該先於實際教學的改變,那麼,師資培育者理應考慮哪些經驗可以充當改變的證據。另一方面,如果認為教師信仰之改變必須由可以察覺的學生之學習表現來證明,那麼,問題就變成哪一類證據可以解釋學生的更佳表現。無論採取哪一種立場,「懷疑」這個概念都十足重要。即使在前述Guskey的模型中,信仰的改變都必須伴隨著對現行教學方式之懷疑。
既然吾人承認『改變』繫乎『懷疑』,那麼,考慮各種介入個人懷疑之意願的方案(scheme),就變得很有意義了。於是,Cooney依次引述Perry (1970, 1990)及Belenky, Clinchy, Goldberger, and Tarule (1986) 關於個人智識發展階段(stages of intellectual development)的研究,指出進階(的可能性)來自於個人有意願以在脈絡的方式觀察情境(willingness to see situations contextually),因為『在脈絡』(contextuality)孕育懷疑,而後者正是改變的條件。
以上述Perry與Belenky等人的論述為基礎,Cooney也引述了Baxter Magolda (1992) 的研究成果。Baxter Magolda研究101位男女大學生在大學四年間的智識發展,歸納出四個互異的思維階段:絕對性的知曉(absolute knowing),過渡性的知曉(transitional knowing),獨立性的知曉(independent knowing),以及在脈絡性的知曉(contextual knowing)。其中比較本質的變遷出現在第三個階段,亦即『獨立性的知曉』,此時的個人,不同於前兩個階段時的動輒訴諸權威,而認定知識大都是不確定的(most uncertain)。至於Baxter Magolda所謂的『在脈絡性的知曉』,是指所有知識所以不確定,全都是在脈絡中被定義(contextually defined)的緣故。她也發現研究對象中,只有57%到畢業時達到第三個階段,至於達到第四階段者,則只有12%!
基於類似的考慮,King and Kitchener (1994) 注意到個人智識發展過程中,反省的傾向極為關鍵,因此,他們發展出針對反省的思維發展模型,其中分成三個層次,即前反省的思維(pre-reflective thinking),準反省的思維(quasi-reflective thinking),以及反省的思維(reflective thinking)。這最後一個思維層次,是指知識是以在脈絡的方式被理解,而且其相關證據也不斷地被重新檢驗與評估。King and Kitchener發現反省的思維模式最可能出現在大四學生身上,至於其它的學生,則多半以前兩個層次的思維為主。
所以,研究數學教師的信仰,絕對不能忽略上兩段的結論。為此,Cooney, Shealy, and Arvld (1998a) 特別提供了一個刻劃數學教師信仰的概念架構,其中描述了四種立場:即孤立論者(islationist),素樸的理念論者(naive idealist),素樸的關聯論者(naive connectionist),以及反省的關聯論者(reflective connectionist)。粗略地說,這四種立場都是針對教師如何處理教材內容(content)與教學方法(pedagogy),不只反映出數學教師抗拒或調適新教學法進入他(她)們的教學方案之中,同時也展現了教師對數學及其教學的反省導向。當然,擁有不同立場的數學教師,也在他(她)們對數學及其教學的信仰是否可以改變,表現了相應的特色。當然,反省的關聯論者被認為是能夠在脈絡中反省教學活動或策略的數學教師。因此,我們必須幫助教師瞭解教學活動或策略本身無所謂好壞,要緊的是他(她)們必須體認是『脈絡』決定了有效與否。
上述這些關於智識發展的方案,都指出了決定個人如何有知的多種方式中所涉及的認識論議題。誠如Hofer and Pintrich (1997) 所說的,檢視這些論述,『將有助於我們瞭解關於學生與教師對知識與對知識的思維之信仰。從而這一資訊,也可以幫助我們更好地瞭解教室中的教學與學習過程。』因此,這些方案的確可以作為研究教師專業發展的概念性架構。
在本文第四節中,Cooney利用五個教學上的解題(pedagogical problem-solving)之例子說明Hofer and Pintrich的觀點。根據他自己三十多年培育中學準教師的經驗,Cooney發現:檢視學校數學(school mathematics),是研究教師對數學及其教學的信仰系統之最佳切入點。這是因為在此,相對於數學及教學法而言,『懷疑』很容易出現。所以,Cooney認為教材內容與教學方法如何(『在脈絡地』)整合(integration of content and pedagogy),可以測試準教師的反省思維能力。而這正是他設計這五個例題的主要考慮。這也就是說,這些題目被呈現的『脈絡』,完全是基於讓教師有機會重新反省他(她)們對數學及其教學的信仰之考慮,同時也鼓勵他(她)們有機會發展自己的數學教學之哲學。
根據本文的論述,準教師對數學及其教學的信仰顯然大大地『乖違』我們的改革導向之師資培育課程,其中所顯現的弔詭與險阨,也很容易察覺與辨識,尤其是把它們放置在本文所提供的理論性觀點下,更可以深入地分析。至於本文討論智識發展方案與模型的主要目的,則在於一方面,教師可以利用它們作為學童教育的基礎,而在另一方面,則是我們師資培育者,也可以利用這些模型去將教師如何對世界賦予意義加以概念化,如此一來,我們的培育工作就會擁有方向與目的。再者,正如我們希望教師以一種『科學的』方式 -- 亦即依據他(她)對學生知識背景的瞭解 – 進行教學,我們對教師的教學,也應該奠基於對他(她)們的世界之實用性詮釋。而這也正是我們目前亟需的師資培育的科學(the science of teacher education)!