首次分科數甲考題，除了極少數人認為有超綱的題目（這一點後面會談），基本上沒有太大的問題。除了有些題目答對率出奇的低外，從選項分析來看也只有第8題(極限那一題）有選錯誤選項的比率異常高於選正確選項的情況發生外，其他還算正常。所以我僅挑幾題，認為一些概念對學生應該有幫助的來談。我有參與此次數甲考試閱卷工作，答題的狀況非常的差。可能和今年數A一樣，學生看不懂題目。只是數A是看不懂中文，數甲是看不懂數學。閱卷發現，考生對微積分的熟悉度，遠遜於過往幾年。這應該不是課綱的問題，可能是申請學校制度、時程的改變，不利於學生學習高三的數學，更不利於那些申請學校不順利後，想考好數甲的考生。也可能今年數A較難，數學好的同學都能以好的數A成績申請到好的學校，今年數甲的閱卷，已不復見以往有些令人驚艷的答題狀況出現。以下是對份試卷幾個題目的分析：
這應該是多選題題型中考生最愛的，只要做一次就可將答案選出，而不像其他的多選題好像做五個是非題。不過此題得分率竟然不到$60\%$，以大考中心的標準為中偏易，而不是易。關於本題的得分率與鑑別度，大考中心提供的分組資料如下（對各項目的說明，請參考111數A第一題的說明；有關於多選題得分率的說明請參考111數A第9題的說明）：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | 87 | 28 | 92 | 79 | 61 | 41 | 22 | 46 | 59 | 13 | 18 | 20 | 19 |
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60 | 82 | 37 | 87 | 74 | 61 | 48 | 31 | 39 | 45 | 13 | 13 | 13 | 17 |
好了！讓我們回到原來的題目。會特別挑這個題目出來談，覺得這樣的題目學生拿不到分數真的很可惜。這是屬於操作型的題目，應該鼓勵學生試看看。不過看到許多老師一開始就列出式子 $x^3+2x^2-2x+k=(x^2+ax+1)(x+k)$. 為什麼是乘上 $x+k$ 呢？108課綱已不太強調根與係數問題，學生可能無法直覺想到乘上$x+k$. 他們應該知道乘上一個一次式 $cx+d$. 不過這樣又太多未知數，會不會是這樣讓他們不敢做下去呢？即使勇敢做下去，下一步便是要面對解比較係數後的方程組：$\left\{\begin{array}{rrl}k & +a &=2 \\ ka&+1&=-2 \end{array}\right.$ 會不會是這個方程組不會解呢？這都是我們需要了解並加強的。這類問題可考慮避開比較係數，鼓勵學生用長除法處理，即 \[\begin{array}{r} 1\,\quad\phantom{(k+}2-a \\ 1\qquad a\qquad 1\,\,\overline{\smash{\big)}\,1\quad\phantom{a-}2\quad\phantom{a^2-a}-2\,\quad\phantom{(+a-2}k}\\ \underline{1\quad\phantom{2-}a\quad\phantom{a^2-2a-}1\quad\phantom{k+a-2}}\\ 2-a\quad\phantom{a^2-a}-3\,\,\,\quad\phantom{+a-2}k\\ \underline{2-a\quad\phantom{(3-}2a-a^2\quad\phantom{k+}2-a}\\ a^2-2a-3\quad k+a-2 \end{array}\] 這個方法，只要會符號操作學生應該沒問題。而且會發現不會牽涉到解方程組，只要餘式的一次項為 $0$ 就可以解出 $a$ 來，且也可因此馬上得到商式，根本不需解 $k$. 我們也可以嘗試將問題改為：已知 $f(x)$ 除以 $g(x)$ 的餘式為常數多項式，且 $g(x)=0$ 有實根，求 $f(x)$ 除以 $g(x)$ 的商式為何。讓學生體會長除法，與比較係數的差異。
本題除了得分率偏低（$43\%$, 屬中偏難），以及錯誤的選項(5)在低分組中被圈選的比率異常的高外，沒有什麼特別詭異的。低分組考生大部分會圈選選項(5)的原因，可能是代了一些第一象限的點就誤以為它是對的，這當然還是得多糾正學生，若要代點需考慮各種不同情況，以及用代的若發現錯便能確認選項錯誤，但未發現錯並不代表選項正確。 事實上由本題前三個選項確認是一個旋轉加伸縮的映射後，後兩個選項就可以用圖形看出了。所以想藉這一題談一談何時可用圖形看出，何時不宜（看來我仍對今年數B第8題(打靶那一題)吃癟仍耿耿於懷）。
這一題由前三個選項確定是旋轉$30^\circ$，再伸長$2\sqrt{3}$，後兩個選項只是問圖形相關位置，所以可以完全由圖形看出。即使旋轉角度，伸縮長度算錯，也能處理，所以完全是觀念的問題。我們可以考慮 $C,O,C'$ 所形成的兩邊長 $\overline{OC},\overline{OC'}$ 分別為 $1,2\sqrt{3}$ 且夾角 $\angle C'OC$ 為 $30^\circ$ 的三角板。當移動$C$點時要了解$C'$如何變化，此時可以用將頂點$O$固定的方式來擺放此三角板。所以選項(4)就是問有沒有可能找到擺放方式使得三角板的邊$\overline{CC'}$與$x$-軸平行。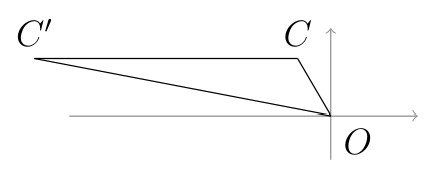
是不是很簡單啊！至於選項(5), 學生就必須先了解 $x$-軸坐標小於 $y$-軸坐標的點表示在直線$y=x$上方的點。因此就可以將選項(5)改成是否有可能找到擺放方式讓三角板的$C$點在$y=x$的上方，而$C'$在$y=x$的下方。
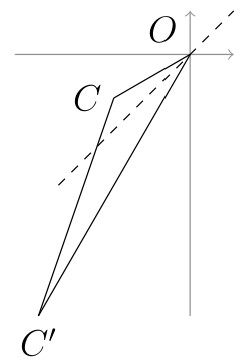以後遇到這類旋轉的問題，都可以鼓勵學生嘗試用這種三角板的看法處理。例如這裡，我們就可馬上知道$C$和$C'$的距離是固定的(學生也可順便練習用餘弦定理算出距離)。看到有些老師選項(4)直接坐標操作，得到滿足題設的直線方程。這不錯，能讓學生了解這條直線上的點經由變換後其$y$坐標不變（同學也可以用三角板等比率伸縮看出這一點）。也有些老師選項(5)直接找到反例的點，說明它是錯的，就比較沒必要了。想想數B第8題都能說用圖形看出了，這一個更可以這樣說。其實還是得說一下，數B那一題能否用圖形看出，關係著圖形的精準度以及每個人對“明不明顯”的看法有差異，最好還是驗證比較好；而這個選項與精準度無關，當然可以用圖形說明即可。
同場加映：對於程度較好的同學，這類旋轉的問題可以讓他們用極坐標，極式處理看看，順便練習以下和角公式。甚至也可和複數連結。例如此題若考慮在高斯平面上$C$點所對應的複數為$z$, 若令 $w=2\sqrt{3}(\cos30^\circ+i\sin30^\circ)=3+\sqrt{3}i$, 則 $C'$ 就對應到 $wz=(3+\sqrt{3}i)z$. 選項(4) $C$ 和 $C'$ 的$y$坐標相同，就表示 $(3+\sqrt{3}i)z-z$ 的虛部為 $0$, 也就是說 $(3+\sqrt{3}i)z-z$ 為一個實數$r$, 即 $(2+\sqrt{3}i)z=r$, 得 $\displaystyle z=\frac{r}{2+\sqrt{3}i}=\frac{r}{7}(2-\sqrt{3}i).$ 另一方面複數 $z$ 的實部是 $\displaystyle \frac{1}{2}(z+\overline{z})$, 虛部為 $\displaystyle \frac{i}{2}(\overline{z}-z)$, 所以選項(5) $z$ 的實部小於虛部就是說 $z+\overline{z}< i(\overline{z}-z)$. 由這能否推導出 $wz+\overline{wz}< i(\overline{wz}-wz)$ 呢？注意複數無法比較大小，前面兩個不等式因為都是實數所以有意義，但複數並無實數不等式的運算性質。例如：$a,b$ 是實數 $z$是虛數，不能由 $a< b$ 而說 $a+z< b+z$. 所以選項(5)應該不成立。我們當然不能用這理由說選項(5)是錯的，這裡只是想提醒複數無法如實數一樣處理不等式。
這一題，評量一個簡單但學生可能缺乏的極限概念。剛看題目覺得是很不錯的題目，但仔細深思，極限觀念未成熟的人可能無法體會這個題目在評量什麼。果不其然，全國考生的得分率僅$19\%$（略微高於另兩題選填題，但那兩題幾乎沒有猜答的機會）。而成績在前$20\%$的考生，此題的得分率也僅$28\%$, 遠低於剛才所提的那兩題選填題的答對率 $36\%$ 和 $53\%$. 可見這一題得分率會比那兩題高，還是靠低分組猜答拉拔起來的呢。此題五個選項全對的僅佔全部考生的$4\%$, 各個分組的鑑別度更低到是個位數。一個好題目，卻變成一點評量價值都沒有的爛題目，最後僅剩下“教育意義”了。希望老師們能珍惜這一題最後的價值，利用它好好教導學生正確的極限概念。以下是它的答對率與鑑別度：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 19 | 25 | 14 | 28 | 20 | 17 | 16 | 12 | 4 | 11 | 8 | 3 | 1 | 4 |
仔細看看選項分析就會知道沒錯，錯誤的選項(1)(4)被圈選的比例都高於正確的選項(2)(5)。很明顯的，這顯示考生極限的概念有明顯的偏差。以下是大考中心提供的本題選項分析資料（對各項目的說明，請參考111數A第一題的說明）：
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | 64 | *58 | 30 | 64 | *48 |
| H | 1 | 61 | 71 | 18 | 60 | 43 |
| L | 1 | 63 | 48 | 47 | 66 | 51 |
到底這題是評量什麼極限概念呢？應該從極限的定義說起。我們就拿題設的 $\displaystyle \lim_{n\to\infty}a_n=6$ 來說吧！老師一般可能說得很籠統，我聽過幾個的說法。一種是：當$n$越來越大時, $a_n$越來越靠近$6$. 這個說法不好，學生會誤解需越來越靠近，事實上有可能是以靠近一點後又遠離一些這樣的模式逼近。另一種說法是：當 $n$ 很大時, $a_n$ 會很靠近(有的會說任意靠近) $6$. 這個說法也不好，因為學生不知道這裡“很大”到底是多大，“很近”到底是多靠近。曾經在數A的題目中發現，學生以為$100$就很大了（111數A第10題）；差了$0.05$就以為很靠近（111數A第9題）。還是嘗試用精準一點的說法：隨便找一個包含$6$的開區間, $a_n$ 會在某一項之後全部都落在此開區間之內。這裡的某一項，沒有要求要多大，只要有就好。 從這個看法，我們來看看選項(4),(5)問的是 $a_{10000}$ 是否會掉入 $(5.9,6.1)$ 這個包含$6$的開區間。若僅由 $\displaystyle \lim_{n\to\infty}a_n=6$ 這個假設，我們僅知 $a_n$ 會在某一項（或許是第一百萬項之後）全部掉入這個區間，所以未必會在第$10000$項發生。了解極限定義的學生，在 $a_n$ 沒有其他的條件限制下，應該不會有衝動選(4),(5)兩個選項。了解極限定後，學生應不難理解以下的重要結論：一個收斂（極限存在）數列，若將其中有限項任意更動，所得的數列依然有相同的極限。例如考慮每一項都是$6$（即 $a_n=6$）的數列$\langle a_n\rangle$, 將其前$10000$項任意換成其他的數字，所得的數列其極限依然是$6$ (這也再次說明選項(4)(5)一般來說是不正確的）。
好，讓我們就用這個概念處理這一題。首先選項(1)很明顯的是將 $a_n$ 都認為是 $6$ 來處理，但我們已知$\langle a_n\rangle$前面幾項，隨便更換成其他的數字，只要符合題設的不等式，所得的數列極限依然是$6$, 因此這個選項應該不正確。 事實上我們只要更改 $a_1$, $b_1$ 使其符合不等式 $b_1+3< a_1< 3b_1$但不符合選項(1)即 $b_1<6-3=3$, 就可以了。因為此時僅更動 $a_1,b_1$, 其他項都不改變的新的數列 $\langle a_n\rangle$, $\langle b_n\rangle$, 仍符合題設，所以就找到選項(1)不正確的反例了。要找反例，我們可以考慮 $b_1=4$（因為要不符合 $b_1< 3$）然後選 $a_1$ 介於 $b_1+3=7$ 和 $3b_1=12$ 即可（例如$a_1=8$），故選項(1)是錯誤的。前面說過選項(4)(5)很可能也是錯的，所以我們希望藉由剛才的想法，更動 $a_n,b_n$ 的前 $10000$ 項，看看能否得到反例。要找到 $a_n,b_n$ 符合題設的不等式 $\displaystyle b_n+\frac{4n-1}{n}< a_n < 3b_n$, 我們發現 $b_n$ 必需滿足 $\displaystyle b_n+\frac{4n-1}{n} < 3b_n$, 這樣才有可能將 $a_n$ 擺在它們之間。換言之，要存在符合題設的不等式的 $a_n,b_n$，那麼 $b_n$ 需符合 $\displaystyle b_n>\frac{4n-1}{2n}$, 所以選項 (2) 是對的。剛剛我們選的 $b_1=4$ 對所有 $n$ 皆符合 $\displaystyle 4>\frac{4n-1}{2n}$, 所以我們可以考慮 $b_1$到 $b_{10000}$ 皆為 $4$（其實大於$2$的數都可以，我懶得換）, 此時對於所有從 $1$ 到 $10000$ 的整數 $n$, 我們只要找 $a_n$, 介於 $\displaystyle b_n+\frac{4n-1}{n}=4+4-\frac{1}{n}$ 與 $3b_n=3\times4=12$ 即可。所以我們考慮 $a_1$到 $a_{10000}$ 皆為 $8$. 也就是說當我們將原數列 $\langle a_n\rangle$, $\langle b_n\rangle$ 的 $a_1,\dots,a_{10000}$ 都用 $8$ 取代，而 $b_1,\dots,b_{10000}$ 都用 $4$ 取代。此時新的兩數列依然滿足題設，但 $a_{10000}=8>6.1$ 故選項 (4) 錯誤。選項(5)呢？為了想找到反例 ($a_{10000}\le 5.9$), 而 $a_n$ 又受限於 $b_n$, 所以我們找的 $b_n$ 應該儘量小。但選項(2)告訴我們 $\displaystyle b_n>\frac{4n-1}{2n}$, 它小不下來。也就是 $a_n$ 既然要大於 $\displaystyle b_n+\frac{4n-1}{n}$, 它一定得大於 $\displaystyle \frac{4n-1}{2n}+\frac{4n-1}{n}=6-\frac{3}{2n}.$ 因此 $\displaystyle a_{10000}>6-\frac{3}{20000},$ 選項(5)成立。從這個角度來看，若了解極限的學生，應該知道選項 (1),(2),(4),(5)根本與 $\displaystyle \lim_{n\to\infty}a_n=6$ 無關，只是問不等式的問題。不過選項(3)問的是極限，所以和前面調整有限項的概念不同，必需全部一起考量才能回答符合題設的數列 $\langle b_n\rangle$ 是否收斂。 選項中似乎暗示著 $b_n$ 也可被兩數列夾住，事實上我們有 $\displaystyle \frac{4n-1}{2n}< b_n < a_n-\frac{4n-1}{n}$ (或 $\displaystyle \frac{1}{3}a_n< b_n < a_n-\frac{4n-1}{n}$)。由於兩邊夾住 $b_n$ 的數列其極限都是$2$, 所以由夾擠定理可得 $\langle b_n\rangle$收斂到 $2$.
老師請注意：看到許多老師在講解選項(1)(4)錯誤時，很認真的去找反例而且舉的反例都是用 $n$ 的形式表示的數列。例如 $\displaystyle a_n=6+\frac{2000}{n}, b_n=2+\frac{2000}{n}.$ 建議不要用這個方式解說此題。要知道，要找到收斂級數就不容易了，還要滿足不等式且不符合選項，對學生來說這是難上加難，根本不可能在考場上想得出來。可以理解這應不是這一題的重點。或許學生也都是這樣的想法，才造成如此低的得分率。另外，這也會誤導學生以為所有的數列都要用 $n$ 的形式表示，這樣就更難體會收斂數列隨意更動有限項仍不會改變其極值的意義了。或許有些老師會覺得我前面解說中舉的例子根本就不能算反例，因為沒有真正“看到”這兩個數列。其實整個邏輯是這樣的，題目給了數列$\langle a_n\rangle$, $\langle b_n\rangle$, 符合假設，然後問選項(1),(4)是否正確。當然了一開始給的數列我們無法確定選項(1),(4)是否正確，但我們的做法就是不管怎樣都可更動原來數列的前幾項使得它仍符合題設，但不符合選項(1),(4). 或許有人會疑問，那原本就沒有符合題設的數列$\langle a_n\rangle$, $\langle b_n\rangle$ 怎麼辦？哈！這點，我想出題者應該會小心注意有這樣的數列存在的，否則大考中心就得送分了。為了清楚說明這個想法、或許老師可以舉例，例如對任意正整數 $n$ 令 $\displaystyle a_n=6-\frac{1}{2n},b_n=2$. 這兩個數列$\langle a_n\rangle$, $\langle b_n\rangle$符合題設也符合選項 (1),(4), 然後問學生如何更動這兩個數列，使它們仍符合題設但不符合選項(1),(4). 這樣會比剛才所說直接給兩個數列的反例好得多。
還有要注意的是選項(3)的說明。看到有老師說如果 $\langle b_n\rangle$ 收斂，利用夾擠定理左右兩邊極限會夾住 $a_n$, 所以 $\displaystyle \lim_{n\to\infty}b_n+\frac{4n-1}{n}=\lim_{n\to\infty}3b_n$, 得證 $\displaystyle\lim_{n\to\infty}b_n=2$. 雖然答案正確但這樣的論述大錯特錯。首先，夾擠定理並不是說夾住一個收斂數列的兩個數列會收斂到同樣的極限。第二，若要說明選項(3)是錯誤的（即$\langle b_n\rangle$不可能發散），應該是由假設它是發散而得到矛盾，怎麼是一開始就假設它是收斂呢？其實很多老師在這方面都有類似的錯誤。例如由題設的不等式就寫下$\displaystyle \lim_{n\to\infty}b_n+\frac{4n-1}{n}\le \lim_{n\to\infty}a_n$ 以及$\displaystyle \lim_{n\to\infty}a_n\le 3\lim_{n\to\infty}b_n$. 然後利用 $\lim_{n\to\infty}b_n\le 2$ 和 $\lim_{n\to\infty}b_n\ge 2$ 得證 $\lim_{n\to\infty}b_n= 2$. 雖然老師在取極限時很小心的將 “$<$” 改為 “$\le$”. 但這個論述還是有問題，因為當使用了$\lim b_n$以及不等式時，就已經將 $\lim b_n$ 看成是數字（即假設極限存在）了，試問若不是數字如何談不等式呢？或許老師會覺得 $\displaystyle \lim_{n\to\infty}b_n+\frac{4n-1}{n}\le \lim_{n\to\infty}a_n=2$ 這一邊已顯示 $\displaystyle \lim_{n\to\infty}b_n\ne\infty$. 沒錯這可說明 $\displaystyle \lim_{n\to\infty}b_n\ne\infty$, 但不表示它不會發散，因為發散不是只有往無窮大跑，還包括跳動方式無法收斂到一點。其實要知道一個數列是否收斂或發散並不容易。在高中階段只有兩種情況可以處理。一個就是當數列可以用$n$的形式寫下的情況，另一種就是用夾擠定理。夾擠定理是很強大的，也就是說當數列$\langle b_n\rangle$被兩個有同樣極限的數列 $\langle a_n\rangle$, $\langle c_n\rangle$ 夾住時，我們可以同時知道 $b_n$ 是收斂的而且知道其極限值。所以要用夾擠定理證明$\langle b_n\rangle$時，應找到合適的 $\langle a_n\rangle$, $\langle c_n\rangle$, 並好好的寫下 $a_n\le b_n \le c_n$, 然後說明 $\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n$, 再下結論說 $\langle b_n\rangle$ 是收斂的且其極限為何。千萬不要在未知收斂與否的情況下亂用 $\lim$ 符號。
最後為了讓學生更加了解收斂（極限存在）數列的定義， 我們可以進一步和學生談論以下將收斂數列$\langle a_n\rangle$稍微改變仍不影響其極限的兩個簡單方法：(1)將$\langle a_n\rangle$任意抽取出有限多項移除（其實只要不要將某項之後全部移除），所得的數列仍有一樣的極限；(2) 將$\langle a_n\rangle$任意插入有限多項，所得的數列仍有一樣的極限（這和本題所要評量的概念一樣）。
這一題，沒有什麼觀念要談，只是衝著補習班老師的一句大家都不教黎曼和，而來有感而發一下。這次的閱卷是歷年來工作最輕鬆的一次，不是考生人數下降的原因（因為每個人分配的閱卷數是一樣的），而是空白卷太多了，多到讓人憂心。這個因素很多，有可能如前面第4題所提：依資料判斷，此次數甲考生較偏向學測的低分組群。另外我強烈懷疑大多數教材將微積分移至高三上，再加上申請學校時程的改變，學生高三數學的學習幾乎等於0. 我也參與系上申請入學資料審查，絕大多數學生高一、高二數學成績相當優秀，但高三數學成績不及格者比比皆是。自己想想也真是幸運，不是這個年代的考生。想想要我一邊準備考試，接著參加考試，然後準備資料再參加甄試，又一邊念好高三那“深奧”的微積分，我可做不來。大人們為了自己的理想抱負要別人往前衝，卻不顧學生的壓力與學習成效，不僅影響了很多學生的升學權益，連整個高三（至少數學這一塊）的學習都空白浪費了。不談這些了，反正我也無能為力。不過說實話，這次閱卷的感覺很無力，因為考生的表現令人覺得好像只是為了參加考試有分數可以分發就好，沒幾個讓人覺得要拼命的將所學的表達出來。
真的如補習班老師說的，幾乎沒幾個考生會寫下黎曼和。真的是老師都沒教嗎？為什麼一個補習班老師會知道學校老師都不教呢？題目中已經很明確說明每一塊小長方體如何切割，只要將這些體積加在一起就可以了，為什麼學生不會呢？明顯的是學生將黎曼和當成一個深奧的專有名詞，根本弄不懂。或許真的和老師沒有教有關，也或許和 summation 符號 $\sum$ 延到高三才教，學生一時消化不了有關。不管怎樣，為了教學的完整性以及學生未來大學學習微積分的基礎，好好教學生如何將黎曼和寫下再轉換成定積分形式計算，真的很好用。以我自己的學習經驗，我從來沒有背那些求體積公式，要用時寫下每一薄片體積，寫成黎曼和，積分公式就自然出來了，其他的應用問題也都可應用自如。不過現在為了考試，老師學生只考慮什麼會考，什麼不會考，基本的功夫幾乎就被忽視了。
這一題寫出黎曼和 $\displaystyle\sum_{k=1}^n\left(20(\frac{15k}{n})+\frac{4}{9}(\frac{15k}{n})^2\right)\frac{15}{n}$ 後，可將 $15/n$ 視為將區間 $[0,15]$ 分割成$n$等分的 $\triangle x$, 而 $15k/n$ 就是在每等分中所選的 $x^*$. 所以可直接轉換成定積分 $\displaystyle\int_0^{15}(\frac{4}{9}x^2+20x)dx$. 有的老師將 $1/n$ 視為為將區間 $[0,1]$ 分割成$n$等分的 $\triangle x$, 而 $k/n$ 為在每等分中所選的 $x^*$, 所以改寫為定積分 $\displaystyle 1500\int_0^{1}(x^2+3x)dx$. 這兩個定積分只是差個變數變換，所得的值是一樣的。不過第一個較容易看出與原來面積函數的關係，建議還是用第一個方式來寫。當然了，第二個寫法是用黎曼和來看變數變換很好的例子，可惜高中沒有談變數變換。
這個題組的三個題目都有狀況，所以我一併來談。第15題能將函數寫對的已不多了，接下來便是看學生微分的能力了。原本以為分式的微分是新課綱內容，老師應該會好好讓學生練習。確實會寫到這裡的考生都會“背”分式微分的公式，為什麼我把背這個字標起來呢？因為大部分的考生只會分子有$x$的分式微分。題目已暗示將 $\displaystyle f(x)=\frac{x^2-9x+16}{9x-x^2}$ 寫成 $\displaystyle\frac{16}{9x-x^2}-1$, 考生也都寫成這種形式了。結果絕大多數的考生在微分時，又將函數改回原來分子為二次式的分式來微分，完全不知道部分分式形式的微分會簡單很多。依照學生的計算能力，大家應該可以猜出來了吧，分子分母皆為二次式的分式微分是怎樣的慘不忍睹啊！用這樣方式微分的考生幾乎沒一個作對的，但又偏偏絕大多數的考生都是這樣做的。閱卷的教授都百思不解，難道學生連最基本的常數微分為$0$都不知道嗎？結論是學生可能沒作過分子為常數的分式微分，不過這回課綱還加了微分的 chain rule, 老師應該會練習吧！很可怕吧！原本以為學生微積分理論不熟，最會的就是微分的操作了，沒想到最基本的加法法則也不會用，更別談分式微分了。
第16題，有一些老師顧忌有超綱嫌疑。不過閱卷教授都沒有這樣的疑慮。既然教了分式微分，不去用它，那學它幹嘛？我對108課綱最大的質疑也在這兒。先撇開設限太多的議題，卻又加了一些怪怪沒什麼用的東西硬要學生學習。前面提過三次配方的問題，這個技巧在後來的學習都沒用，只為了找三次函數的對稱中心，不過大家卻把重心放在配方，連對稱中心的意義都不了解。一次近似直線也是一樣，對學生來說僅是個名詞，知道了就沒再用。後來還有什麼 euler number, 二次曲線旋轉有 $xy$ 項, 泰勒展開式 以及一大堆奇奇怪怪的意涵。這些只能教，但不能用，那學生學它做啥？現在若又說可教分式微分但不能應用，那我真要罵人了！猶太人說：「讀很多書的人，如果不會用書上的知識，那他只不過是隻馱著很多本書的騾子。」又扯開話題了，這一部分若前一題正確的考生（不過真的很少了），大致上回答的都 OK! 還有些考生雖不會微分，但由函數是二次式的倒數，想到用二次式的遞增遞減處理。看來超綱的說法是多慮了。
第16題，還有些老師在意著遞增遞減的範圍的寫法（該用開區間或閉區間），趁這個機會說說我的看法。這一題依題意，由於三角不等式的關係，函數 $f(x)$ 的定義域為開區間 $(1,8)$. 由於當 $\displaystyle 1< x<\frac{9}{2}$ 時 $f'(x)< 0$, 而當 $\displaystyle \frac{9}{2}< x< 8$ 時 $f'(x)> 0$, 所以有老師疑問該寫“在 $\left(1,\frac{9}{2}\right]$ 遞減, $\left[\frac{9}{2},8\right)$ 遞增”；還是“在 $\left(1,\frac{9}{2}\right)$ 遞減, $\left(\frac{9}{2},8\right)$ 遞增”？其實兩個都可以，這和定義有關，老師們不必太在意。首先對於 $f(x)$ 在一個區間是遞增 (resp. 遞減) 其定義為對任意在此區間的兩點 $x_1,x_2$, 若 $x_1>x_2$, 則 $f(x_1)\ge f(x_2)$ (resp. $f(x_1)\le f(x_2)$). 定義完在區間的遞增遞減後，我們可以定義在一點的遞增遞減。如果 $a$ 是函數 $f(x)$ 的定義域中的內點，且可以找到一個包含 $a$ 的開區間使得 $f(x)$ 在此開區間為遞增 (resp. 遞減), 則稱 $f(x)$ 在 $a$ 這一點為遞增 (resp. 遞減)。注意以此定義，題目中的 $f(x)$ 在 $x=9/2$ 不是遞增也不是遞減。現在應該知道為什麼說兩個都可以了吧！用區間的看法，說“在 $\left(1,\frac{9}{2}\right]$ 遞減, $\left[\frac{9}{2},8\right)$ 遞增”當然沒問題。但另一方面說 “$f(x)$ 在 $\left(1,\frac{9}{2}\right)$ 這些點遞減, 而在 $\left(\frac{9}{2},8\right)$ 這些點遞增”也沒錯。高中由於沒有談在一個點的遞增遞減，所以大多數教科書用前者。不過在大學，我會用後者，否則學生看到“在 $\left(1,\frac{9}{2}\right]$ 遞減, $\left[\frac{9}{2},8\right)$ 遞增”，問我在 $x=9/2$ 到底遞增遞減，又要解釋半天。
在閱卷場上，一些教授看到全中教新聞稿關於17題的疑義（閱卷老師都很認真，大家會注意一些外界的解法與意見），真的傻眼。我們能體會老師們希望能幫學生爭取分數的心情，但是那些偏離數學的論述就大可不必。 幾年前也有某些學校的數學老師集體提出申覆，內容大概就是老師們為了方便讓學生會操作，所以忽略了一些細節，以至於該題無法正確作答。簡單來說，就是老師未教正確觀念，導致學生做錯，希望能有補救。這次看到全中教新聞稿強調 「第 17 題目不清，答案可能不僅唯一正解。因題意不清，學生無法準確判斷要利用哪一個位置求一次估計，建議該題若學生使用 4.96 附近求得的一次近似估計值，皆應給分(答案非唯一，將有數個正解)亦或者此題應考慮送分。」我的解讀是，老師們教一次估計，只是將它當個專有名詞（就像黎曼和）教學生套公式代點就可以了，而忽略了它的真意。這一點，我覺得補教界的新聞稿寫得比較好，明明白白的說我們沒教黎曼和。後來不知全中教是否有提出申覆，我以下所說當然和大考中心無關（說過我是無足輕重的人物）。首先，我和大多數數學教授持一樣觀點，大考數學一定要有非選題。因為數學不能僅由對、錯單一標準來評量。而在我參與的閱卷工作中，大家都謹守這樣的認知。所以請放心，怎樣是合適的答案與作法，都會依公平性與正確性不犧牲學生該得權益訂定。這一題沒有送不送分的問題。讓我們談一談一次估計吧！
前述新聞稿所提“使用 4.96 附近求得的一次近似估計值，皆應給分”就明顯不了解一次估計在做什麼。今天 $f(x)$ 在 4.97 的值與 4.96 的值一樣難求，那幹嘛用一次估計（還要多算在4.97的微分值）直接算 4.96 的值就好了。大家都在談素養，想想這樣的情境，你需要知道此函數在4.96的值，卻沒有計算機，會突然有個聲音告訴你要用 5 的一次近似嗎？一開始介紹一次近似時，當然要先給點，練習一下在該點附近的函數值的一次近似。之後，應該要學生了解，它在實際一些情況能讓我們較輕鬆的估計一個函數值。這時如何找合適的點估計，當然是必要的數學素養。或許有的老師覺得有了計算機，為何要學一次近似？說得很有道理，不過課綱又說要學啊！課綱應該有要求用計算機驗證一次估計的值與實際值的差異。若連代入一次估計的一次函數都要用計算機，那一次估計就畫蛇添足了。
閱卷時我們也聽說這一題 $f(x)=\displaystyle\frac{16}{9x-x^2}-1$ 的一次估計有補習班老師利用先算$9x-x^2$的一次估計，再代回求值（說過閱卷老師都很認真）。這當然也是一種估計值的方法，但它不是 $f(x)$ 的一次估計。或許你會發現，這樣的算法比 $f(x)$ 的一次估計準（更接近原值）。沒錯，一次估計是強調它計算的容易（只用到加法與乘法，而用分母的一次估計要用到除法），而不是其準確度。籠統來說一次估計應該是最簡單計算，但最不準的（這也合理，我們都知道沒有不勞而獲的道理）。舉一個最極端的例子，若我們要估計 $\displaystyle g(x)=\frac{1}{x}$ 在 $x=0.9$ 的值, 利用一次估計 $g(0.9)\approx g(1)-g'(1)\times 0.1=1.1$, 而分母 $x$ 用 $1$ 做一次估計在 $x=0.9$ 仍為 $0.9$, 所以這樣是等同於直接算 $g(0.9)=1/0.9$ 當然比較準確，不過計算上就真的要算這個除法。不管怎樣，教一次估計千萬別忘了這個重點。就是利用鄰近較好求的點，簡單利用加法與乘法來幫我們求得近似值；而不是隨便找個點（或是靠別人幫你找點）套公式了事。
有做17題的同學就又少之又少了。做錯的考生中知道用 $5$ 求一次估計但式子寫錯的遠比會寫式子但不知用哪一點的多。所以問題不在於學生知不知道用哪一點做一次估計，而是根本不知道什麼是一次估計。前面提過這次課綱的很大問題，就是許多數學讓你知道就好，但又因為不敢觸及更深入的問題，就停在那兒。結果大家就像教專有名詞一樣，提過就好。試想學生沒有充分了解與使用，結果什麼也沒學到，是不是像馱著沉重書籍的驢呢？