此次考題，多數認為較前兩年題目難。平心而論，若只研讀數學 B 內容的考生，應該無法考好這份考題。不是內容超綱的問題，而是所接受數學訓練，也就是數學成熟度的問題。就像有些人聲稱學習數B的內容，就能在高三學習數乙的微積分，這一點我也極度的懷疑。這不是數B所學內容夠不夠學習數乙的問題，而是數B所學習數學的訓練，不足以讓學生充分理解數乙微積分的內容。從這個角度來看，這份考題有很多抽象符號操作的問題。已經談論過很多次了，即使概念容易，但只要牽涉到抽象的符號操作，大部分考生（即使數A的考生）都表現不佳。 考試成績出來，數B的級矩甚至低於也算難的數A，其中選填17題的答對率還僅有 $1\%$。對於一般數學需求度低，而修習數B的考生，確實令人覺得委屈。不過換個角度來看，這樣的考試應該會讓更多的學生修讀數A課程，也不錯！不過這樣設置數A、數B兩個考科的用意已經越來越偏向於，讓數A沒考好的考生多了一個表現數學能力的機會。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 58 | 81 | 30 | 85 | 73 | 64 | 48 | 21 | 51 | 12 | 9 | 16 | 27 |
拿這一題出來討論，只有一個原因，想知道為何本題答對率這麼低。將此題置於第一題，不只出題者，應該大部分的老師都會認為這一題答對率應該是暴衝的吧！題目沒有冗長的文字，簡明扼要，應該不是不懂題意。本題答對率和今年數A第2題（應該比較難）相近，但不管是前 $20\%$ 的最高分組答對率（Pa）或前 $33\%$ 的高分組答對率（Ph）皆低了將近$10\%$。低分組在本題表現比數A第2題好是可以理解的（因本題比較不抽象，容易操作），真難以理解高分組的表現為何明顯較差。 或許有人認為是數A、數B高分群程度上的差異，但對於簡單的問題，不應有如此的差異。
此題一看，或許覺得是等差級數的問題，大部分考生就直覺的加上去，看哪一位會是在第90百分位。是不是在算級數時計算錯誤（試卷有附公式，應不是公式代錯）？其實出題者，真的打算這一題送分，問的是第90百分位，而不是問比較中間的百分位數，很明顯的就是希望大家倒著算會比較快。老師不妨統計一下，學生看到此題到底是乖乖照著定義正著算，還是從大到小倒著算。若有很大部分的學生是正著算的，表示學生對於數學名詞的定義了解的方式太死板了不夠靈活。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 49 | 88 | 13 | 94 | 74 | 45 | 22 | 9 | 75 | 20 | 29 | 23 | 13 |
答對率比第1題低了近$10\%$，不過最高分組的得分率卻比第一題高了近$10\%$，是該組全卷最高的。可以確定的是本題得分率是被低分組考生拉低的。這也造成本題有整卷最高的鑑別度（$D=75\%$）。這表示高分組與低分組對這個問題的理解有顯著的差異。主要的因素，應該就是我一再強調的，對符號（非數字）的理解能力。 看到這麼多考生對於 $0 < b=\log a<1$, $\log b<0$ 這個對數的基本常識都不知道，顯然對對數相當不熟悉。這讓我忍不住想發點牢騷：這個部分應該屬於高一共同的內容，不過高二數B就不像數A繼續討論對數律以及對數函數，而直接跳到對數的應用。試想以目前狀況來看，學生在對對數尚不夠了解的時候，談論應用，對學生而言真的是淪為背公式而已。曾聽說有老師公開說對數的某某性質沒有用，可以不必教。真的很不妥。其實讓學生知道這些性質，不只能讓學生更了解對數，也能讓他們更熟悉對數。學習數學絕不是只學以後會用的東西就好，多方的學習理解才能提升一定的成熟度。當我們看到這一題低分組的答對率只有$13\%$，若再進一步看看選項分析（這裡從略）發現竟有接近$10\%$的低分組考生，選擇了最不可能的選項(5)（連 $b<0$ 都可取 $\log$），不得不令人歎息。對他們來說 $\log$ 就像題目裡的 $a,b,c$ 只是一個符號而已。
對於符號操作有困難，程度較不好的學生，或許老師可以教學生代值試看看。例如代 $a=2$，利用題本後面所附的值，可得 $b=\log 2$ 約等於 $0.3$。再利用 $c$ 約等於 $\log 0.3=\log (3\times 10^{-1})=-1+\log 3$ 約等於 $-1+0.48$ 所以 $c$ 小於 $0$（不過這裡要用對數律）。若知道 $\log x$ 是遞增的就更好了。可以由 $1 < a <10$ 取 $\log$ 得 $\log 1<\log a<\log 10$，知道 $0< b <1$。再利用 $b<1$ 取 $\log$ 得到 $\log b<\log 1$，即 $c<0$。 對於指數較熟悉的學生也可以直接換回指數來處理，例如由 $1=10^0< a=10^b<10^1$ 得到 $0< b<1$。總之，不要直截了當告訴學生 $c<0< b<1$，如此一來不止更了解對數，也能更進一步了解對數律等特性。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 26 | 51 | 11 | 63 | 30 | 16 | 13 | 9 | 40 | 33 | 14 | 3 | 4 |
光從題目來說，個人認為此題是單選題中最難的（沒想到後來殺出了一個第7題）。估計應該有許多考生不知如何掌握 $\overset{\displaystyle{\rightharpoonup}}{AB}$，直白來說就是不知道它是什麼。事實上 $A,B$ 是 $(0,0),(1,0),(0,1),(1,1)$ 為頂點的正方形（和今年數A第17題一樣的正方形）內任意兩點，所以$\overset{\displaystyle{\rightharpoonup}}{AB}$是這正方形內任意可能的向量。也就是可以用 $(x,y)$ 其中 $-1\le x\le 1$, $-1\le y\le1$ 這樣的方式來表示 $\overset{\displaystyle{\rightharpoonup}}{AB}$。最後就是求$x,y$在這範圍內 $\sqrt{(x-2)^2+(y+3)^2}$ 的最大值。又是需要抽象符號操作的問題（還好這題在單選題，若數字改一改擺在選填題，一定更慘），這方面較薄弱的考生，應該是一開始不知道$\overset{\displaystyle{\rightharpoonup}}{AB}$是什麼（不會設代數符號表示），而在這個地方卡關。老師可以嘗試一開始給 $\overset{\displaystyle{\rightharpoonup}}{AB}=(x,y)$ 其中 $-1\le x\le 1$, $-1\le y\le1$，看學生會不會繼續完成，就能理解學生基本上問題在哪。
其實老師可以鼓勵學生用圖示的方式處理本題，或許能讓對向量不甚了解的學生，更一步了解向量的特性。一開始讓學生在題目 $A,B$所在的正方形內任點 $A,B$ 兩點，連成向量 $\overset{\displaystyle{\rightharpoonup}}{AB}$，如圖：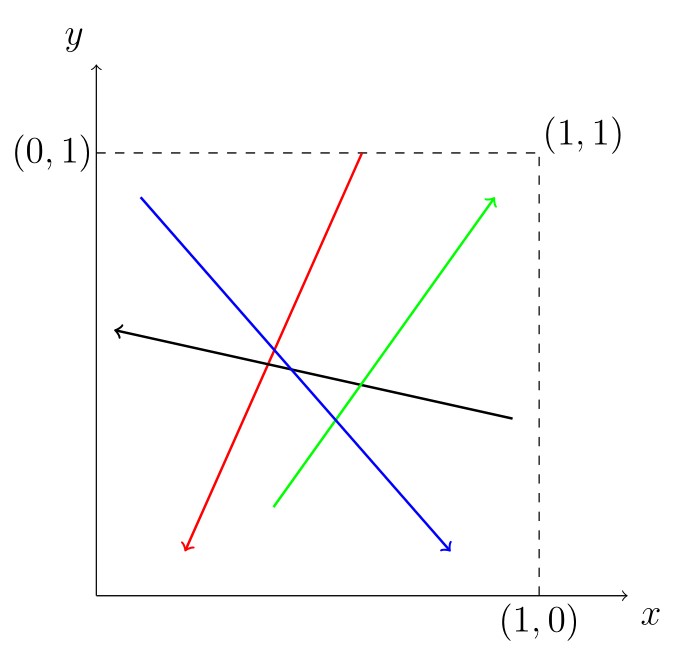
。接著將這些向量移到起點為原點的位置，看看學生是否理解，事實上$\overset{\displaystyle{\rightharpoonup}}{AB}$可視為起點在原點，端點在以 $(1,-1)$, $(1,1)$, $(-1,1)$, $(-1,-1)$為頂點的正方形內，如圖：
。最後題目問的 $\overset{\displaystyle{\rightharpoonup}}{v}+\overset{\displaystyle{\rightharpoonup}}{AB}$ 的長度，就是將 $\overset{\displaystyle{\rightharpoonup}}{AB}$ 的起點移到點 $(-2,3)$ 後端點與原點的距離，如圖：
。不難看出，在左上角的頂點$(-3,4)$距離原點最遠。這一部分也可讓學生以畫圓的方式看出。這一次數A、數B，不約而同的都沒有有關圓的問題，不妨在這一題（或數A第17題）帶入利用圓來判斷遠近的概念。
很多人看到這一題，認為是國中也會做的題目。不過出題者把它擺在第6題（單選的最後第2題），應該認為它並不容易。事實上本題答對率不高，也不像預期如國中題目有高分組答對率暴衝的跡象發生。有趣的是，本題各組的答對率以及鑑別度與今年數A第5題（也是單選的最後第2題）幾乎一樣，對考生而言應該不算容易。 關於本題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 37 | 67 | 13 | 80 | 45 | 29 | 20 | 9 | 54 | 35 | 16 | 9 | 11 |
會拿這一題出來談，主要原因是，個人認為這一卷的單選題中第1,3,6題是很適合數B的考題。會這樣說，並不是因為它們都是情境題（其實基本上我是很不喜歡情境題），而是它們並沒有牽涉艱澀的數學問題，但卻能評量考生的數學素養。很多人把素養題和情境題混為一談。有些題目為了和素養沾上邊，硬加上一些情境或當時流行的話題，就被一些人吹捧的順應時事、與生活貼切等；而完全不論情境是否合理，更不論裡面的數學是什麼。從情境的角度來說這一題也很牽強。耶誕樹造型燈飾的設計還算合理，但問的問題就很奇怪。誰會去在意燈飾與地板截出的線段長佔地板的幾分之幾呢？不過，我覺得它是很好評量數學素養的題目。數學素養，或許大家的定義不同，個人覺得它不像我們常提的文學素養，要懂很多的文學著作；而是比較像前面談的數學的成熟度。在論述的時候是否邏輯清晰有條理，處理問題時能否掌握問題的重點等。這一題，應該就是課綱中所謂三角比的問題，雖然就是國中相似三角形的比例關係，不過大部分考生面對的困難就是能否看出這個重點，找到能比較的三角形。題目中好幾個三角形，如何排除不必要的訊息，有效的處理問題，也是數學訓練重要的一環。曾經談過，看過許多老師在教學生解題時，都先把題目中給的條件所能得到的性質列出來，而沒有先看看問題在問什麼。這會造成學生在解題時，往往會因為過多的訊息，而不知所措。
老師可以和學生確認哪些是不必要的訊息，哪些是重要的。在知道三角形$PCD$和一樓（樹幹部分）是沒必要，以及樓層等高、地板等長是必要的，就可把原圖簡化如圖：
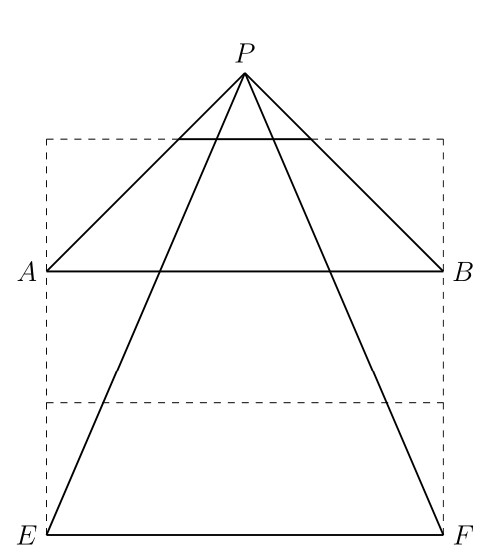。接下來，提醒各樓層地板平行，以及三角形$PAB$截出地板的$\dfrac{1}{3}$的訊息後，學生應該就不難處理此題了。若能進一步釐清是否需要等腰三角形的假設就更好了。對於程度較差的學生，用這樣的方式了解學生哪方面的能力較薄弱，會比直接教他們會做這一題好得多。
看到有人戲稱此題沒考什麼數學，只考邏輯，連小學生都會做。這個說法不是很恰當。儘管是評量邏輯推理問題，也有難易之分。這一題算是蠻難的，甚至在網路上看到有些老師在處理此題排除選項(5)的過程，也發生邏輯上的錯誤。這些錯誤大多發生於不自覺的多加了一些假設。例如，有些會誤以為東區的溫度都比西區高，也有人以為兩區高、低溫一定會發生在不同溫度範圍（可以用這假設得到一些可能的狀況，但不能用此假設去排除一些情況）。這一題也是不錯的素養題，不過處理問題所需數學的成熟度較高，或許較合適於評量數A的考生。可惜數A有太多數學內容要評量，應該沒有空間評量這類題目。對於數B的考生，相信有許多在考完後仍不理解這一題在問什麼。這從這題的答對率以及鑑別度就能看出。 關於本題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 24 | 11 | 30 | 15 | 10 | 10 | 11 | 13 | 15 | 5 | 0 | -1 |
連前 $20\%$ 的最高分組答對率也僅有 $30\%$，這在單選題是很少見的（前一次是111年數A第3題），可見連高分組的考生也有困難理解本題。而最低分兩組鑑別度（D4）也發生少見的負值。當然了這個鑑別度沒有什麼意義，大家都亂猜，只是最低分組的考生猜對的比例高一些罷了。再從考生做答的選項分析來看，我們更能確定大部分的考生真的不知道這一題在問什麼，他們只憑直覺選了選項並沒有多花時間進一步理解題意（111年數A第3題也有類似情況）。此題大考中心提供的選項分析如下：
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | 8 | 47 | *15 | 15 | 17 |
| H | 0 | 2 | 33 | 24 | 15 | 26 |
| L | 0 | 8 | 54 | 11 | 16 | 11 |
最不可能的選項(2)竟然是最多人選的選項：題目問的是兩區溫度的最大值在各溫度區間的天數，卻被解讀成各溫度區間兩區天數的最大值。若是如此，當月的天數不就有35天，超過了題目所說的30天。這麼多考生選了這個選項也不去考慮其合理性，顯現了對這個題目的無奈吧！應該沒有老師會針對邏輯這一塊特別來教導學生，也無從教起。這都得仰賴學生平時多思考所累積的數學素養（成熟度）。我也不知如何僅從本題就能建議老師健全學生邏輯推理能力的方法。以下僅說明如何用正確的邏輯推理方式來判斷各選項的可能性，並舉例確定選項(3)確實可以符合題目所給的東、西兩區高溫的分佈情況。
題目問的是哪一個選項有可能發生，當然了因為是單選題，若能針對某個選項找到一個例子符合題設，就可確定是該選項。不過選項這麼多，除非能排除一些選項，否則每個選項都得嘗試舉例，實屬不易。所以這類問題，最常用的方法就是排除法，儘量排除一些選項。剩餘的選項若一時找不到排除的因素，再嘗試利用例子看看能否找到可能的選項，或找到進一步可以排除的因素。最好的情況是，能排除到僅剩下一個選項，也就可以不必舉例了。讓我們從最容易判斷的大於等於36度的情況開始，依圖表所示在30天中，東區有5天，而西區沒有任何一天，大於等於36度。所以很明顯的兩區就只有這5天氣溫的最大值會大於等於36度。因此可以確定題目中的$D$等於$5$，我們馬上可以排除選項(1)。同樣的道理，在氣溫小於24度的情況，東區沒有任何一天發生，而西區有3天。這3天是兩區唯一氣溫小於24度的情況，但這3天東區的氣溫一定大於等於24度，所以這3天最高溫會發生在東區，也因此該都市對高溫不會有低於24度的情況，也就是說題目中的$A$等於$0$。我們因此也排除了選項(2),(4)。最後僅剩考慮選項(3),(5)，這才是本題較難的部分（不過全體選這兩個選項的考生總共只有約$30\%$）。
要如何排除選項(3)或(5)呢？可以讓學生嘗試依東、西兩區高溫的分佈情況排排看。其實不難發現兩區最高溫在24度到29度之間的情況只有可能發生在東區的那11天中。這是因為這個月其他的19天，東區的溫度都大於29度。所以那19天的最高溫，絕不會是在24度到29度之間，也因此只有那11天該都市的最高溫有可能在24度到29度之間。要注意這並不表示那11天該都市的最高溫都在24度到29度之間，因為有可能11天中有某些天西區的溫度大於29度，所以我們只能確定該都市的最高溫在24度到29度之間的天數會小於等於11天，也就是說 $B\le 11$，也因此成功的排除了選項(5)。老師可以嘗試問問學生，同樣的論述是否適用於西區溫度在24度到29度之間的那12天？也就是，能否確定兩區最高溫在24度到29度之間的情況只能發生在西區的那12天中？答案是否定的，因為那12天以外有3天西區的溫度低於24度。若那3天的某幾天東區的溫度在24度到29度之間，那麼該都市在那幾天的最高溫也會在24度到29度之間。
我們也可利用30度到35度這個區間的情況，排除選項(5)。這是因為東區溫度在30度到35度的這14天中，該都市東、西兩區的最高溫也會發生在在30度到35度這區間。 原因是，這14天中的某幾天若最高溫發生在東區，那當然該都市這幾天的最高溫就在30度到35度之間；而其他天若雖然最高溫發生在西區，但西區的氣溫不可能高於35度，所以西區的氣溫仍然在30度到35度之間，所以該都市這14天的最高溫都在30度到35度之間。當然了，東區低於30度的那幾天，西區有可能在30度到35度之間，所以我們只能下結論 $C\ge 14$，這也因此排除了選項(5)。老師可以嘗試問問學生，同樣的論述是否適用於西區溫度在30度到35度之間的那15天？
最後依慣例，為了完整性，我們舉例說明選項(3)確實可能發生（考試時不需此步驟）。由於只在意天數，下表中，我們將東區的溫度依題設的天數由大排到小。至於西區的溫度，由前面討論，我們只要在東區24度到29度的11天期間有兩天是超過29度，其餘9天不要超過29度即可。最後剩下的空白處就可以自由將剩餘西區的溫度填入（需滿足西區溫度分佈的天數），都會符合選項(3)。
| 日期 | 1~5 | 6~19 | 20~21 | 22~30 |
|---|---|---|---|---|
| 東區溫度 | 36 | 30 | 24 | 24 |
| 西區溫度 | 30 | 24 |
第9題，當成多選的第二題，出題者應該認為這題在多選題中應該是比較容易的題目。不過從考生的表現來看並非如此，本題的得分率在多選題中是最低的。從多選題的選項分析來看，低分組各選項被圈選的比例都差不多，合理的解釋應該是他們猜答的情況比較多。所以低分組在多選題各題的得分率都差不多，也就是說多選題得分率低，大多是高分組的得分率低所造成。此題低分組的得分率並不是多選題中最低的，但高分組的得分率不只是最低的，而且比次低的題目低了 $12\%$。第9題的得分率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 29 | 44 | 18 | 51 | 31 | 24 | 21 | 16 | 12 | 26 | 20 | 7 | 3 | 5 |
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | 39 | *71 | 35 | 42 | *39 |
| H | 0 | 32 | 91 | 15 | 36 | 41 |
| L | 0 | 45 | 52 | 52 | 44 | 38 |
多選題算的是得分率。P為$29$表示本題全體平均分數為5分的$29\%$，以下依此類推。多選題的統計資料多了一個 T, 它表示此題5個選項全對的考生所佔的比率。令人訝異的是本題僅有 $12\%$，可見本題連高分組的考生大部分都不知如何處理。不過若只問其中一個選項，就拿答得最不好的選項(5)好了（僅有$39\%$答對），問學生商式為多少，相信會有更高比例的學生能正確得到商式。所以本題答得不好的原因，以我事後諸葛來判斷，不是學生不會多項式的除法，而是不會利用抽象的除法原理的表示方式來找到本題的處理策略。之前提過108課綱將一般多項式相關的運算弱化了，而去強調僅局限於三次多項式的課題。看到最直接的選項(1)竟然有高達$39\%$的考生圈選這個錯誤選項，就可看出學生對於多項式這部分理解能力之薄弱。純粹個人意見認為，對於目前數B的考生學習情況來說，此題改為僅問選項(5)的商式、餘式會比較合適。至於原題應較適合數A，甚至比今年數A第14題（用到課綱未提到的同餘概念）更合適。
相信大部分的考生都知道本題的解題策略應不是把每個選項展開再做除法。為了解釋一般處理這個問題的有效方法，我們就不能只拿具體的多項式來解釋，而需用抽象的一般形式來表達。本題的問題便是如果已知多項式 $f_1(x), f_2(x)$ 除以 $g(x)$ 的商式與餘式，能不能知道 $f_1(x)+f_2(x)$ 除以 $g(x)$ 的商式與餘式。我們可以先寫下 $f_1(x)=g(x)h_1(x)+r_1(x)$, $f_2(x)=g(x)h_2(x)+r_2(x)$，即 $h_1(x), h_2(x)$ 分別是 $f_1(x),f_2(x)$ 除以 $g(x)$ 的商式且 $r_1(x), r_2(x)$ 分別是 $f_1(x),f_2(x)$ 除以 $g(x)$ 的餘式。將上面兩式相加我們可以得到\[f_1(x)+f_2(x)=(g(x)h_1(x)+r_1(x))+(g(x)h_2(x)+r_2(x))=g(x)(h_1(x)+h_2(x))+(r_1(x)+r_2(x)).\] 由於 $r_1(x)+r_2(x)$ 的次數仍小於 $g(x)$ 的次數，故知 $h_1(x)+h_2(x)$ 就是 $f_1(x)+f_2(x)$ 除以 $g(x)$ 的商式，而 $r_1(x)+r_2(x)$ 就是 $f_1(x)+f_2(x)$ 除以 $g(x)$ 的餘式。簡單來說就是兩多項式相加後做除法所得的商式就是將原來的商式相加，所得的餘式就是將原來的餘式相加（餘式這部分就是今年數A第14題所用同餘的概念，不過該題多個乘法，又稍微複雜一點）。
知道上面的性質後，我們就可以很快的算出此題各選項的商式與餘式了。選項(1)當然沒問題，商式為 $2(x^3+7x^2+x+3)$ 餘式為 $0$。（依然對此選項竟然有高達$39\%$的考生圈選感到訝異）。選項(2)可視為$(x^3+7x^2+x+3)(x^2+5x+1)$ 加上 $-x$，因為 $-x$ 除以 $x^2+5x+1$ 的商式為 $0$，餘式為 $-x$，所以這個選項的商式為 $(x^3+7x^2+x+3)+0$，餘式為 $0+-x$。同理由於 $x^2$ 除以 $x^2+5x+1$ 的商式為 $1$，餘式為 $-5x-1$，所以選項(3)的商式為 $(x^3+7x^2+x+3)+1$，餘式為 $-5x-1$。至於選項(4)，用到前面所提 $-x$ 的 商式為 $0$，餘式為 $-x$，可以得 $(x^3+7x^2+x+4)(x^2+5x+1)-x$ 除以 $x^2+5x+1$ 的商式為 $(x^3+7x^2+x+4)+0$，餘式為 $0-x$。最後一個選項可視為$(x^3+7x^2+x+4)(x^2+5x+1)$ 加上 $-x^2$，因為 $-x^2$ 除以 $x^2+5x+1$ 的商式為 $-1$，餘式為 $5x+1$，所以這個選項的商式為 $(x^3+7x^2+x+4)-1$，餘式為 $0+5x+1$。
從前面一直談論抽象符號運算的角度來看，這一題考生的表現當然不會好。全體答對率 $31\%$ 只比第9題高了 $2\%$，不過從分組資料來看，高分組和低分組在這兩題表現是有差異的。以下提供本題答對率的分組資料，和第9題的資料相比較，我們可以看出學生了解多項式與指對數程度上的差異。
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | T | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 31 | 56 | 14 | 68 | 36 | 22 | 17 | 12 | 15 | 42 | 32 | 14 | 5 | 5 |
從數學理論的深淺來說，當然是指對數比多項式來的深。低分組在這一題表現的比第9題多項式差是想當然耳。而高分組在本題的表現優於第9題（尤其前$20\%$的最高分組更多出了$17\%$），應該就是他們較常做這類題目的練習，較熟悉此類數學的定義方式。本題符號多，看似複雜，不過出題者並沒有刁難考生，幾乎只考定義，僅有選項(2)需要稍微計算一下。其實選項(2)只要願意算 $0.95$ 的平方大於 $0.9$應該就能判斷它是錯的。高分組有$22\%$圈選此選項，令人錯愕（或許是慣用計算機，降低了估算能力）。選項(3)、(4)、(5)都只是問“5年中每年平均減少$5\%$”這一個概念。照理來說考生若知道這一點，那麼這三個選項的答題狀況應該很一致。不過從以下所列的選項分析會發現，沒錯！選項(4)、(5)的答題狀況確實相當一致，但選項(3)卻有所偏差。看來很多學生還是不清楚這裡“平均”的意義，而被誤導了。
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 1 | *65 | 39 | 54 | *60 | *59 |
| H | 0 | 87 | 22 | 36 | 77 | 73 |
| L | 1 | 45 | 50 | 63 | 48 | 47 |
其實平均成長率的問題在109年指考數乙非選第一題就已考過。
首先學生要了解一些文字的敘述，或多或少每個人會有解讀上的差異。而以數學方式定義的好處，就是讓它一致。因此在這類文字題也請學生不要拘泥於一些專有名詞。例如不要因為看到“二氧化碳排放當量”就覺得不熟悉這個議題，而放棄作答。也不要看到“平均”這個字眼，就認為是一般的算數平均。一切都應該以題目給的數學定義處理。這裡就不去談這些名詞的意義，直接用數學的定義處理。其實出題者先問選項(3)後，才問選項(4)、(5)，確實會讓考生在不了解 $-0.07,p,q,r$之間的關係下，被“平均”這個字眼誤導了。順序上應該是先問選項(4)、(5)再問選項(3)比較好。選項(4)只是將原式 $Y=(1-0.05)^4X$ 移項開4次方根即可（僅$60\%$的考生答對，令人吃驚）。選項(5)需利用各年排放成長率的定義得到 $A=(1-0.07)X$, $B=(1+p)A$, $C=(1+q)B$ 以及 $Y=(1+r)C$，因而得知 $Y=(1+r)(1+q)(1+p)(1-0.07)X$ 再由已知 $Y=(1-0.05)^4X$ 得到 $(1+r)(1+q)(1+p)(1-0.07)=(1-0.05)^4$。若了解何謂平均成長率，應該馬上知道選項(3)是錯的，不過它錯在哪呢？其實反應快的學生應該由選項(5)知道這是算幾不等式，也就是說$\dfrac{1}{4}((1+r)+(1+q)+(1+p)+(1-0.07))$ 會大於等於 $\sqrt[4]{(1+r)(1+q)(1+p)(1-0.07)}=\sqrt[4]{(1-0.05)^4}=1-0.05.$ 事實上，因為有一項 $1-0.07\ne1-0.05$，我們知道等式不可能成立。最後化簡得 $\dfrac{1}{4}(r+q+p-0.07)>-0.05$。
第12題，當成多選的最後一題，表示出題者認為這是多選題中最難的題目。確實也是如此，最後兩個選項能完整論述的考生相信不多。不過考生的表現並不差，此題的得分率竟是多選題中第二高的。會有這樣的結果，個人認為是選項的安排。本題很符合我一向建議多選題的選項安排：前三個選項評量較基本的問題，後兩個選項再評量較深入的問題。本題前三個選項只是評量基礎的機率問題，卻也引導考生發現其規律性，因而可合理推論後兩個選項正確與否。這樣的安排，大大提升了低分組考生在此題的答對率，事實上在多選題中，低分組在本題的得分率是最高的。不過高分組的表現並不如預期，特別的從大考中心提供的選項分析裡，可發現連簡單的選項(2)，高分組都有 $25\%$的考生錯答，大部分考生是否這一題是用正確的方式處理，恐怕並不樂觀。以下是大考中心提供第12題的選項分析：
| 組別 | 未答 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| T | 0 | *76 | 35 | 27 | *76 | 37 |
| H | 0 | 92 | 25 | 10 | 91 | 29 |
| L | 0 | 58 | 45 | 44 | 58 | 44 |
對於數B的考生，本題實際計算了 $b_1=b_2=\dfrac{1}{4}$ 以及 $c_1=c_2=\dfrac{1}{4}$，而推測對所有正整數 $n$ 皆會有 $b_n=c_n=\dfrac{1}{4}$，來處理本題尚屬合理。不過這裡，我們依然照慣例，提供完整、正確的做法。一開始看到題目，會想到轉移矩陣，不過高階轉移矩陣高中並未探討且這一題不必這麼處理，這裡就略過不談這個方法。這類問題，應該都是用數學歸納法處理，我們先從 $n=1$ 開始，看看如何推導到 $n=2$ 的情況，大致上就可以知道如何用數學歸納法證明了。首先依題意，原來在$A$的位置，所以4個方向中有有兩個方向會停留在$A$，得$a_1=\dfrac{2}{4}=\dfrac{1}{2}$。另外，從$A$到$B,C$各有一個方向，所以$b_1=c_1=\dfrac{1}{4}$。又不可能從$A$一步到達$D$，故$d_1=0$。下一步，我們要從$n=1$的結果推導到$n=2$的情況，這是要推導到一般情況重要的步驟，所以儘量列式，不要先代值。由於我們要了解的是 $b_n,c_n$，所以先關心如何到達 $B$ 和 $C$。到達$B$有可能是從$A$到$B$，這個情況的機率是$\dfrac{1}{4}$，不過第一步留在$A$的機率是$a_1$，所以$A\to A\to B$ 這部分的機率是$a_1\times\dfrac{1}{4}$。而$B$留在$B$的機率為$\dfrac{1}{2}$，故$A\to B\to B$ 這一部分的機率是$b_1\times\dfrac{1}{2}$。接著$A\to C\to B$ 的機率為$c_1\times0$、$A\to D\to B$ 的機率為$d_1\times\dfrac{1}{4}$。由此我們可得一開始在$A$執行兩次到達$B$的機率為$b_1\times\dfrac{1}{2}+a_1\times\dfrac{1}{4}+d_1\times\dfrac{1}{4}$，也就是 $b_2=\dfrac{1}{4}\times\dfrac{1}{2}+(\dfrac{1}{2}+0)\times\dfrac{1}{4}=\dfrac{1}{4}$。同理可得$c_2=\dfrac{1}{4}$。從這裡，我們可以看出 $b_{k+1},c_{k+1}$ 需符合關係式 $b_{k+1}=b_k\times\dfrac{1}{2}+(a_k+d_k)\times\dfrac{1}{4}$ 以及 $c_{k+1}=c_k\times\dfrac{1}{2}+(a_k+d_k)\times\dfrac{1}{4}$。也因此若 $b_k=c_k$，自然可得 $b_{k+1}=c_{k+1}$，也因此證得了$b_n=c_n$，對任何正整數 $n$ 皆成立（即選項(4)正確）。若注意到 $b_1=b_2=\dfrac{1}{4}$ 以及 $c_1=c_2=\dfrac{1}{4}$，我們也可以利用上面這兩個關係式，由歸納假設 $b_k=c_k=\dfrac{1}{4}$ 推得 $b_{k+1}=c_{k+1}=\dfrac{1}{4}$。這是因為 $a_k+b_k+c_k+d_k=1$所以由$b_k=c_k=\dfrac{1}{4}$的假設可得$a_k+d_k=\dfrac{1}{2}$。因此由 $b_{k+1}=b_k\times\dfrac{1}{2}+(a_k+d_k)\times\dfrac{1}{4}$ 可得 $b_{k+1}=\dfrac{1}{4}\times\dfrac{1}{2}+\dfrac{1}{2}\times\dfrac{1}{4}=\dfrac{1}{4}$。也因此證得對所有正整數 $n$ 皆會有 $b_n=c_n=\dfrac{1}{4}$。同時得知 $a_n+d_n=\dfrac{1}{2}$，因此選項(5)是錯誤的。
其實若針對選項(5)，也可由 $a_1+d_1=a_2+d_2=\dfrac{1}{2}$，利用歸納假設 $a_k+d_k=\dfrac{1}{2}$（此時 $b_k+c_k=\dfrac{1}{2}$也成立），證得 $a_n+d_n=\dfrac{1}{2}$ （以及 $b_n+c_n=\dfrac{1}{2}$）對所有正整數 $n$ 皆成立。整體來說能證得$a_n+d_n=b_n+c_n=\dfrac{1}{2}$，是了解這些數列重要的步驟。因為由 $b_n+c_n=\dfrac{1}{2}$，以及 $a_{n+1}=a_n\times\dfrac{1}{2}+(b_n+c_n)\times\dfrac{1}{4}$ 可得 $a_{n+1}=\dfrac{1}{2} a_n+\dfrac{1}{8}$ 這個一階的遞迴關係式，即 $a_{n+1}-\dfrac{1}{4}=\dfrac{1}{2}(a_n-\dfrac{1}{4})$。也因此得 $a_{n+1}-\dfrac{1}{4}=(\dfrac{1}{2})^n(a_1-\dfrac{1}{4})$。同理 $b_n,c_n,d_n$ 都符合同樣的遞迴關係式，所以我們可以由 $a_1=\dfrac{1}{2}$, $b_1=c_1=\dfrac{1}{4}$, $d_1=0$，求得 $a_{n+1}=\dfrac{1}{4}(1+\dfrac{1}{2^n})$, $b_n=c_n=\dfrac{1}{4}$ 以及 $d_{n+1}=\dfrac{1}{4}(1-\dfrac{1}{2^n})$。
第14題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 23 | 52 | 2 | 61 | 35 | 15 | 5 | 1 | 50 | 26 | 20 | 10 | 4 |
此題前$33\%$的高分組答對率只有$52\%$，連前$20\%$的最高分組，也才$61\%$，實在令人訝異。而這樣的題目，後$33\%$的低分組得分率僅$2\%$更令人擔憂。拿這一題出來談，就為了讓對這類比率問題有困難的學生提供一些建議。這類比率問題一般來說可以先設總人數為$T$，接著就是算人頭（計算人數）的問題了。不過若學生對符號操作不熟悉的話，對這類純粹比率的問題可以直接設總人數是一個好算數字來處理。因為這題各類只有比率關係，這樣代特定數字的方法不會有問題。這樣處理的方式，沒有觀念偏差的問題，不過切記，若問題中夾雜不是比率的條件（例如某一類比另一類多了5人），就不能直接代數字，只能回歸到用$T$來處理了。
這種分類比率的問題，大部分都會畫一下文氏圖，這樣較好利用取捨（排容）原理處理。用數字來處理的好處，就是學生可以把人數填入文氏圖中，不會搞混。為了方便計算，這一題就直接設全校有10人好了（若後面遇到有小數，則再回來調數字或直接用小數處理也沒關係）。依題意，這10人中有3人僅考數A。而考數A的人中有$\dfrac{5}{8}$同時報考數B，所以剛才僅考數A的3人占全體考數A的$\dfrac{3}{8}$（這是本題唯一的考點），也就是說有報考數A的人共8人。全校10人中剩下的2人就是僅報考數B的人數，再加上報考數A的8人中有$\dfrac{5}{8}$（即5人）同時報考數B，所以報考數B的共有7人。因此得僅報考數B的2人佔所有報考數B的7人中的$\dfrac{2}{7}$。看看以上做法，對於那些覺得比率關係複雜而放棄作答本題的考生實在很可惜。
第15題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 28 | 69 | 1 | 83 | 40 | 12 | 2 | 0 | 68 | 43 | 28 | 10 | 2 |
此題對於向量熟悉的學生，畫一下示意圖，就可以馬上算出答案。對於向量符號操作不熟悉的學生，我一直鼓勵這類線性組合問題，只要不牽涉內積和面積，都可以直接設坐標來做。由於兩不平行向量的線性組合的唯一性，這樣的方法沒有觀念偏差的問題，而且有了具體向量坐標，學生應該比較會操作。
首先依題意我們就先設$\overset{\displaystyle{\rightharpoonup}}{P_1Q_1}=(1,0)$, $\overset{\displaystyle{\rightharpoonup}}{P_2Q_2}=(0,1)$。依此再由題設可得 $\overset{\displaystyle{\rightharpoonup}}{P_1R}=(4,0)$, $\overset{\displaystyle{\rightharpoonup}}{P_2R}=(0,7)$。接下來就是本題的評量重點，如何將這些向量連接成向量 $\overset{\displaystyle{\rightharpoonup}}{Q_1Q_2}$。因為要從$Q_1$出發，我們可先考慮 $\overset{\displaystyle{\rightharpoonup}}{Q_1P_1}$。接著$P_1$為起點的$\overset{\displaystyle{\rightharpoonup}}{P_1R}$，再接以$R$為起點的$\overset{\displaystyle{\rightharpoonup}}{RP_2}$，最後再接$\overset{\displaystyle{\rightharpoonup}}{P_2Q_2}$就可以了。所以我們有\[\overset{\displaystyle{\rightharpoonup}}{Q_1Q_2}=\overset{\displaystyle{\rightharpoonup}}{Q_1P_1}+\overset{\displaystyle{\rightharpoonup}}{P_1R}+\overset{\displaystyle{\rightharpoonup}}{RP_2}+\overset{\displaystyle{\rightharpoonup}}{P_2Q_2}=-(1,0)+(4,0)-(0,7)+(0,1)=(3,-6).\]也就是說 $\overset{\displaystyle{\rightharpoonup}}{Q_1Q_2}= 3\overset{\displaystyle{\rightharpoonup}}{P_1Q_1}-6\overset{\displaystyle{\rightharpoonup}}{P_2Q_2}$。
第17題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 0 | 5 | 0 | 0 | 0 | 0 | 3 | 5 | 0 | 0 | 0 |
大考很常問到有關三個數字所形成的等差數列或等比數列的問題（112年數B第14題就是一例，也是排列組合問題，當時答對率$38\%$）。這類問題若從等差中項或等比中項著手，大多較容易掌握這些數列。本題中由於三角形內角和為$180^\circ$，所以馬上知道這些三角形三內角的中間項為$60^\circ$。也因此，我們可以知道這些三角形有哪幾種，然後再依每一種計算有多少擺放的方式，就可以算出總共有76個。這裡我們為了強調利用等差中項的算法，就不用前述的分類方式，直接算出有幾個三角形。
我們的算法是直接算任取三點其中有一個角是$60^\circ$的三角形共有幾個。 由於三角形三內角和為$180^\circ$，只要有一個角是$60^\circ$，那這個三角形的三內角就符合題目三內角成等差數列的要求。 我們考慮將此$60^\circ$角置於12點位置的情況。所以這個角對應到圓周上間隔為4的兩點，即 1和5、2和6、$\dots$ 一直到 7和11， 這7種情況。因此知，決定將$60^\circ$放在那一點後，每次都有7種方法，所以總共有 $7\times 12=84$種放法。 不過要注意，題目是問會有幾種三角形。剛剛的放法中，當不是正三角形時，由於只有一個角是$60^\circ$，所以這些三角形都不會被重複計算。唯有正三角形時，例如頂點在 12,4,8這三種情況都是同一個正三角形。也就是說剛才的算法裡正三角形總共被算了12次，但實際上只有4個，因此最後要扣掉多算的8個，答案為 $84-8=76$。
這一題應該算很簡單的空間概念題。低分組的考生在此題表現不錯，有全卷第二高的答對率，反而是高分組的答對率還比第2題的答對率低。第18題的答對率，大考中心提供的分組資料如下：
| P | Ph | Pl | Pa | Pb | Pc | Pd | Pe | D | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 64 | 84 | 40 | 88 | 77 | 69 | 56 | 32 | 44 | 11 | 8 | 13 | 24 |
這一題若能善用$\triangle BCD$是等腰三角形，就能馬上求出其面積。不過可能是放在空間中，很多考生顯然沒看出來，而用餘弦算角度再求面積、或是套用海龍公式。當然這都沒問題，只是增加了複雜度，提高了計算錯誤的風險。很好奇，若只是單純的平面上的三角形，答題狀況會不會好很多。在閱卷時，也發現一些令人啼笑皆非的情況，有考生竟然認為$\triangle BCD$面積等於$\triangle ABC$、$\triangle ABD$、$\triangle ACD$三個三角形的面積和。沒錯，示意圖上看起來確實如此，不過老師會想到學生有這個看法，而特別提醒這是錯誤的嗎？這也讓人深刻體會，教導學生正確的空間概念之難處。
求$\overline{AD}$應該是本題組最難的部分。若求出$\overline{AD}$，依題目的取向，應是建議用兩種看法處理四面體$ABCD$的體積。 若看出$\overline{AD}$與平面$ABC$垂直，就可以用以$\triangle ABC$為底的看法求出體積。再利用以$\triangle BCD$為底的看法以及前一題$\triangle BCD$的面積，求出$A$到此底面的高。不過若考生無法求出$\overline{AD}$，即使知道後面的步驟，大多後面的部分就留下空白，以致於整題都無法得分。在此建議老師鼓勵學生在這種情況，不妨寫下後面的步驟，或許還能得到一些分數。這也是需要手寫題的用意。
求$\overline{AD}$難在它需要$\overline{AB}$或$\overline{AC}$來幫忙。這裡基本上就要用到直角三角形$\triangle ADB$和$\triangle ADC$是全等的，得到$\triangle ABC$是等腰直角三角形解出。這部分過程較多，也請學生將過程寫出來，如此即使計算錯誤也能得到一些分數。
知道$\overline{AD}$、$\overline{AB}$以及$\overline{AC}$後，也有考生就利用坐標處理（應該是修習數A的考生）。寫下平面$BCD$方程式後就可以直接利用點與平面距離公式求出$A$到底面$\triangle BCD$的高。這樣的作法，當然不需知道四面體$ABCD$的體積。不過題目不是只要求高，所以請不要忘記還是得回去求四面體$ABCD$的體積，才能得到完整的分數。