

下一頁: Systems of Linear Equations
上一頁: Vectors
前一頁: Inner Product
在本章中我們將大家熟悉
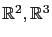 上的向量加法, 係數積, 內積等運算推廣至
上的向量加法, 係數積, 內積等運算推廣至
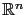 上.
這些推廣而得的運算與
上.
這些推廣而得的運算與
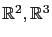 上的運算有共同的性質.
直接利用這些性質而不必利用這些運算的定義, 我們就可以得到許多和
上的運算有共同的性質.
直接利用這些性質而不必利用這些運算的定義, 我們就可以得到許多和
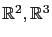 相類似的結果. 換言之, 只要有這些運算性質,
即使更抽象的空間,
有些事情我們依然可以如平面或空間一樣的情形``看到''.
希望大家能體會到這些運算性質的重要性,
將來我們就是要利用這些性質進入較抽象的線性代數世界.
相類似的結果. 換言之, 只要有這些運算性質,
即使更抽象的空間,
有些事情我們依然可以如平面或空間一樣的情形``看到''.
希望大家能體會到這些運算性質的重要性,
將來我們就是要利用這些性質進入較抽象的線性代數世界.
Cellist
2010-12-08