首先我們回顧在
![]() 和
和
![]() 中內積的定義. 若在
中內積的定義. 若在
![]() 中
中
![]() , 則
, 則
![]() 的內積
的內積
![]() 定義成
定義成
![]() . 而在
. 而在
![]() 中若
中若
![]() , 則
, 則
![]() 的內積
的內積
![]() 定義成
定義成
![]() 由這定義我們很自然地可推廣到
由這定義我們很自然地可推廣到
![]() 中向量的內積如下:
中向量的內積如下:
向量的內積和向量的運算有一定的關係, 以下就是它們之間的關係
假設
![]() .
我們想利用
.
我們想利用 ![]() (summation) 這個符號來處理內積,
讓大家習慣這個便利的符號.
(summation) 這個符號來處理內積,
讓大家習慣這個便利的符號.
(1) 依定義
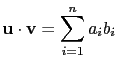
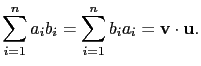
(2) 依定義
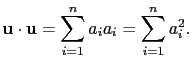
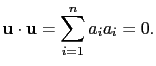
(3)
![]() 這個符號表示
這個符號表示
![]() 這個向量與
這個向量與
![]() 的內積, 因
的內積, 因
![]() 故由定義知
故由定義知
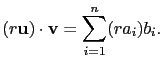
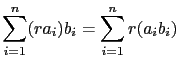
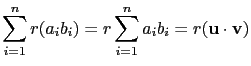
(4)
![]() 這個符號表示
這個符號表示
![]() 這個向量與
這個向量與
![]() 的內積, 因
的內積, 因
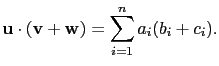
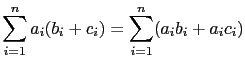
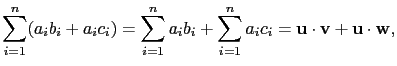
Proposition 1.4.2 (2) 告訴我們除了零向量
![]() 以外其餘向量
以外其餘向量
![]() 皆需符合
皆需符合
![]() ,
所以很自然地我們可依此定義向量的長度.
,
所以很自然地我們可依此定義向量的長度.
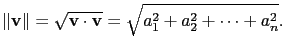
我們可以利用 Proposition 1.4.2 的處理一些有關於內積的性質, 而不必涉及內積的定義.
再次強調一次 Lemma 1.4.4 僅用到內積的性質, 所以在一般的情形若我們不是利用 Definition 1.4.1 的方法定義內積 (當然此時長度的定義也跟著改變) 但所定義的內積仍保有 Proposition 1.4.2 中的性質, 我們依然可得到 Lemma 1.4.4 中的性質. Lemma 1.4.4 最常見的就是可以幫助我們推得所謂的「柯希、舒瓦茲」不等式.
若
![]() 皆不為零向量, 考慮
皆不為零向量, 考慮
![]() 且
且
![]() . 此時
. 此時
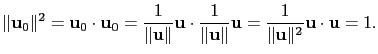
從上可知當
![]() 皆不為零向量時,
此不等式之等式會成立等同於
皆不為零向量時,
此不等式之等式會成立等同於
![]() 或
或
![]() . 此時由式子 (1.6) 分別得
. 此時由式子 (1.6) 分別得
![]() 或
或
![]() , 也就是說
, 也就是說
![]() 或
或
![]() . 換回
. 換回
![]() 我們得
我們得
![]() 或
或
![]() . 這分別表示
. 這分別表示
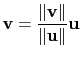 或
或 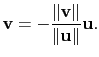
反之若
![]() , 則由 Proposition 1.4.2 可得
, 則由 Proposition 1.4.2 可得
利用內積我們可以知道坐標平面或空間中向量之間的一些幾何關係.
例如若兩非零向量
![]() 的夾角為
的夾角為 ![]() , 因為
, 因為
![]() ,
所以我們可以利用內積得知此二非零向量所夾角度. 特別地當
,
所以我們可以利用內積得知此二非零向量所夾角度. 特別地當
![]() 即表示
即表示
![]() 和
和
![]() 垂直.
我們也可將此幾何意義推廣到更一般的
垂直.
我們也可將此幾何意義推廣到更一般的
![]() . 雖然當
. 雖然當 ![]() 時,
我們無法``看到''
時,
我們無法``看到''
![]() 中的向量 (無法用幾何的方式來定義夾角),
此時我們可以沿襲
中的向量 (無法用幾何的方式來定義夾角),
此時我們可以沿襲
![]() 上的結果定義兩非零向量
上的結果定義兩非零向量
![]() 的夾角為
的夾角為 ![]() , 其中
, 其中
![]() 使得
使得
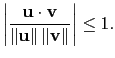
注意這裡因在
![]() 空間, 習慣上垂直我們稱為 orthogonal
而不用大家一般幾何上常用的 perpendicular. 有了垂直概念後,
我們也可以將
空間, 習慣上垂直我們稱為 orthogonal
而不用大家一般幾何上常用的 perpendicular. 有了垂直概念後,
我們也可以將
![]() 或
或
![]() 上的向量在另一向量上的投影
(projection) 之概念推廣至
上的向量在另一向量上的投影
(projection) 之概念推廣至
![]() .
.
我們先看
![]() 的情況, 給定一非零向量
的情況, 給定一非零向量
![]() , 對任意
, 對任意
![]() , 若
, 若
![]() 為
為
![]() 在
在
![]() 上的投影,
表示向量
上的投影,
表示向量
![]() (參考下圖虛線表示的向量) 會和
(參考下圖虛線表示的向量) 會和
![]() 垂直, 即
垂直, 即
![]() , 也就是說
, 也就是說
![]() .
.
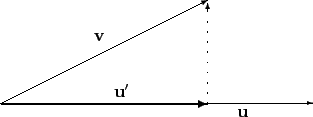
Proposition 1.4.7, 大致上是說給定一
![]() 中的非零向量
中的非零向量
![]() 後, 我們都可以將
後, 我們都可以將
![]() 中任一向量
中任一向量
![]() 分解成兩個向量之和, 其中一個向量與
分解成兩個向量之和, 其中一個向量與
![]() 平行 (即定理中的
平行 (即定理中的
![]() ) 而另一個與
) 而另一個與
![]() 垂直 (即定理中的
垂直 (即定理中的
![]() ),
且這個表法是唯一的. 我們稱與
),
且這個表法是唯一的. 我們稱與
![]() 平行的那個向量
平行的那個向量