(1) ![]() 的圓心坐標為 (5, 0)
的圓心坐標為 (5, 0)
(2) ![]() 上的點與直線
L : 3x + 4y - 15 = 0 的最遠距離等於4
上的點與直線
L : 3x + 4y - 15 = 0 的最遠距離等於4
(3) 直線
L1 : 3x + 4y + 15 = 0 與 ![]() 相切
相切
(4) ![]() 上恰有兩個點與直線
L2 : 3x + 4y = 0 的距離等於2
上恰有兩個點與直線
L2 : 3x + 4y = 0 的距離等於2
(5) ![]() 上恰有四個點與直線
L3 : 3x + 4y - 5 = 0 的距離等於2
上恰有四個點與直線
L3 : 3x + 4y - 5 = 0 的距離等於2
說明:這一題主要問的是平面中圓上的點和直線的距離,
是為了評量是否了解圓與直線的關係. 事實上若知道如何求點和直線的距離,
處理此題應沒有什麼大問題.
要處理圓和直線的距離,
基本上只要找到圓心及半徑再求出圓心與直線的距離就可以了.
也就是說若圓心與直線的距離小於半徑, 則此圓和此直線相交於相異兩點;
若圓心與直線的距離等於半徑, 則此圓和此直線相切;
而若圓心與直線的最短大於半徑, 則此圓和此直線不相交. 此題中圓
![]() 的方程式經由配方可化為
(x - 5)2 + y2 = 42, 故知
的方程式經由配方可化為
(x - 5)2 + y2 = 42, 故知 ![]() 的圓心為 (5, 0) 而半徑是 4. 題目中雖涉及了好幾條直線,
不過它們都互相平行, 方程式皆為 3x + 4y + d = 0 這樣的形式. 大家都應知道
(5, 0) 到 3x + 4y + d = 0 的距離為
的圓心為 (5, 0) 而半徑是 4. 題目中雖涉及了好幾條直線,
不過它們都互相平行, 方程式皆為 3x + 4y + d = 0 這樣的形式. 大家都應知道
(5, 0) 到 3x + 4y + d = 0 的距離為
![]() 15 + d
15 + d![]() /5.
/5.
首先我們看看各選項中的直線和圓 ![]() 之間的相關位置. 選項 (2)
的直線
L : 3x + 4y - 15 = 0 通過
之間的相關位置. 選項 (2)
的直線
L : 3x + 4y - 15 = 0 通過 ![]() 的圓心 (5, 0)
(你可能不會這麼聰明發現 (5, 0) 在 L 上, 不過代 d = - 15
入上面所提圓心到直線距離的式子, 不難得到圓心到 L 的距離是 0).
選項 (3) 的直線
L1 : 3x + 4y + 15 = 0 和
的圓心 (5, 0)
(你可能不會這麼聰明發現 (5, 0) 在 L 上, 不過代 d = - 15
入上面所提圓心到直線距離的式子, 不難得到圓心到 L 的距離是 0).
選項 (3) 的直線
L1 : 3x + 4y + 15 = 0 和 ![]() 的圓心 (5, 0)
的最短距離為 6, 大於
的圓心 (5, 0)
的最短距離為 6, 大於 ![]() 的半徑, 所以不相交. 選項 (4),(5)
的直線 L2, L3 和
的半徑, 所以不相交. 選項 (4),(5)
的直線 L2, L3 和 ![]() 的圓心的最短距離分別為 3 和 2,
皆小於
的圓心的最短距離分別為 3 和 2,
皆小於 ![]() 的半徑, 所以此二直線皆與
的半徑, 所以此二直線皆與 ![]() 相交於兩點.
相交於兩點.
選項 (2), (4), (5) 問的是圓上的點和各直線的距離. 圓上有無窮多點,
我們當然不能一個一個去算距離. 不過我們知道一個點 P 到一直線 L
的距離的算法就是過該點 P 畫一直線使之和 L 垂直, 此直線和 L
的交點 Q 就是所謂 P 點在 L 的``投影點'' (或垂足), 而
![]() 線段長就是 P 點到 L 的距離. 所以我們可以在圓
線段長就是 P 點到 L 的距離. 所以我們可以在圓
![]() 上各點上畫一與 L 垂直(自然也和 L2, L3
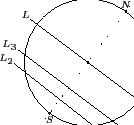
垂直)的直線而得到這一點在 L, L2, L3 的投影點. 現在我們過圓心畫一與
L 垂直的直線, 假設此直線與
上各點上畫一與 L 垂直(自然也和 L2, L3
垂直)的直線而得到這一點在 L, L2, L3 的投影點. 現在我們過圓心畫一與
L 垂直的直線, 假設此直線與 ![]() 交於 N, S 兩點如下圖,
交於 N, S 兩點如下圖,
一般來說當給定一點 P 和一圖形 T, 若遇到問 T 上有多少點和 P
的距離為 d 時, 我們經常處理的方式是先找到所有與 P 點距離為 d
的點, 即以 P 為圓心半徑為 d 的圓, 這個圓和 T 的交點個數就是
T 上和 P 的距離為 d 的點的個數. 這一題,
我們也可用類似的方法處理. 例如選項 (4), 我們可以先找到所有和 L2
距離為 2 的點所成之集合, 再看這些點所成集合和 ![]() 的交點個數即可. 不難發現, 這些點所成的集合事實上是兩條與
L2 平行的直線. 一條 L2' 與
的交點個數即可. 不難發現, 這些點所成的集合事實上是兩條與
L2 平行的直線. 一條 L2' 與 ![]() 的圓心在 L2 的同側,
另一條 L2'' 在另一側. 由於 L2' 和 L2 的距離為 2 且圓心與
L2 的距離是 3, 故知圓心和 L2' 的距離是 1, 故知 L2' 和
的圓心在 L2 的同側,
另一條 L2'' 在另一側. 由於 L2' 和 L2 的距離為 2 且圓心與
L2 的距離是 3, 故知圓心和 L2' 的距離是 1, 故知 L2' 和
![]() 交於兩點. 同理知圓心和 L2'' 的距離是 3 + 2 = 5,
因為此距離大於
交於兩點. 同理知圓心和 L2'' 的距離是 3 + 2 = 5,
因為此距離大於 ![]() 的半徑, 故知 L2'' 和
的半徑, 故知 L2'' 和 ![]() 不相交.
因此知
不相交.
因此知 ![]() 上恰有兩個點與直線 L2 的距離等於 2. 同樣的,
所有和 L3
距離為 2 的點所成之集合是兩條與
L3 平行的直線. 一條 L3' 與
上恰有兩個點與直線 L2 的距離等於 2. 同樣的,
所有和 L3
距離為 2 的點所成之集合是兩條與
L3 平行的直線. 一條 L3' 與 ![]() 的圓心在 L3 的同側,
另一條 L3'' 在另一側. 由於圓心與 L3' 的距離是 2 - 2 = 0, 故知
L3' 和
的圓心在 L3 的同側,
另一條 L3'' 在另一側. 由於圓心與 L3' 的距離是 2 - 2 = 0, 故知
L3' 和 ![]() 交於兩點. 而圓心與 L3'' 的距離是 2 + 2 = 4, 故知
L3' 和
交於兩點. 而圓心與 L3'' 的距離是 2 + 2 = 4, 故知
L3' 和 ![]() 相切 (交於一點). 因此知
相切 (交於一點). 因此知 ![]() 上恰有三個點與直線 L3 的距離等於 2.
上恰有三個點與直線 L3 的距離等於 2.