11

設坐標空間中三條直線 L₁, L₂, L₃ 的方程式分別為

L₁ :     $${\frac{x}{1}}$$ = $${\frac{y+3}{6}}$$ = $${\frac{z+4}{8}}$$;        L₂ :     $${\frac{x}{1}}$$ = $${\frac{y+3}{3}}$$ = $${\frac{z+4}{4}}$$;        L₃ :     $${\frac{x}{1}}$$ = $${\frac{y}{3}}$$ = $${\frac{z}{4}}$$

試問下列哪些選項是正確的？

(1) L₁ 與 L₂ 相交         (2) L₂ 與 L₃ 平行

(3) 點 P(0, - 3, - 4) 與 Q(0, 0, 0) 的距離即為點 P 到 L₃ 的最短距離

(4) 直線 L : 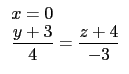$\left\{\vphantom{ \begin{array}{ll} x=0 \\ \displaystyle{\frac{y+3}{4}=\frac{z+4}{-3}}\\ \end{array}%% }\right.$$\begin{array}{ll} x=0 \\ \displaystyle{\frac{y+3}{4}=\frac{z+4}{-3}}\\ \end{array}$ 與直線 L₁, L₂ 皆垂直

(5) 三直線 L₁, L₂, L₃ 共平面

說明:此題考空間中三給定直線的關係. 由於給定的三直線方程式並沒有在數據上刁難同學且沒有歪斜的情況, 此題並不算難. 可能最後一個選項問三線是否共面會讓同學覺得較棘手.

在空間中的直線只要知道通過哪一點且知道方向那麼這條直線就唯一確定了. 此題中依所給的方程式, 我們知 L₁, L₂ 和 L₃ 分別通過了 (0, - 3, - 4), (0, - 3, - 4) 和 (0, 0, 0) 而它們的方向向量分別是 (1, 6, 8), (1, 3, 4) 和 (1, 3, 4). 既然 L₁ 和 L₂ 通過了同一點 (0, - 3, - 4) 所以它們是相交的. L₂ 和 L₃ 雖然有相同的方向向量但這並不表示它們是平行的, 除非能確定它們不是同一條直線. 然而因 x = 0, y = 0, z = 0 並不能滿足 L₂ 的方程式, 這表示 L₂ 並未通過 (0, 0, 0) 這一點. 但 L₃ 通過 (0, 0, 0), 故知 L₂ 和 L₃ 不可能是同一條直線, 而得 L₂ 與 L₃ 平行. 要回答選項 (3) 我們必須知道若 P 是 L₃ 外一點而 Q 在 L₃ 上, 那麼 $\overline{PQ}$ 是 P 到 L₃ 的最短距離若且唯若 $\overrightarrow{PQ}$ 和 L₃ 的方向向量垂直. 此選項中 $\overrightarrow{PQ}$ = (0, 3, 4) 而 L₃ 的方向向量為 (1, 3, 4), 故由 (0, 3, 4) ^. (1, 3, 4) = 9 + 16$\ne$ 0 知此選項是錯的.

回答選項 (4) 要小心! 我們都知道兩直線若垂直則此二直線的方向向量相互垂直, 但是兩個方向向量相互垂直的直線並不一定是垂直的 (有可能歪斜) 除非此二直線相交. 所以處理這一選項時同學不要一看到 L 的方向向量 (0, 4, - 3) 和 L₁, L₂ 的方向向量 (1, 6, 8), (1, 3, 4) 都垂直就馬上認為此選項是對的, 還要檢查一下 L 是否和 L₁ 與 L₂ 相交. 還好出題者沒有存心刁難, 我們很容易看出 L, L₁, L₂ 皆通過 (0, - 3, - 4) 這一點, 所以選項 (4) 是對的.

近年來大考的多選題常常是最後一個選項最難, 而且出題者或多或少會希望能利用前面幾個選項的結果來處理最後一個選項. 這是同學們應注意的. 例如此題的選項 (5) 就可利用前面幾個選項來處理. 我們已知 L₁, L₂ 相交 (不歪斜) 所以此二直線共平面, 再利用 L₂ 與 L₃ 平行, 所以我們只要知道 L₃ 和 L₁ 相交的話, 那麼這三直線就共面了. 利用 L₃ 的參數式 x = t, y = 3t, z = 4t 代入 L₁ 的方程式我們很容易求出 L₁ 和 L₃ 相交於 (1, 3, 4), 所以此三直線共平面. 要注意一般來說 L₁ 和 L₂ 相交且 L₁ 與 L₃ 相交並不保證 L₁, L₂, L₃ 會共平面. 這裡是因為 L₂ 和 L₃ 平行所以共平面. 另外一個看法是由選項 (4) 知道 L₁, L₂ 所共平面 M 的法向量是 (0, 4, - 3), 而選項 (3) 的 P(0, - 3, - 4), Q(0, 0, 0) 分別在 L₂ 和 L₃ 上, 再由 $\overrightarrow{PQ}$ = (0, 3, 4) 與 M 的法向量 (0, 4, - 3) 垂直知 Q 點也在平面 M 上 (因 P 在 L₂ 上故在 M 上) 再由 L₃ 與 L₂ 平行得知 L₃ 上的點皆在 M 上而知此三直線 ( L₁, L₂, L₃) 都在平面 M 上. 要注意一般來說若 L₁ 和 L₂ 所共的平面和 L₃ 相交並不能保證 L₁, L₂, L₃ 會共平面. 這裡是仍然是因為 L₂ 和 L₃ 平行所以會共平面.

前面所提的兩種判斷三直線是否共平面的方法並不適用於一般的情形 (需其中兩直線平行), 在這裡我們還是介紹大家用最基本的方式處理. 首先先將 L₁, L₂ 所共的平面找出 (當然了若 L₁, L₂ 不共面, 即 L₁, L₂ 是歪斜的, 那當然 L₁, L₂, L₃ 就不共面了). 接下來可找出 L₂, L₃ 所共的平面. 如果這兩平面相同, 則 L₁, L₂, L₃ 就共面了 (反之, 自然不共面). 如果你不想再找第二個平面 (即 L₂, L₃ 所共的之平面), 那麼可直接用 L₃ 的參數式來判定 L₃ 是否落在 L₁, L₂ 所共之平面.

如何找出兩直線的共平面呢? 要知道一個平面可由其通過的一點及其法向量來決定. 我們先考慮兩直線不平行的情況來說明, 例如此題的 L₁, L₂ 二直線. 假設 L₁, L₂ 所共的平面為 M. 我們可在 L₁ 上任取一點, 如此題的點 P(0, - 3, - 4). 可知 M 需通過 P 點. 再來因 L₁, L₂ 在 M 上, 所以 M 的法向量必和 L₁, L₂ 的方向向量 (例如此題的 (1, 6, 8),(1, 3, 4)) 垂直. 一般來說我們可用外積或解方程式的方法求出此法向量, 然而由選項 (4) 已知 (0, 4, - 3) 和 (1, 6, 8),(1, 3, 4) 垂直所以 (0, 4, - 3) 是 M 的法向量, 因此得 M 的方程式為 0(x - 0) + 4(y + 3) - 3(z + 4) = 0, 即 4y - 3z = 0. 一般的在尚不知 L₁, L₂ 是否為歪斜的情形, 這樣所得的平面 M 僅知 L₁ 在 M 上, 而由於 M 的法向量和 L₂ 的方向向量垂直, 我們知 L₂ 要不然和 M 不相交 (此時可知 L₁, L₂ 歪斜), 要不然就是完全落在 M 上. 因此我們只要在 L₂ 任取一點看看是否在 M 上就可決定 L₁, L₂ 是否共平面 M. 也就是說, 若所取 L₂ 上的這一點不能滿足 M 的方程式就表示 L₁, L₂ 不共平面; 反之, 若取的這一點滿足 M 的方程式就表示 L₁, L₂ 共同落在 M 這個平面. 然而此題 P(0, - 3, - 4) 也在 L₂ 上, 故知 L₂ 也落在 M 上 (事實上由前面選項 (1) 知 L₁, L₂ 不歪斜, 故可馬上得知 M 是 L₁, L₂ 所共之平面). 接著我們探討兩線平行的情況, 例如此題的 L₂, L₃ 二直線. 假設 L₂, L₃ 所共的平面為 M'. 我們可在 L₃ 上任取一點, 如此題的點 Q(0, 0, 0). 可知 M' 需通過 Q 點. 如何決定 M' 的法向量呢? 基本上只要在平面上找到兩不平行的向量就可以決定法向量. 前面兩直線不平行的情形, 我們就是利用此二直線的方向向量必在所共平面上, 所以用它們決定出法向量. 現在兩直線平行, 我們只有一個方向向量, 如何找到平面上另一個不與之平行的向量呢? 由於依假設 L₂, L₃ 皆在 M' 上, 所以我們可以分別在 L₂, L₃ 上任取一點 (例如此題中的 P(0, - 3, - 4) 和 Q(0, 0, 0)), 那麼這兩點所決定的向量 (例如此題中 $\overrightarrow{PQ}$ = (0, 3, 4)) 就落在 M' 上. 所以我們可利用直線的方向向量和這個向量 (例如此題的 (1, 3, 4) 和 (0, 3, 4)) 得到 M' 的法向量 (例如此題就是 (0, 4, - 3)), 進而得到 M' 的方程式 (例如此題就是 4y - 3z = 0). 既然我們得到 M 和 M' 有相同的方程式 (即同一平面), 所以知 L₁, L₂, L₃ 共平面. 當然我們也可由 L₃ 的參數式 x = t, y = 3t, z = 4t 滿足 M 的方程式 4y - 3z = 0, 而得知 L₃ 也落在 M 上.