C

坐標平面上，以原點 O 為圓心的圓上有三個相異點 A(1, 0), B, C，且 $\overline{AB}$ = $\overline{BC}$。已知銳角三角形 OAB 的面積為 3/10，則 $\vartriangle$OAC 的面積為何？(化為最簡分數)

說明:此題若想到一圓上等長的弦對應相同的圓心角, 就能很輕鬆的利用倍角公式處理. 基本上這種看法是用極坐標的方式看此題, 不過題目用直角坐標表示, 同學可能沒想到此點, 而用較複雜的直角坐標方法處理. 這可能不是出題者的原意, 如果題目 $\overline{AB}$ = $\overline{BC}$ 的條件改為 AB 弧長和 BC 弧長相等, 或許較容易引導同學往角度的方向去想.

此題可以反過來思考. 若先知道 C 點坐標, 當然就可以知道 $\vartriangle$OAC 的面積. 而 C 的位置需利用 $\overline{AB}$ = $\overline{BC}$ 這個條件由 B 點來決定, 而 B 點坐標當然就由 OAB 的面積來確定了. 因為 A, B 皆在以 O 為圓心的單位圓上, 若 $\vartriangle$OAB 以 $\overline{OA}$ 為底, 利用三角形面積公式, 知其高為 3/5. 也就是說 B 點和 x-軸 (底 $\overline{OA}$ 所在直線) 的距離為 3/5 (即 y 坐標的絕對值為 3/5). 因 $\vartriangle$OAB 是銳角三角形, 不失一般性, 我們可假設 B 點坐標為 (4/5, 3/5), 而得 $\overline{AB}$ = $\sqrt{10}$/5. 如何求 C 點呢? 因為 C 點和 B 點的距離也是 $\sqrt{10}$/5, 所以 C 點會落在以 B(4/5, 3/5) 為圓心, $\sqrt{10}$/5 為半徑的圓上. 再利用 C 點也在以原點為圓心的單位圓上, 我們知道 C 點應在兩圓 (x - 4/5)² + (y - 3/5)² = 10/25 和 x² + y² = 1 的交點上. 故解聯立方程式

$$\left\{\vphantom{ \begin{array}{l} (x-\frac{4}{5})^2+(y-\frac{3}{5})^2=\frac{10}{25} \\ x^2+y^2=1\\ \end{array}%% }\right.$$$$\begin{array}{l} (x-\frac{4}{5})^2+(y-\frac{3}{5})^2=\frac{10}{25} \\ x^2+y^2=1\\ \end{array}$$.

解這樣的聯立方程式 (求兩圓交點), 可先展開利用相減消去 x², y² 項, 得 4x + 3y = 4. 再將 x = 1 - (3/4)y 帶回 x² + y² = 1 解得 y = 0 或 y = 24/25. 故知 C 點坐標為 (7/25, 24/25) (y = 0 對應到 A(1, 0)), 而得 $\vartriangle$OAC 的面積為 1/2×1×24/25 = 12/25.

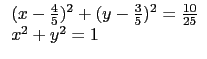若用角度的觀點來看此題就容易多了. 設 $\angle$BOA = $\theta$, 故由(銳角)三角形 OAB 的面積為 3/10 知 3/10 = (1/2)$\overline{OA}$ $\overline{OB}$sin$\theta$, 得 sin$\theta$ = 3/5. 又由 $\overline{AB}$ = $\overline{BC}$ 可得 $\angle$BOA = $\angle$COB, 也就是說 $\angle$COA = 2$\theta$. 故得 $\vartriangle$OAC 的面積為

$${\textstyle\frac{1}{2}}$$$$\overline{OC}$$ $$\overline{OA}$$sin(2$$\theta$$) = sin$$\theta$$cos$$\theta$$ = $${\textstyle\frac{3}{5}}$$×$${\textstyle\frac{4}{5}}$$ = $${\textstyle\frac{12}{25}}$$.