
下一頁: F
上一頁: 三、選填題
前一頁: C
設 O(0, 0, 0) 為坐標空間中某長方體的一個頂點,且知
(2, 2, 1),(2, - 1, - 2),(3, - 6, 6) 為此長方體中與 O 相鄰的三頂點。若平面
E : x + by + cz = d 將此長方體截成兩部分,其中包含頂點 O
的那一部分是個正立方體,則 (b, c, d )= ?
說明:這一題考簡單的空間中的平面方程式,
不過不是純粹的代數問題而需要立體幾何的概念.
立體幾何的概念很多同學都很懼怕, 此題若能有相關的略圖出現,
或許對同學很有幫助.
不過出題者的原意是否就是希望同學們自己能在空間坐標中約略的將相關的點標示出,
就不得而知了.
立體幾何的概念就像前面提的隨機的概念一樣, 很難明確的寫下來.
幾乎要憑你對它的``感覺''. 希望以下的說明你能``感覺得出來''.
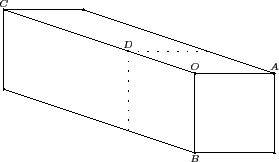
我們用以下的長方體簡圖來說明如何處理這個問題.
這是一個長方體 (希望你能看出來它像一塊長長的豆腐). 頂點 O
有三個相鄰的頂點 A, B, C. 如果我們想在豆腐上切一刀, 使得其中包含 O
的這一部分是一個正方體 (方塊),
那麼當然原來這一塊豆腐需有一面(事實上是兩面) 是正方形才行, 如圖上含
O, A, B 三點的這一面 (即
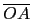 =
= 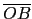 ). 而且 O
和另一相鄰的頂點 C 的連線 (稱為稜邊) 線段長不能小於
). 而且 O
和另一相鄰的頂點 C 的連線 (稱為稜邊) 線段長不能小於
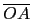 (否則哪能切成正方體?). 當我們要切下時,首先可在
(否則哪能切成正方體?). 當我們要切下時,首先可在
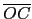 稜邊上選一點 D 使得
稜邊上選一點 D 使得
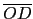 =
= 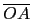 , 然後往 D 點切下去.
切下時``刀面''需與原先是正方形的那一面 (即含 O, A, B 三點的這一面)
相平行, 這樣切下去才會得到一個正方體. 所以我們所要的平面需通過 D
點且其法向量就是原先是正方形的那一平面 (即含 O, A, B 三點的這一平面)
的法向量. 由於這是一個長方體, 向量
, 然後往 D 點切下去.
切下時``刀面''需與原先是正方形的那一面 (即含 O, A, B 三點的這一面)
相平行, 這樣切下去才會得到一個正方體. 所以我們所要的平面需通過 D
點且其法向量就是原先是正方形的那一平面 (即含 O, A, B 三點的這一平面)
的法向量. 由於這是一個長方體, 向量
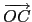 和含
O, A, B 三點的這一平面相垂直, 所以法向量可取向量
和含
O, A, B 三點的這一平面相垂直, 所以法向量可取向量
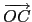 . 所以我們剩下的問題就是如何決定 A, B, C 和 D
點. 由於 O(0, 0, 0) 到
(2, 2, 1),(2, - 1, - 2),(3, - 6, 6) 的距離分別為
3, 3, 9, 所以 O 到 (2, 2, 1) 和 (2, - 1, - 2)
就是比較短且形成正方形的稜邊, 而 O 到 (3, - 6, 6)
就是比較長的稜邊 (要切的邊). 所以對應到上圖, 我們可依次令三點
(2, 2, 1),(2, - 1, - 2),(3, - 6, 6) 為 A, B, C. 故得此平面之法向量為
. 所以我們剩下的問題就是如何決定 A, B, C 和 D
點. 由於 O(0, 0, 0) 到
(2, 2, 1),(2, - 1, - 2),(3, - 6, 6) 的距離分別為
3, 3, 9, 所以 O 到 (2, 2, 1) 和 (2, - 1, - 2)
就是比較短且形成正方形的稜邊, 而 O 到 (3, - 6, 6)
就是比較長的稜邊 (要切的邊). 所以對應到上圖, 我們可依次令三點
(2, 2, 1),(2, - 1, - 2),(3, - 6, 6) 為 A, B, C. 故得此平面之法向量為
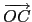 = (3, - 6, 6). 而 D 點坐標應在 O 到 C 的
1/3 處, 故由分點公式可得 D 點坐標為 (1, - 2, 2).
因此得平面方程式為
3(x - 1) - 6(y + 2) + 6(z - 2) = 0, 化簡得 x - 2y + 2z = 9.
當然也可以不求出 D 點, 先利用法向量求出平面方程式為
x - 2y + 2z - d = 0
再利用點 O 到平面的距離應為 3, 得到 d = ±9. 然而當 d = 9
時才會使 O(0, 0, 0) 和 C(3, - 6, 6) 落於平面的相異兩側 (因為分別將
x = 0, y = 0, z = 0 和
x = 3, y = - 6, z = 6 代入 x - 2y + 2z - 9 會異號而代入
x - 2y + 2z + 9 會同號), 所以確認此平面方程式為 x - 2y + 2z = 9.
= (3, - 6, 6). 而 D 點坐標應在 O 到 C 的
1/3 處, 故由分點公式可得 D 點坐標為 (1, - 2, 2).
因此得平面方程式為
3(x - 1) - 6(y + 2) + 6(z - 2) = 0, 化簡得 x - 2y + 2z = 9.
當然也可以不求出 D 點, 先利用法向量求出平面方程式為
x - 2y + 2z - d = 0
再利用點 O 到平面的距離應為 3, 得到 d = ±9. 然而當 d = 9
時才會使 O(0, 0, 0) 和 C(3, - 6, 6) 落於平面的相異兩側 (因為分別將
x = 0, y = 0, z = 0 和
x = 3, y = - 6, z = 6 代入 x - 2y + 2z - 9 會異號而代入
x - 2y + 2z + 9 會同號), 所以確認此平面方程式為 x - 2y + 2z = 9.


下一頁: F
上一頁: 三、選填題
前一頁: C
Li
2008-03-06