F

設 a, b 為正整數。若 b² = 9a，且 a + 2b > 280，則 a 的最小可能值為何？

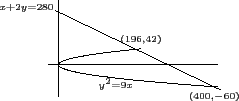
說明:這是一個拋物線上的格子點問題, 牽涉到二次多項式的因式分解以及整數的完全平方概念. 可能出題者為了避免同學們用代的方式求解, 所牽涉的二次多項式係數有點大, 可能分解不易, 不過若考慮到整數完全平方的性質, 所牽涉的係數會小的多.

我們先用坐標幾何的看法來處理, 此題中 (a, b) 是正整數滿足 b² = 9a 表示 (a, b) 這一點需在拋物線 y² = 9x 上. 而 a + 2b > 280 表示 (a, b) 這一點需在直線 x + 2y - 280 = 0 的右側. 首先我們求這個拋物線和直線的交點. 將 x = 280 - 2y 代入 y² = 9x 得 y² + 18y - (60×42) = 0. 故得交點為 (196, 42) 和 (400, - 60). 我們有以下的圖形.

由於題目要求 a, b 皆為正整數, 所以我們需找的拋物線上的點需在第一象限且在 x + 2y - 280 = 0 的右側, 也就是 x 坐標 (即 a 值) 需大於 196. 由於我們要找的是正整數 a 最小的可能值, 或許同學們會認為 a 應為 197. 不過當 a = 197 時, 9a = 9×197 不是一個完全平方, 亦即沒有正整數 b 會滿足 b² = 9×197. 因為 9 = 3², 所以要找到正整數 a 使得 9a 是完全平方, 非得要 a 本身也是完全平方. 所以我們要找的是大於 196 = 14² 的最小的完全平方, 即 15² = 225.

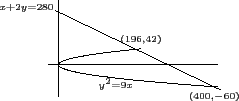
本題也可以用更代數一點的方式處理. 也就是直接用 b² = 9a 代入 a + 2b > 280 來解不等式. 一般來說, 因為在 b² = 9a 中 a 僅有一次, 我們會用 a = b²/9 代入 a + 2b > 280 得到 b 的二次不等式再解之. 這樣處理法並無不可, 只是牽涉的二次式就是前面求交點時所得的二次式, 係數較大, 分解不易. 如果此時我們將 a, b 皆為正整數列入考慮, 即由 b² = 9a, 知道 a 必為一完全平方, 所以可先假設 a = n². 此時得 b = 3n, 代入 a + 2b > 280 可得 n² + 6n - 280 > 0. 這樣不但處理的係數比較小, 而且當我們解不等式得 (n + 20)(n - 14) > 0, 即 n < - 20 或 n > 14, 馬上知 n 取 15, 即 a = 15² 會是最小值.